人教版八年级数学下册 17.1 勾股定理 同步训练(含答案)
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理 同步训练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 385.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 20:03:53 | ||
图片预览


文档简介
17.1 勾股定理 同步训练
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列各组数中,是勾股数的是( )
A.1,2,3 B.4,5,6 C.6,8,9 D.7,24,25
2.如图,一根垂直于地面的旗杆在离地面5m的B处撕裂折断,旗杆顶部落在离旗杆底部12m的A处,则旗杆折断部分AB的高度是( )
A.5m B.12m C.13m D.18m
3.如图,字母B所代表的正方形的面积是( )
A.194 B.144 C.13 D.12
4.如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为( )
A. B. C. D.2
5.如图,在中,,,过点作,交于点,若,则的长度为( )
A. B. C. D.
6.若直角三角形的两直角边长分别为a,b,且满足,则该直角三角形的第三边长的平方为( )
A. B.7 C.或7 D.或
7.如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( )
A. B. C. D.
8.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
9.设直角三角形的较长直角边长为x,较短直角边长为y.若 xy=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
10.如图,在中,,,点在上,,,则的长为( )
A. B. C. D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.已知直角三角形的两边长分别为3、4.则第三边长为________.
12.在△ABC中,∠C=90°,AB=5,则AB2+AC2+BC2=_____.
13.如图,某自动感应门的正上方A处装着一个感应器,离地面的高度AB为2.5米,一名学生站在C处时,感应门自动打开了,此时这名学生离感应门的距离BC为1.2米,头顶离感应器的距离AD为1.5米,则这名学生身高CD为 _____米.
14.在中,若两直角边,满足,则斜边的长度是______.
15.如图,在RtABC中,∠ACB=90°,AB=13,BC=12,分别以点B和点C为圆心、大于BC的长为半径作弧,两弧相交于E,F两点,作直线EF交AB于点D,连接CD,则ACD的周长是_____.
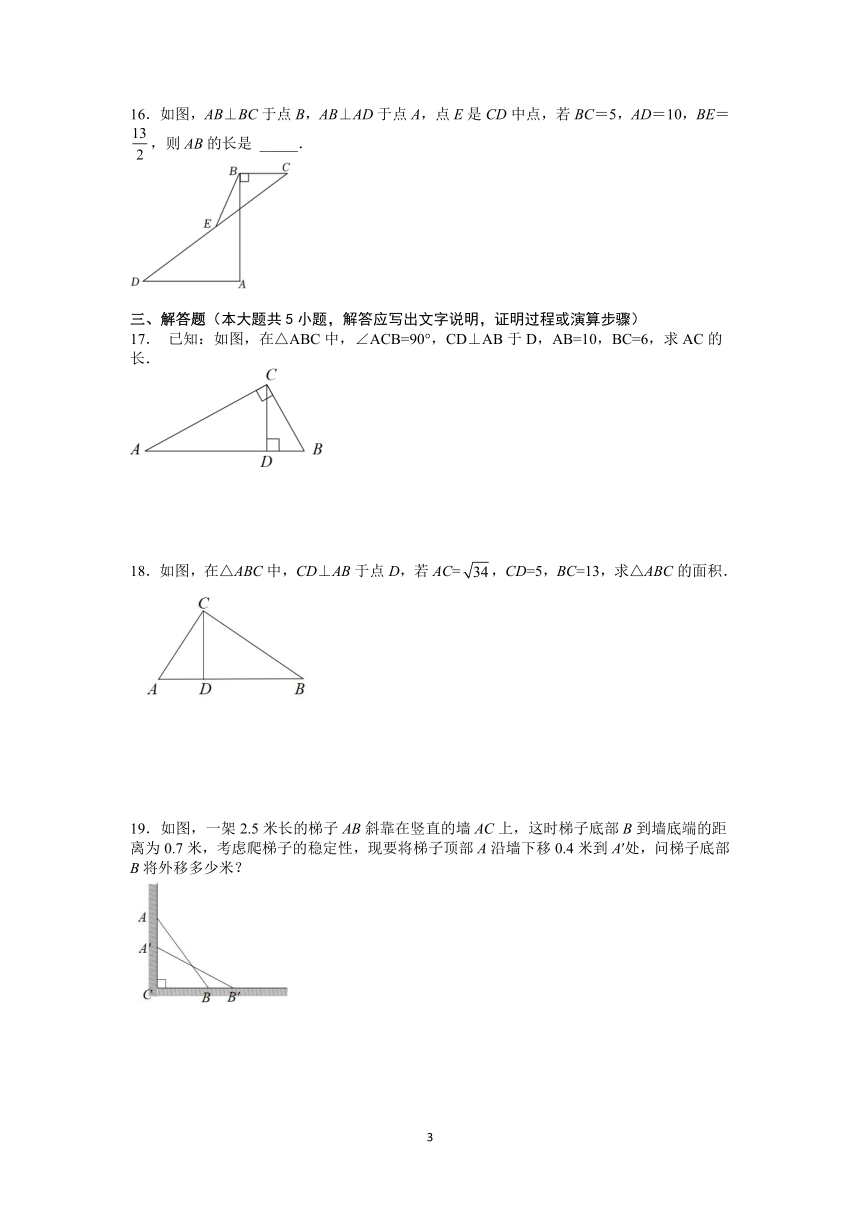
16.如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE=,则AB的长是 _____.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17. 已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AB=10,BC=6,求AC的长.
18.如图,在△ABC中,CD⊥AB于点D,若AC=,CD=5,BC=13,求△ABC的面积.
19.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A′处,问梯子底部B将外移多少米?
20.如图,,,.
(1)求证:≌.
(2)若,,,求的长.
21.如图,在中,,垂足为,,延长至,使得,连接.
(1)求证:;
(2)若,,求的周长和面积.
答案:
1.D 2.C 3.B 4.A 5.B 6.A 7.D. 8.A 9.D 10.D
11.5或 12.50 13.1.6 14.13 15.18 16.12
17.解:△ABC中,∠ACB=90°
AB=10,BC=6
18.解:∵CD⊥AB,
∴∠CDA=∠BDC=90°
在Rt△ADC中,AD2=AC2﹣CD2,在Rt△BCD中,BD2=BC2﹣CD2,
∵AC= ,CD=5,BC=13,
∴AD==3,BD==12,
∴AB=15,
∴S△ABC=AB CD=.
19.解:在Rt△ABC中,∵AB=2.5米,BC=0.7米,
∴米,
又∵AA′=0.4米,
∴A′C=2.4-0.4=2米,
在Rt△A′B′C中,米,
则BB′=CB′-CB=1.5-0.7=0.8米.
故:梯子底部B外移0.8米.
20.(1)证明:∵,
∴,
∴.
在与中,
,
∴≌;
(2)解:∵≌,
∴,
∵,,
∴.
21.(1)证明:,
,
在和中,,
,
;
(2),,
,
,
,
,
,
,
,
,
,
则的周长为,
的面积为.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列各组数中,是勾股数的是( )
A.1,2,3 B.4,5,6 C.6,8,9 D.7,24,25
2.如图,一根垂直于地面的旗杆在离地面5m的B处撕裂折断,旗杆顶部落在离旗杆底部12m的A处,则旗杆折断部分AB的高度是( )
A.5m B.12m C.13m D.18m
3.如图,字母B所代表的正方形的面积是( )
A.194 B.144 C.13 D.12
4.如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为( )
A. B. C. D.2
5.如图,在中,,,过点作,交于点,若,则的长度为( )
A. B. C. D.
6.若直角三角形的两直角边长分别为a,b,且满足,则该直角三角形的第三边长的平方为( )
A. B.7 C.或7 D.或
7.如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( )
A. B. C. D.
8.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
9.设直角三角形的较长直角边长为x,较短直角边长为y.若 xy=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
10.如图,在中,,,点在上,,,则的长为( )
A. B. C. D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.已知直角三角形的两边长分别为3、4.则第三边长为________.
12.在△ABC中,∠C=90°,AB=5,则AB2+AC2+BC2=_____.
13.如图,某自动感应门的正上方A处装着一个感应器,离地面的高度AB为2.5米,一名学生站在C处时,感应门自动打开了,此时这名学生离感应门的距离BC为1.2米,头顶离感应器的距离AD为1.5米,则这名学生身高CD为 _____米.
14.在中,若两直角边,满足,则斜边的长度是______.
15.如图,在RtABC中,∠ACB=90°,AB=13,BC=12,分别以点B和点C为圆心、大于BC的长为半径作弧,两弧相交于E,F两点,作直线EF交AB于点D,连接CD,则ACD的周长是_____.
16.如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE=,则AB的长是 _____.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17. 已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AB=10,BC=6,求AC的长.
18.如图,在△ABC中,CD⊥AB于点D,若AC=,CD=5,BC=13,求△ABC的面积.
19.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A′处,问梯子底部B将外移多少米?
20.如图,,,.
(1)求证:≌.
(2)若,,,求的长.
21.如图,在中,,垂足为,,延长至,使得,连接.
(1)求证:;
(2)若,,求的周长和面积.
答案:
1.D 2.C 3.B 4.A 5.B 6.A 7.D. 8.A 9.D 10.D
11.5或 12.50 13.1.6 14.13 15.18 16.12
17.解:△ABC中,∠ACB=90°
AB=10,BC=6
18.解:∵CD⊥AB,
∴∠CDA=∠BDC=90°
在Rt△ADC中,AD2=AC2﹣CD2,在Rt△BCD中,BD2=BC2﹣CD2,
∵AC= ,CD=5,BC=13,
∴AD==3,BD==12,
∴AB=15,
∴S△ABC=AB CD=.
19.解:在Rt△ABC中,∵AB=2.5米,BC=0.7米,
∴米,
又∵AA′=0.4米,
∴A′C=2.4-0.4=2米,
在Rt△A′B′C中,米,
则BB′=CB′-CB=1.5-0.7=0.8米.
故:梯子底部B外移0.8米.
20.(1)证明:∵,
∴,
∴.
在与中,
,
∴≌;
(2)解:∵≌,
∴,
∵,,
∴.
21.(1)证明:,
,
在和中,,
,
;
(2),,
,
,
,
,
,
,
,
,
,
则的周长为,
的面积为.
