二元一次方程组的解法之代入法[上学期]
图片预览





文档简介
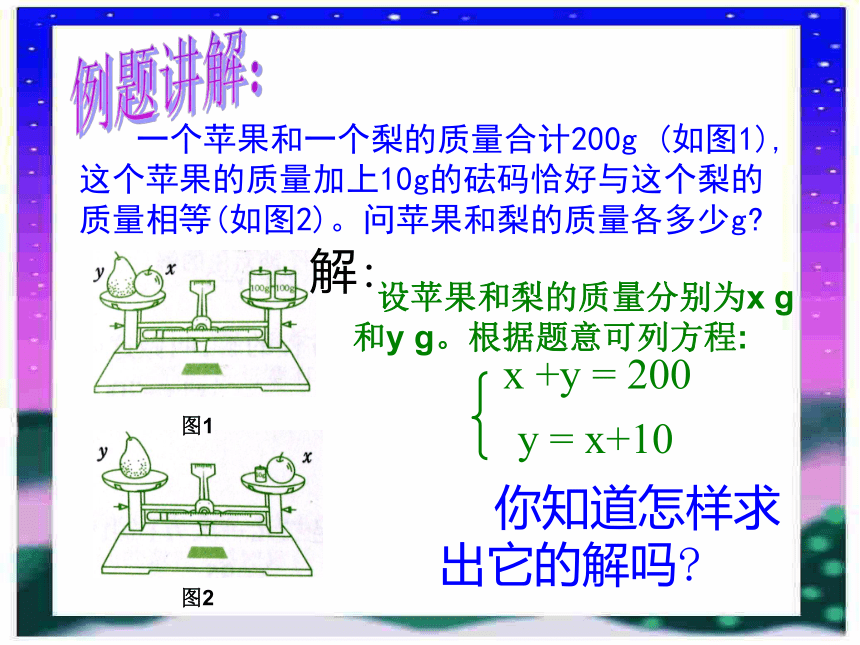
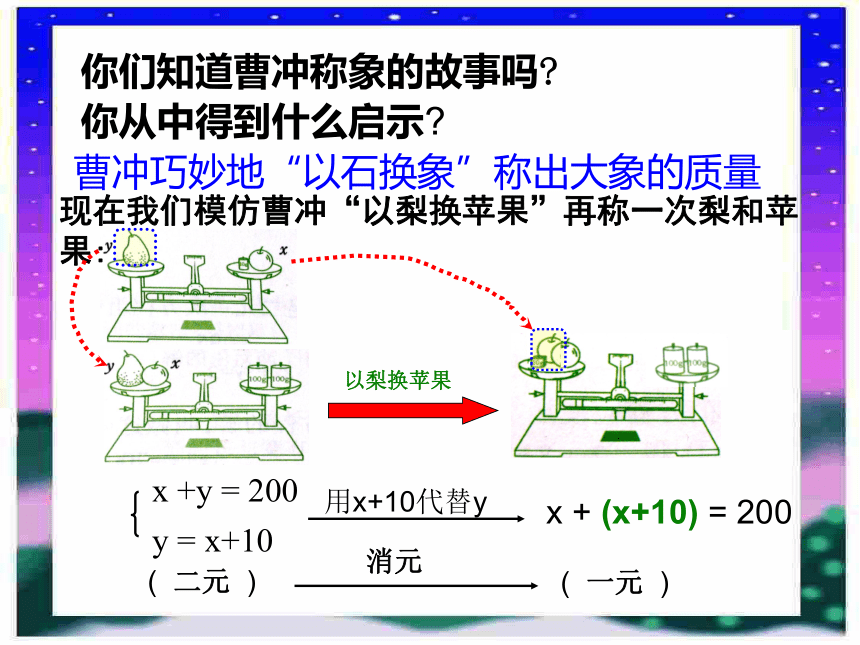
课件18张PPT。回顾复习1.什么是二元一次方程组? 由两个一次方程组成,并且含有两个未知数的方程组, 叫做二元一次方程组。回顾复习2.什么是二元一次方程组的解? 在二元一次方程组中,适合每个方程的解。二元一次方程组的解法 一个苹果和一个梨的质量合计200g (如图1),这个苹果的质量加上10g的砝码恰好与这个梨的质量相等(如图2)。问苹果和梨的质量各多少g? x +y = 200y = x+10 你知道怎样求出它的解吗?解: 设苹果和梨的质量分别为x g 和y g。根据题意可列方程:图2图1例题讲解:你们知道曹冲称象的故事吗?你从中得到什么启示?曹冲巧妙地“以石换象”称出大象的质量现在我们模仿曹冲“以梨换苹果”再称一次梨和苹果:用x+10代替yx + (x+10) = 200( 二元 )( 一元 ) 消元 以梨换苹果答:苹果和梨的质量分别为95g和105g。 x+( x+10) = 200x = 95②怎样代入?解:①为什么可以代入?y = 105①②把②代入①得:把③代入②得:③∴原方程组的解为
解方程组的基本思路是“消元”,也是把二元一次方程组化一元一次方程。归纳小结 消元的方法是“代入”,这种解方程组的方法称为代入消元法,简称代入法。(它是解二元一次方程常用的方法之一)例1: 解方程组2y - 3x = 1
x = y - 1解:2y – 3(y – 1) = 12y – 3y + 3 = 1y = 2把③代入②,得: x = 1 得:解题思路: 通过代入消去一个未知数,把二元一次方程组转化为一元一次方程。 说明: 为了检查计算是否正确,可把所得的解分别代入方程①,②检验。 检验过程可以口算,不必写出。例题讲解:把②代入①,①②③〖分析〗解: 2x = 8+7y即 ③ 把③代入②,得 ∴ 方程组的解是 ①
② 将其中一个方程的一个未知数用另一个未知数表示时,通常我们选择的方程应使运算比较简便。 由①,得
练习提示:②用含哪个未知数的代数式表示另一个未知数?有一个未知数的系数的系数的绝对值是1。表示系数的绝对值比较小的未知数。①你认为具有什么特征的方程用代入法比较方便?1.解下列方程组用代入法解二元一次方程组的一般步骤是: ②用这个代数式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值; ③把这个未知数的值代入代数式(回代) ,求得另一个未知数的值; ①将方程组中一个方程变形,使得一个未知数能含有另一个未知数的代数式表示;④写出方程组的解。例题小结:即: 变形代替回代写出解提高巩固1.解下列二元一次方程组你认为怎样代入更简便? 请用你最简便的方法解出它的解。你的思路能解另一题吗?x+1=2(y-1)
3(x+1)=5(y-1)+4①
②⑴1.解下列二元一次方程组(分组练习)可将(x+1)、(y-1)看作一个整体求解。 解: 把①代入② 3×2(y-1)= 5(y-1) + 4 6(y-1) =5(y-1)+4 (y-1) = 4 ③ y = 5 把③代入①x +1 =8x = 7 〖分析〗得 得:①
②3x+2y=13
3x - 2y = 5⑵解下列二元一次方程组(分组练习)〖分析〗 可将2y看作一个数来求解。 解: 由②得:把③代入① 3x + (3x – 5) = 13 6x = 18 x = 3把x = 3 代入③2y = 9 – 5 y = 2 2y = 3x – 5 ③ 得: 得: 1.用代入法解方程组:2.用整体代入法解方程组:课堂小结1.消元实质2.代入法的一般步骤3.能灵活运用适当方法解二元一次方程组布置作业:A册9.5
解方程组的基本思路是“消元”,也是把二元一次方程组化一元一次方程。归纳小结 消元的方法是“代入”,这种解方程组的方法称为代入消元法,简称代入法。(它是解二元一次方程常用的方法之一)例1: 解方程组2y - 3x = 1
x = y - 1解:2y – 3(y – 1) = 12y – 3y + 3 = 1y = 2把③代入②,得: x = 1 得:解题思路: 通过代入消去一个未知数,把二元一次方程组转化为一元一次方程。 说明: 为了检查计算是否正确,可把所得的解分别代入方程①,②检验。 检验过程可以口算,不必写出。例题讲解:把②代入①,①②③〖分析〗解: 2x = 8+7y即 ③ 把③代入②,得 ∴ 方程组的解是 ①
② 将其中一个方程的一个未知数用另一个未知数表示时,通常我们选择的方程应使运算比较简便。 由①,得
练习提示:②用含哪个未知数的代数式表示另一个未知数?有一个未知数的系数的系数的绝对值是1。表示系数的绝对值比较小的未知数。①你认为具有什么特征的方程用代入法比较方便?1.解下列方程组用代入法解二元一次方程组的一般步骤是: ②用这个代数式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值; ③把这个未知数的值代入代数式(回代) ,求得另一个未知数的值; ①将方程组中一个方程变形,使得一个未知数能含有另一个未知数的代数式表示;④写出方程组的解。例题小结:即: 变形代替回代写出解提高巩固1.解下列二元一次方程组你认为怎样代入更简便? 请用你最简便的方法解出它的解。你的思路能解另一题吗?x+1=2(y-1)
3(x+1)=5(y-1)+4①
②⑴1.解下列二元一次方程组(分组练习)可将(x+1)、(y-1)看作一个整体求解。 解: 把①代入② 3×2(y-1)= 5(y-1) + 4 6(y-1) =5(y-1)+4 (y-1) = 4 ③ y = 5 把③代入①x +1 =8x = 7 〖分析〗得 得:①
②3x+2y=13
3x - 2y = 5⑵解下列二元一次方程组(分组练习)〖分析〗 可将2y看作一个数来求解。 解: 由②得:把③代入① 3x + (3x – 5) = 13 6x = 18 x = 3把x = 3 代入③2y = 9 – 5 y = 2 2y = 3x – 5 ③ 得: 得: 1.用代入法解方程组:2.用整体代入法解方程组:课堂小结1.消元实质2.代入法的一般步骤3.能灵活运用适当方法解二元一次方程组布置作业:A册9.5
