10.3.2随机模拟 课件(共11张PPT)
文档属性
| 名称 | 10.3.2随机模拟 课件(共11张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 528.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 17:04:13 | ||
图片预览




文档简介
(共11张PPT)
10.3.2 随机模拟
一、引入新课
用频率估计概率,需要做大量的重复试验,
有没有其他办法可以代替试验呢?
1.利用计算器或计算机软件
随机数和伪随机数
2.构建模拟试验
二、探究新知
一个袋中装有2个红球和3个白球,这些球除颜色不同外没有其他差别,估计从袋中摸出一个球为红球的概率.
0.39
0.416
0.385
0.44
0.45
0.4
0.35
0.6
116
104
77
66
45
20
7
6
300
250
200
150
100
50
20
10
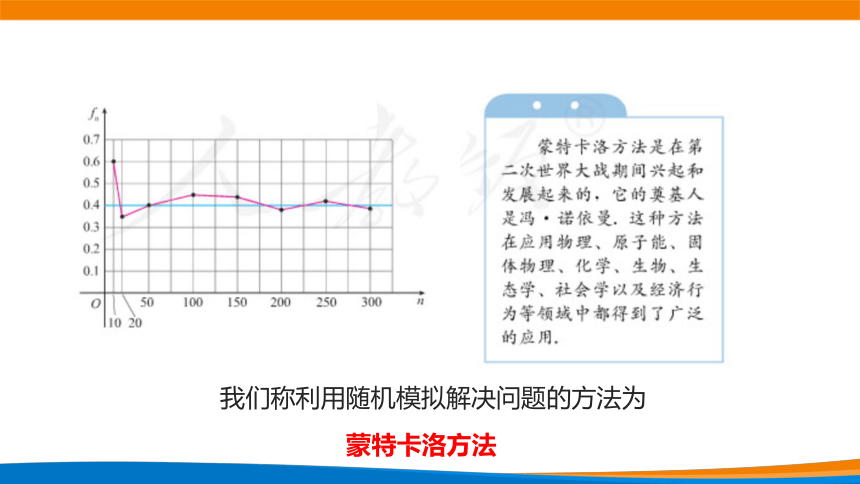
下表是用电子表格软件模拟上述摸球试验的结果,其中 为 试验次数, 为摸到红球的频数 , 为摸到红球的频率 .
我们称利用随机模拟解决问题的方法为
蒙特卡洛方法
三、巩固新知
例1.从你所在班级任意选出6名同学,调查他们出生月份,假设出生在一月,二月,··· ···十二月是等可能的.设事件A=“至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件A发生的概率.
解法1.
可以构建如下有放回的摸球试验进行模拟:在袋子中装入编号为1,2,3, ···,12的12个球,这些球除编号外没有什么差别.有放回地随机从袋中摸6次球,得到6个数代表6个人的出生月份,这就完成了一次模拟试验.如果这6个数中至少有2个相同,表示事件A发生了.重复以上模拟试验20次,就可以统计出事件A发生的频率.
解法2:
利用电子表格模拟试验.在A1,B1,C1,D1,E1,F1单元格分别输入“=RANDBETWEEN(1,12)”,得到6个数,代表6个人的出生月份,完成一次模拟试验.选中A1,B1,C1,D1,E1,F1,单元格,将鼠标指向右下角的黑点,按住鼠标左键拖动到20行,相当于做20次重复试验.统计其中有相同的频率,得到事件A的概率的估计值.
表中是20次模拟试验的结果.A发生了14次,事件A的概率的估计值为0.70.
例2.在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验,估计甲获得冠军的概率.
解:
设事件A=“甲获得冠军”, B=“单局比赛甲胜”,则P(B)=0.6.用计算机产生1~5之间的随机数,当出现随机数1,2或3时,表示一局比赛甲获胜,其概率为0.6.由于要比赛3局,所以每3个随机数为一组.例如,产生20组随机数.
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354
相当于做了20次重复试验.其中事件A发生了13次,对应的数组分别是423 123 423 114 332 152 342 512 125 432 334 151 314,用频率估计事件A的概率的近似值为
四、课堂练习
1.盒子中仅有4个白球和5个黑球,从中任意取出一个球
(1)“取出的球是黄球”是什么事件?它的概率是多少?
(2)“取出的球是白球”是什么事件?它的概率是多少?
(3)“取出的球是白球或黑球”是什么事件?它的概率是多少?
(4)设计一个用计算器或计算机模拟上面的取球试验,并模拟100次, 估计“取出的球是白球”的概率。
2.采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率.先由计算机给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347
4373 8636 6947 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
A.0.852 B.0.8192 C.0.8 D.0.75
3.若天气预报说今后的三天中每一天下雨的概率都是40%,我们可以通过随机模拟的方法估计概率.我们先产生20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
在这组数中,用0,1,2,3表示下雨,4,5,6,7,8,9表示不下雨,那么今后的三天中都下雨的概率近似为( )
课堂小结
1.随机模拟方法确定概率的估计值
2.利用随机数求简单事件的概率
作业:课本P257 练习(1)(3)
10.3.2 随机模拟
一、引入新课
用频率估计概率,需要做大量的重复试验,
有没有其他办法可以代替试验呢?
1.利用计算器或计算机软件
随机数和伪随机数
2.构建模拟试验
二、探究新知
一个袋中装有2个红球和3个白球,这些球除颜色不同外没有其他差别,估计从袋中摸出一个球为红球的概率.
0.39
0.416
0.385
0.44
0.45
0.4
0.35
0.6
116
104
77
66
45
20
7
6
300
250
200
150
100
50
20
10
下表是用电子表格软件模拟上述摸球试验的结果,其中 为 试验次数, 为摸到红球的频数 , 为摸到红球的频率 .
我们称利用随机模拟解决问题的方法为
蒙特卡洛方法
三、巩固新知
例1.从你所在班级任意选出6名同学,调查他们出生月份,假设出生在一月,二月,··· ···十二月是等可能的.设事件A=“至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件A发生的概率.
解法1.
可以构建如下有放回的摸球试验进行模拟:在袋子中装入编号为1,2,3, ···,12的12个球,这些球除编号外没有什么差别.有放回地随机从袋中摸6次球,得到6个数代表6个人的出生月份,这就完成了一次模拟试验.如果这6个数中至少有2个相同,表示事件A发生了.重复以上模拟试验20次,就可以统计出事件A发生的频率.
解法2:
利用电子表格模拟试验.在A1,B1,C1,D1,E1,F1单元格分别输入“=RANDBETWEEN(1,12)”,得到6个数,代表6个人的出生月份,完成一次模拟试验.选中A1,B1,C1,D1,E1,F1,单元格,将鼠标指向右下角的黑点,按住鼠标左键拖动到20行,相当于做20次重复试验.统计其中有相同的频率,得到事件A的概率的估计值.
表中是20次模拟试验的结果.A发生了14次,事件A的概率的估计值为0.70.
例2.在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验,估计甲获得冠军的概率.
解:
设事件A=“甲获得冠军”, B=“单局比赛甲胜”,则P(B)=0.6.用计算机产生1~5之间的随机数,当出现随机数1,2或3时,表示一局比赛甲获胜,其概率为0.6.由于要比赛3局,所以每3个随机数为一组.例如,产生20组随机数.
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354
相当于做了20次重复试验.其中事件A发生了13次,对应的数组分别是423 123 423 114 332 152 342 512 125 432 334 151 314,用频率估计事件A的概率的近似值为
四、课堂练习
1.盒子中仅有4个白球和5个黑球,从中任意取出一个球
(1)“取出的球是黄球”是什么事件?它的概率是多少?
(2)“取出的球是白球”是什么事件?它的概率是多少?
(3)“取出的球是白球或黑球”是什么事件?它的概率是多少?
(4)设计一个用计算器或计算机模拟上面的取球试验,并模拟100次, 估计“取出的球是白球”的概率。
2.采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率.先由计算机给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347
4373 8636 6947 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
A.0.852 B.0.8192 C.0.8 D.0.75
3.若天气预报说今后的三天中每一天下雨的概率都是40%,我们可以通过随机模拟的方法估计概率.我们先产生20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
在这组数中,用0,1,2,3表示下雨,4,5,6,7,8,9表示不下雨,那么今后的三天中都下雨的概率近似为( )
课堂小结
1.随机模拟方法确定概率的估计值
2.利用随机数求简单事件的概率
作业:课本P257 练习(1)(3)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
