2022-2023学年人教A版高二文科数学下学期期中达标测评卷(A卷)(含解析)
文档属性
| 名称 | 2022-2023学年人教A版高二文科数学下学期期中达标测评卷(A卷)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 617.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 10:30:34 | ||
图片预览



文档简介
2022-2023学年人教A版高二文科数学下学期期中达标测评卷(A卷)
【满分:150 分】
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设备的经济寿命是指设备从投入使用开始到因继续使用在经济上不合理而被更新所经历的时间,由维护费用的提高和使用价值的降低决定的.设备的经济寿命有如下计算公式:,其中为设备的经济寿命(单位:年),P为设备目前实际价值,为设备N年末的净残值,为设备的低劣化值.若有一台设备,目前实际价值为8000元,预计经济寿命为7年,设备的低劣化值为300元,则该设备7年末的净残值为( )
A.600元 B.650元 C.700元 D.750元
2.某品牌公司在海外设立了多个分支机构,现需要国内公司外派大量中、青年员工该企业为了解这两个年龄层的员工是否愿意被外派,采用分层抽样的方法从中、青年员工中随机抽取了100位进行调查,得到数据如下表:
愿意被外派 不愿意被外派 总计
中年员工 20 30 50
青年员工 40 10 50
总计 60 40 100
得到的正确结论是( )
A.有90%的把握认为“是否愿意被外派与年龄有关”
B.有90%的把握认为“是否愿意被外派与年龄无关”
C.有99%的把握认为“是否愿意被外派与年龄有关”
D.有99%的把握认为“是否愿意被外派与年龄无关”
3.假设有两个变量X与Y,它们的取值分别为和,其2×2列联表为
合计
a b
c d
合计
对同一样本,以下数据能说明X与Y有关的可能性最大的一组为( )
A. B.
C. D.
4.在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀,统计成绩后,得到如下列联表:
优秀 非优秀 合计
甲班 10 50 60
乙班 20 30 50
合计 30 80 110
附:,其中.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
根据独立性检验,可以认为数学考试成绩与班级有关系的把握为( )
A.95% B.99.5% C.99.9% D.99%
5.哥隆尺是一种特殊的尺子.图1的哥隆尺可以一次性度量的长度为1,2,3,4,5,6.图2的哥隆尺不能一次性度量的长度为( )
A.11 B.13 C.15 D.17
6.下列推理过程是类比推理的为( )
A.科学家通过研究蝙蝠的声波发明了雷达
B.人们通过实验得出投骰子出现数字1的概率为
C.数列,推理出
D.教室的几把椅子坏了,那么该教室内所有的椅子都坏了
7.甲、乙、丙三人从红、黄、蓝三种颜色的帽子中各选一顶戴在头上,每个人帽子的颜色互不相同.乙比戴蓝帽的人年龄大,丙和戴红帽的人年龄不同,戴红帽的人比甲年龄小,则甲、乙、丙所戴帽子的颜色分别为( )
A.红、黄、蓝 B.黄、红、蓝 C.蓝、红、黄 D.蓝、黄、红
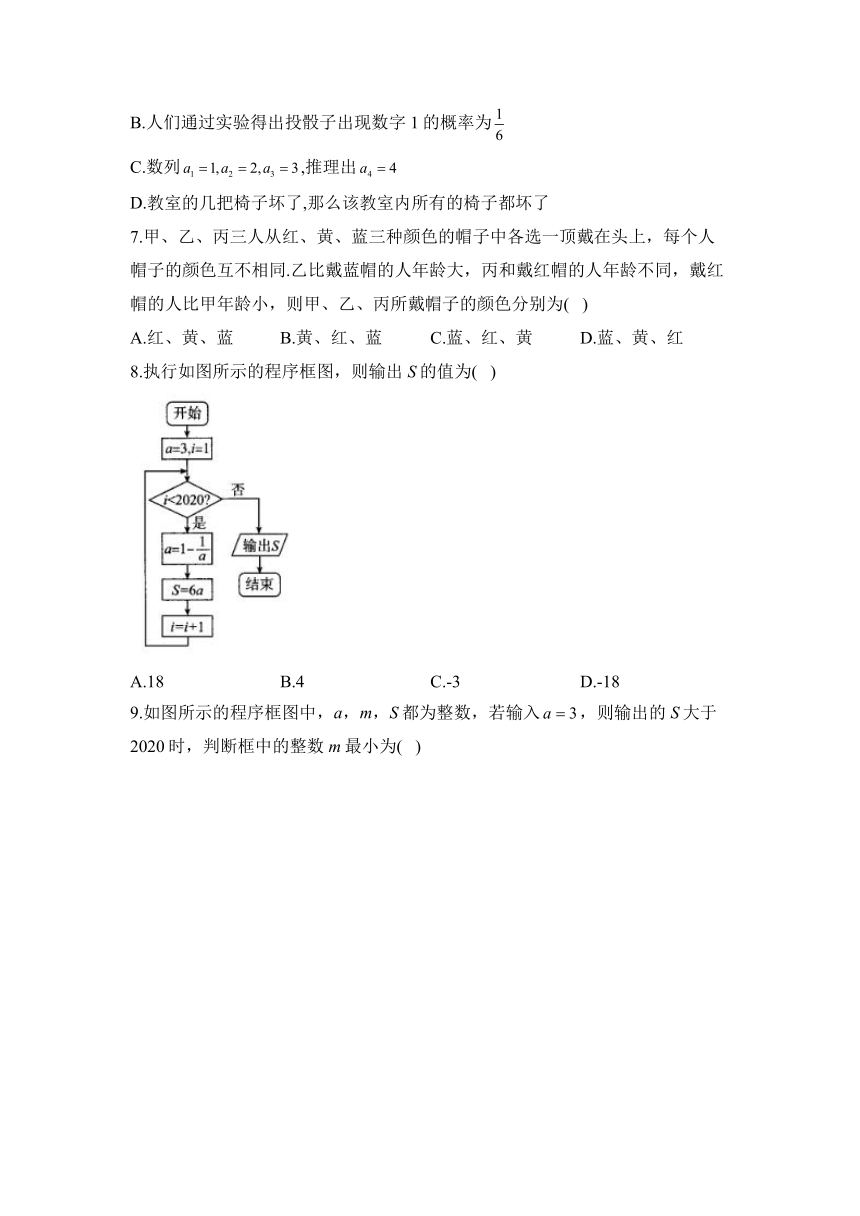
8.执行如图所示的程序框图,则输出S的值为( )
A.18 B.4 C.-3 D.-18
9.如图所示的程序框图中,a,m,S都为整数,若输入,则输出的S大于2020时,判断框中的整数m最小为( )
A.5 B.6 C.7 D.8
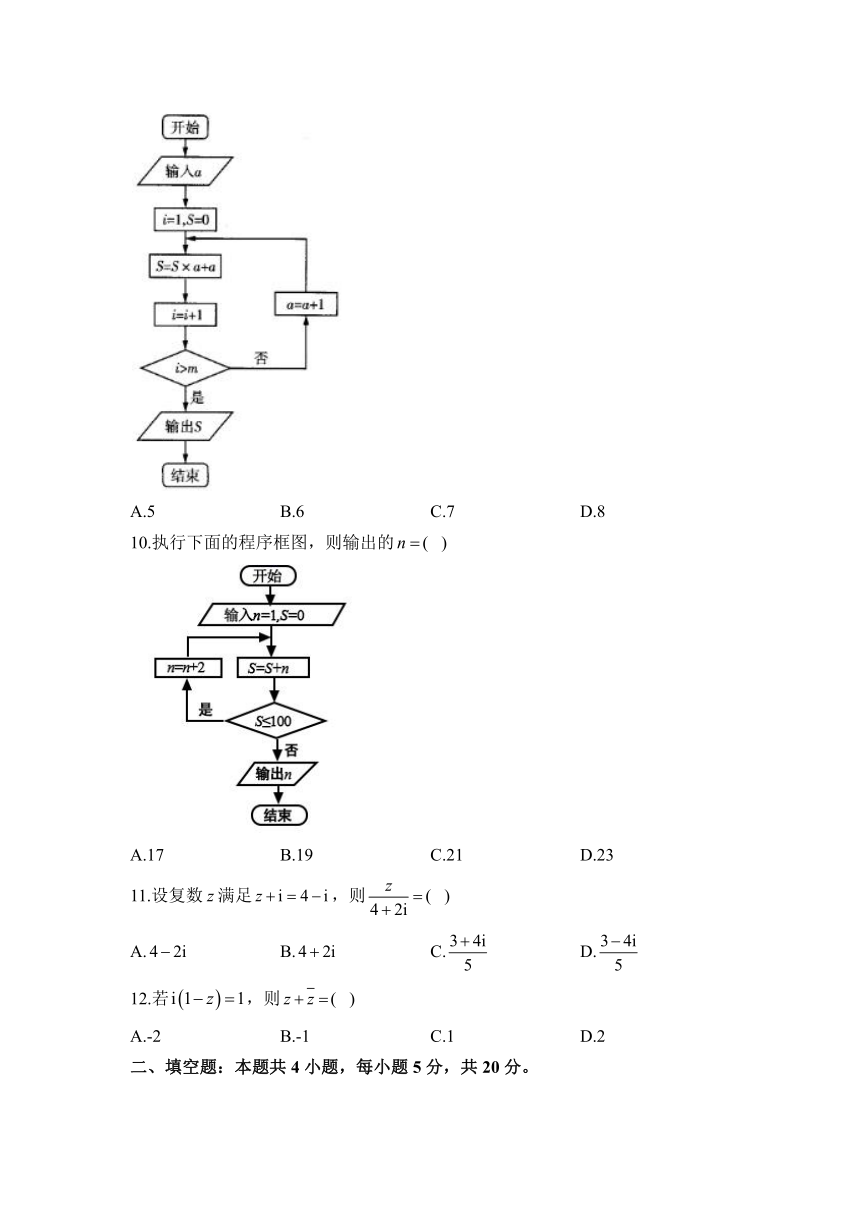
10.执行下面的程序框图,则输出的( )
A.17 B.19 C.21 D.23
11.设复数z满足,则( )
A. B. C. D.
12.若,则( )
A.-2 B.-1 C.1 D.2
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13.若复数z满足(i为虚数单位),则______.
14.执行下面的程序框图,若输出的m的值为,则输入a的值为__________.
15.甲、乙、丙三位同学获得某项竞赛活动的前三名,但具体名次未知.3人作出如下预测:甲说:我不是第三名;乙说:我是第三名;丙说:我不是第一名.若甲、乙、丙3人的预测结果有且只有一个正确,由此判断获得第三名的是__________.
16.在一次独立试验中,有200人按性别和是否色弱分类如下表所示(单位:人).
男 女
正常 73 117
色弱 7 3
你能在犯错误的概率不超过___________的前提下认为“是否色弱与性别有关”.
附:
0.10 0.05 0.01
k 2.706 3.841 6.635
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17. (10分)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 不满意
男顾客 40 10
女顾客 30 20
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异
附:.
0.050 0.010 0.001
3.841 6.635 10.828
18. (12分)设数列的前n项和为,并且满足,.
(1)猜想的通项公式,并用数学归纳法加以证明;
(2)设,,且,证明:.
19. (12分)求实数m的值,使得复数分别是:
(1)实数;
(2)纯虚数.
20. (12分)设复数,其中,当a取何值时,
(1);
(2)z是纯虚数;
(3)z是零.
21. (12分)下面图形都是由小正三角形构成的,设第n个图形中的黑点总数为.
(1)求的值;
(2)找出与的关系,并求出的表达式.
22. (12分)若复数,复数.
(1)求;
(2)若,求实数a的值.
答案以及解析
一、选择题
1.答案:B
解析:由题意知年,元,元.由,得该设备7年末的净残值(元),(提示:注意对公式中各个字母含义的准确理解)
故选B.
2.答案:C
解析:由题意,可得,所以有99%的把握认为“是否愿意被外派与年龄有关”,故选C.
3.答案:D
解析:对于同一样本,越小,说明X与Y之间关系越弱,而越大,说明X与Y之间关系越强.通过计算,知对于选项A,B,C,都有.对于选项D,有,显然.故选D.
4.答案:D
解析:由题表中的数据可得:,因为,所以可以认为数学考试成绩与班级有关系的把握为99%.故选D.
5.答案:C
解析:由题意图2中可得,,,但得不到15,故答案选C.
6.答案:A
解析:由类比推理的定义可知选项A是类比推理;由归纳推理的定义可知选项B,C,D均是归纳推理,故选A.
7.答案:B
解析:本题考查简单的逻辑推理.丙和戴红帽的人年龄不同,戴红帽的人比甲年龄小,故戴红帽的人为乙,即乙比甲的年龄小;又乙比戴蓝帽的人年龄大,故戴蓝帽的人是丙.综上所述,甲、乙、丙所戴帽子的颜色分别为黄、红、蓝.故选B.
8.答案:A
解析:根据题意,执行程序框图,,,满足条件,执行循环体;,,;,,;,,;,,;….可知S的值是以3为周期循环出现的,又由程序框图知,,,;,,.当时不满足条件,故退出循环,输出,故选A.
9.答案:A
解析:由框图可知,当S首次大于2020时满足题意的整数m最小.
模拟运行程序框图,输入,,,进入循环体,,,
第1次判断,不成立,,,;
第2次判断,不成立,,,;
第3次判断,不成立,,,;
第4次判断,不成立,,,;
第5次判断,成立,退出循环.所以此时,故选A.
10.答案:C
解析:由程序框图知S等于正奇数数列1,3,5,…的前k项和,其中,,当前k项和大于100时退出循环,则,当时,;当时,,退出循环.则输出的n的值为.故选C.
11.答案:D
解析:依题意,
.
故选:D.
12.答案:D
解析:因为,所以,所以,所以.故选D.
二、填空题
13.答案:
解析:由,
得,
所以,则,
所以.
故答案为:.
14.答案:
解析:程序运行如下:
第一次循环:,此时满足,执行;
第二次循环:,此时满足,执行;
第三次循环:,此时满足,执行;
第四次循环:,此时不满足.
输出结果为,由题意可得:,.
故答案为:.
15.答案:甲
解析:若甲的预测正确,乙与丙预测错误.则甲不是第三名,乙不是第三名,丙是第一名,即甲乙丙都不是第三名,矛盾,假设不成立;
若乙的预测正确,甲与丙预测错误.则甲是第三名,乙是第三名,丙是第一名,即甲乙都是第三名,矛盾,假设不成立;
若丙的预测正确,甲与乙预测错误.则甲是第三名,乙不是第三名,丙不是第一名,即乙是第一名,丙是第二名,甲是第三名,假设成立.
故答案为:甲.
16.答案:0.05
解析:由题意得2×2列联表为
男 女 合计
正常 73 117 190
色弱 7 3 10
合计 80 120 200
由列联表中的数据,得,所以在犯错误的概率不超过0.05的前提下可认为“是否色弱与性别有关”.
三、解答题
17.答案:(1) 男 0.8女0.6(2) 有95%
解析:(1)由调查数据知,男顾客中对该商场服务满意的比率为,因此男顾客对该商场服务满意的概率的估计值为0.8.
女顾客中对该商场服务满意的比率为,因此女顾客对该商场服务满意的概率的估计值为0.6.
(2).
由于,故有95%的把握认为男、女顾客对该商场服务的评价有差异.
18.答案:(1)分别令,2,3,得
.
,,,.
猜想:.证明如下:
,①
当时,.②
①-②,得,即.
(i)当时,,,.
(ii)假设当时,,那么当时,
,
.
,,,
.
即当时也成立,.
显然当时,也成立,
故对于一切,均有.
(2)要证,
只需证,
只需证.
即证,
将代入,得,
只需证,即证.
,,且,
,当且仅当时等号成立,即,故,
原不等式成立.
19.答案:(1)或
(2)
解析:(1)由题知,
复数为实数当且仅当,即或,
所以当或时,复数为实数.
(2)复数为纯虚数当且仅当,即,
唯一满足此条件的m的值是,
所以当时,复数为纯虚数.
20.答案:(1)或
(2)
(3)
解析:(1)若,则,解得:或.
(2)若z是纯虚数,则,解得:.
(3)若z是零,则,解得:.
21.答案:(1)由题意可得,,.
(2).
观察猜想: 是一个首项为9,公差为6的等差数列,即.
因为,
,
………
.
把上述式子累加可得到.
又因为,所以.而当时,也满足上式,故.
22.答案:(1)5
(2)
解析:(1)因为,所以;
(2),由可得,解得.
【满分:150 分】
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设备的经济寿命是指设备从投入使用开始到因继续使用在经济上不合理而被更新所经历的时间,由维护费用的提高和使用价值的降低决定的.设备的经济寿命有如下计算公式:,其中为设备的经济寿命(单位:年),P为设备目前实际价值,为设备N年末的净残值,为设备的低劣化值.若有一台设备,目前实际价值为8000元,预计经济寿命为7年,设备的低劣化值为300元,则该设备7年末的净残值为( )
A.600元 B.650元 C.700元 D.750元
2.某品牌公司在海外设立了多个分支机构,现需要国内公司外派大量中、青年员工该企业为了解这两个年龄层的员工是否愿意被外派,采用分层抽样的方法从中、青年员工中随机抽取了100位进行调查,得到数据如下表:
愿意被外派 不愿意被外派 总计
中年员工 20 30 50
青年员工 40 10 50
总计 60 40 100
得到的正确结论是( )
A.有90%的把握认为“是否愿意被外派与年龄有关”
B.有90%的把握认为“是否愿意被外派与年龄无关”
C.有99%的把握认为“是否愿意被外派与年龄有关”
D.有99%的把握认为“是否愿意被外派与年龄无关”
3.假设有两个变量X与Y,它们的取值分别为和,其2×2列联表为
合计
a b
c d
合计
对同一样本,以下数据能说明X与Y有关的可能性最大的一组为( )
A. B.
C. D.
4.在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀,统计成绩后,得到如下列联表:
优秀 非优秀 合计
甲班 10 50 60
乙班 20 30 50
合计 30 80 110
附:,其中.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
根据独立性检验,可以认为数学考试成绩与班级有关系的把握为( )
A.95% B.99.5% C.99.9% D.99%
5.哥隆尺是一种特殊的尺子.图1的哥隆尺可以一次性度量的长度为1,2,3,4,5,6.图2的哥隆尺不能一次性度量的长度为( )
A.11 B.13 C.15 D.17
6.下列推理过程是类比推理的为( )
A.科学家通过研究蝙蝠的声波发明了雷达
B.人们通过实验得出投骰子出现数字1的概率为
C.数列,推理出
D.教室的几把椅子坏了,那么该教室内所有的椅子都坏了
7.甲、乙、丙三人从红、黄、蓝三种颜色的帽子中各选一顶戴在头上,每个人帽子的颜色互不相同.乙比戴蓝帽的人年龄大,丙和戴红帽的人年龄不同,戴红帽的人比甲年龄小,则甲、乙、丙所戴帽子的颜色分别为( )
A.红、黄、蓝 B.黄、红、蓝 C.蓝、红、黄 D.蓝、黄、红
8.执行如图所示的程序框图,则输出S的值为( )
A.18 B.4 C.-3 D.-18
9.如图所示的程序框图中,a,m,S都为整数,若输入,则输出的S大于2020时,判断框中的整数m最小为( )
A.5 B.6 C.7 D.8
10.执行下面的程序框图,则输出的( )
A.17 B.19 C.21 D.23
11.设复数z满足,则( )
A. B. C. D.
12.若,则( )
A.-2 B.-1 C.1 D.2
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13.若复数z满足(i为虚数单位),则______.
14.执行下面的程序框图,若输出的m的值为,则输入a的值为__________.
15.甲、乙、丙三位同学获得某项竞赛活动的前三名,但具体名次未知.3人作出如下预测:甲说:我不是第三名;乙说:我是第三名;丙说:我不是第一名.若甲、乙、丙3人的预测结果有且只有一个正确,由此判断获得第三名的是__________.
16.在一次独立试验中,有200人按性别和是否色弱分类如下表所示(单位:人).
男 女
正常 73 117
色弱 7 3
你能在犯错误的概率不超过___________的前提下认为“是否色弱与性别有关”.
附:
0.10 0.05 0.01
k 2.706 3.841 6.635
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17. (10分)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 不满意
男顾客 40 10
女顾客 30 20
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异
附:.
0.050 0.010 0.001
3.841 6.635 10.828
18. (12分)设数列的前n项和为,并且满足,.
(1)猜想的通项公式,并用数学归纳法加以证明;
(2)设,,且,证明:.
19. (12分)求实数m的值,使得复数分别是:
(1)实数;
(2)纯虚数.
20. (12分)设复数,其中,当a取何值时,
(1);
(2)z是纯虚数;
(3)z是零.
21. (12分)下面图形都是由小正三角形构成的,设第n个图形中的黑点总数为.
(1)求的值;
(2)找出与的关系,并求出的表达式.
22. (12分)若复数,复数.
(1)求;
(2)若,求实数a的值.
答案以及解析
一、选择题
1.答案:B
解析:由题意知年,元,元.由,得该设备7年末的净残值(元),(提示:注意对公式中各个字母含义的准确理解)
故选B.
2.答案:C
解析:由题意,可得,所以有99%的把握认为“是否愿意被外派与年龄有关”,故选C.
3.答案:D
解析:对于同一样本,越小,说明X与Y之间关系越弱,而越大,说明X与Y之间关系越强.通过计算,知对于选项A,B,C,都有.对于选项D,有,显然.故选D.
4.答案:D
解析:由题表中的数据可得:,因为,所以可以认为数学考试成绩与班级有关系的把握为99%.故选D.
5.答案:C
解析:由题意图2中可得,,,但得不到15,故答案选C.
6.答案:A
解析:由类比推理的定义可知选项A是类比推理;由归纳推理的定义可知选项B,C,D均是归纳推理,故选A.
7.答案:B
解析:本题考查简单的逻辑推理.丙和戴红帽的人年龄不同,戴红帽的人比甲年龄小,故戴红帽的人为乙,即乙比甲的年龄小;又乙比戴蓝帽的人年龄大,故戴蓝帽的人是丙.综上所述,甲、乙、丙所戴帽子的颜色分别为黄、红、蓝.故选B.
8.答案:A
解析:根据题意,执行程序框图,,,满足条件,执行循环体;,,;,,;,,;,,;….可知S的值是以3为周期循环出现的,又由程序框图知,,,;,,.当时不满足条件,故退出循环,输出,故选A.
9.答案:A
解析:由框图可知,当S首次大于2020时满足题意的整数m最小.
模拟运行程序框图,输入,,,进入循环体,,,
第1次判断,不成立,,,;
第2次判断,不成立,,,;
第3次判断,不成立,,,;
第4次判断,不成立,,,;
第5次判断,成立,退出循环.所以此时,故选A.
10.答案:C
解析:由程序框图知S等于正奇数数列1,3,5,…的前k项和,其中,,当前k项和大于100时退出循环,则,当时,;当时,,退出循环.则输出的n的值为.故选C.
11.答案:D
解析:依题意,
.
故选:D.
12.答案:D
解析:因为,所以,所以,所以.故选D.
二、填空题
13.答案:
解析:由,
得,
所以,则,
所以.
故答案为:.
14.答案:
解析:程序运行如下:
第一次循环:,此时满足,执行;
第二次循环:,此时满足,执行;
第三次循环:,此时满足,执行;
第四次循环:,此时不满足.
输出结果为,由题意可得:,.
故答案为:.
15.答案:甲
解析:若甲的预测正确,乙与丙预测错误.则甲不是第三名,乙不是第三名,丙是第一名,即甲乙丙都不是第三名,矛盾,假设不成立;
若乙的预测正确,甲与丙预测错误.则甲是第三名,乙是第三名,丙是第一名,即甲乙都是第三名,矛盾,假设不成立;
若丙的预测正确,甲与乙预测错误.则甲是第三名,乙不是第三名,丙不是第一名,即乙是第一名,丙是第二名,甲是第三名,假设成立.
故答案为:甲.
16.答案:0.05
解析:由题意得2×2列联表为
男 女 合计
正常 73 117 190
色弱 7 3 10
合计 80 120 200
由列联表中的数据,得,所以在犯错误的概率不超过0.05的前提下可认为“是否色弱与性别有关”.
三、解答题
17.答案:(1) 男 0.8女0.6(2) 有95%
解析:(1)由调查数据知,男顾客中对该商场服务满意的比率为,因此男顾客对该商场服务满意的概率的估计值为0.8.
女顾客中对该商场服务满意的比率为,因此女顾客对该商场服务满意的概率的估计值为0.6.
(2).
由于,故有95%的把握认为男、女顾客对该商场服务的评价有差异.
18.答案:(1)分别令,2,3,得
.
,,,.
猜想:.证明如下:
,①
当时,.②
①-②,得,即.
(i)当时,,,.
(ii)假设当时,,那么当时,
,
.
,,,
.
即当时也成立,.
显然当时,也成立,
故对于一切,均有.
(2)要证,
只需证,
只需证.
即证,
将代入,得,
只需证,即证.
,,且,
,当且仅当时等号成立,即,故,
原不等式成立.
19.答案:(1)或
(2)
解析:(1)由题知,
复数为实数当且仅当,即或,
所以当或时,复数为实数.
(2)复数为纯虚数当且仅当,即,
唯一满足此条件的m的值是,
所以当时,复数为纯虚数.
20.答案:(1)或
(2)
(3)
解析:(1)若,则,解得:或.
(2)若z是纯虚数,则,解得:.
(3)若z是零,则,解得:.
21.答案:(1)由题意可得,,.
(2).
观察猜想: 是一个首项为9,公差为6的等差数列,即.
因为,
,
………
.
把上述式子累加可得到.
又因为,所以.而当时,也满足上式,故.
22.答案:(1)5
(2)
解析:(1)因为,所以;
(2),由可得,解得.
同课章节目录
