2022-2023学年人教A版高二文科数学下学期期中达标测评卷(B卷)(含解析)
文档属性
| 名称 | 2022-2023学年人教A版高二文科数学下学期期中达标测评卷(B卷)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 575.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 10:32:03 | ||
图片预览



文档简介
2022-2023学年人教A版高二文科数学下学期期中达标测评卷(B卷)
【满分:150 分】
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某化工厂产生的废气经过过滤后排放,以模型去拟合过滤过程中废气的污染物浓度Ymg/L与时间Xh之间的一组数据,为了求出线性回归方程,设,其变换后得到线性回归方程为,则当经过6h后,预报废气的污染物浓度为( )
A. B. C. D.
2.变量X与Y相对应的一组数据为;变量U与V相对应的一组数据为,表示变量Y与X之间的线性相关系数,表示变量V与U之间的线性相关系数,则( )
A. B. C. D.
3.第24届冬季奥林匹克运动会将于2022年在北京举办.为了解某城市居民对冰雪运动的关注情况,随机抽取了该市100人进行调查统计,得到如下列联表.
男 女 合计
关注冰雪运动 35 25 60
不关注冰雪运动 15 25 40
合计 50 50 100
参考公式:,其中.
附表:
0.100 0.050 0.010 0.001
2.706 3.841 6.635 10.828
根据列联表可知( )
A.该市女性居民中大约有的人关注冰雪运动
B.该市男性届民中大约有的人关注冰雪运动
C.有的把握认为该市居民是否关注冰雪运动与性别有关
D.有的把握认为该市居民是否关注冰雪运动与性别有关
4.用数学归纳法证明“能被9整除”,在假设时命题成立之后,需证明时命题也成立,这时除了用归纳假设外,还需证明能被9整除的余项是( )
A. B. C. D.
5.学校艺术节对同一类的A,B,C,D四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
甲说:“A作品获得一等奖”;
乙说:“C作品获得一等奖”;
丙说:“B,D两项作品未获得一等奖”;
丁说:“A或D作品获得一等奖”.
评奖揭晓后发现这四位同学中只有两位预测正确,则获得一等奖的作品是( )
A.A作品 B.B作品 C.C作品 D.D作品
6.用数学归纳法证明命题“当n为奇数时,能被整除”,在证明正确后,归纳假设应写成( )
A.假设时命题成立 B.假设时命题成立
C.假设时命题成立 D.假设时命题成立
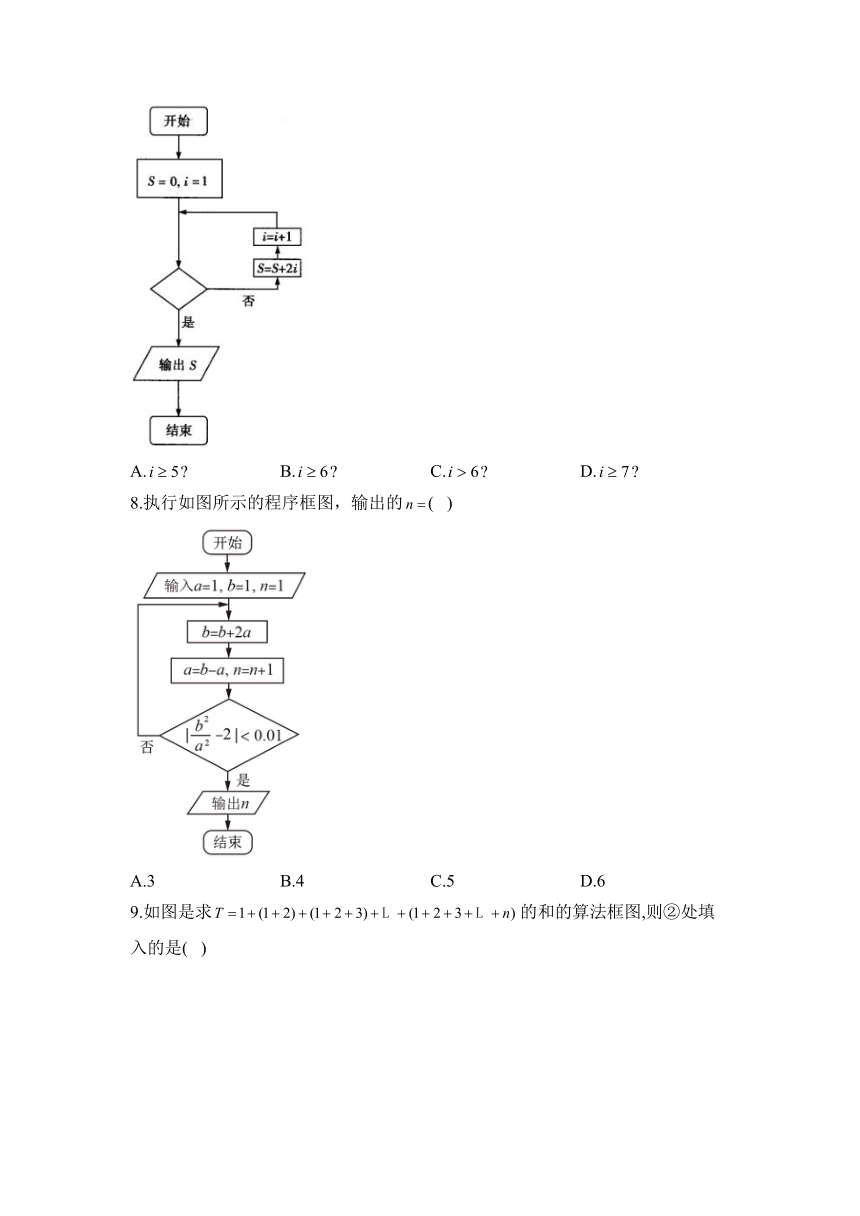
7.执行如图所示的程序框图,若输出的,则判断框中可填( )
A. B. C. D.
8.执行如图所示的程序框图,输出的( )
A.3 B.4 C.5 D.6
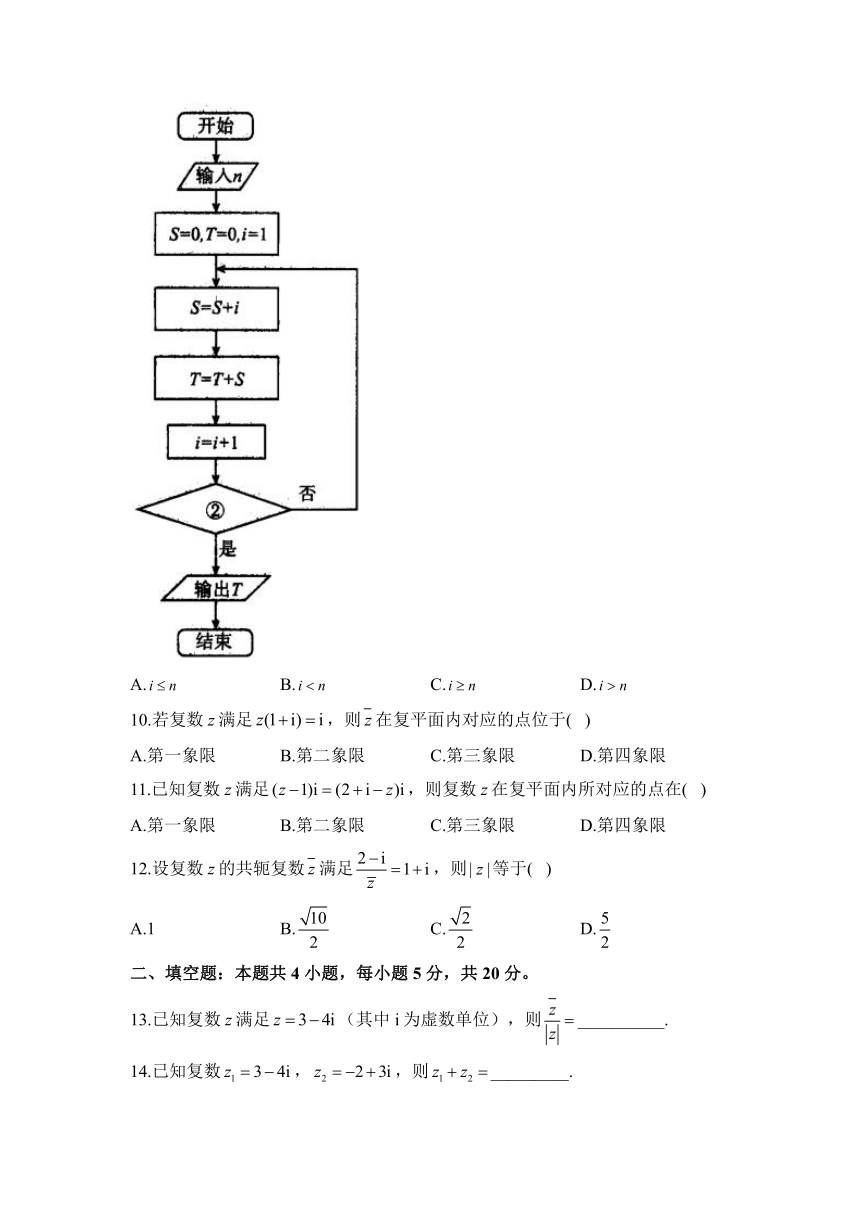
9.如图是求的和的算法框图,则②处填入的是( )
A. B. C. D.
10.若复数z满足,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.已知复数z满足,则复数z在复平面内所对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.设复数z的共轭复数满足,则等于( )
A.1 B. C. D.
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13.已知复数z满足(其中i为虚数单位),则__________.
14.已知复数,,则_________.
15.执行下边的程序框图,若输入的的值分别为0和9,则输出的i的值为__________.
16.在独立性检验中,统计量有两个临界值:3.841和6.635.当时,至少有的把握说明两个事件有关,当时,至少有的把握说明两个事件有关,当时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了200人,经计算.根据这一数据分析,我们可认为打鼾与患心脏病之间是___________的(填“有关”或“无关”).
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17. (10分)2021年5月22日10时40分,“祝融号”火星车已安全驶离着陆平台,到达火星表面,开始巡视探测.为了增强学生的科技意识,某学校进行了一次专题讲座,讲座结束后,进行了一次专题测试(满分:100分),其中理科学生有600名学生参与测试,其得分都在内,得分情况绘制成频率分布直方图如下,在区间的频率依次构成等差数列.
若规定得分不低于80分者为优秀,文科生有400名学生参与测试,其中得分优秀的学生有50名.
(1)若以每组数据的中间值代替本组数据,求理科学生得分的平均值;
(2)请根据所给数据完成下面的列联表,并说明是否有99.9%以上的把握认为,得分是否优秀与文理科有关?
优秀 不优秀 合计
理科生
文科生
合计 1000
附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
18. (12分)已知数列的各项均为正整数,对于任意,都有成立,且.
(1)求,的值;
(2)猜想数列的通项公式,并给出证明.
19. (12分)数列的前n项和为,且.
(1)求的值;
(2)猜想的表达式,并用数学归纳法加以证明.
20. (12分)已知复数,且,求实数a的取值范围.
21. (12分)设复数,试求m取何值时?
(1)z是实数.
(2)z对应的点位于复平面的第一象限.
22. (12分)实数k分别为何值时,复数满足下列条件?
(1)是实数.
(2)是虚数.
(3)是纯虚数.
(4)是0.
答案以及解析
一、选择题
1.答案:D
解析:当时,,所以.
2.答案:C
解析:由变量X与Y相对应的一组数据为,可得变量Y与X正相关,所以.
而由变量U与V相对应的一组数据为,可知变量V与U负相关,所以.因此与的大小关系是.
3.答案:C
解析:由列联表中的数据可得,因此,有的把握认为该市居民是否关注冰雪运动与性别有关.故选:C.
4.答案:A
解析:假设当时命题成立,即能被9整除,当时,.因为能被9整除,所以要证上式能被9整除,还需证明也能被9整除.
5.答案:C
解析:若获得一等奖的作品是A,则甲、丙、丁预测正确,与已知矛盾,A不正确;
若获得一等奖的作品是B,则甲、乙、丙、丁预测都不正确,与已知矛盾,B不正确;
若获得一等奖的作品是C,则只有乙、丙预测正确,与已知相符,C正确;
若获得一等奖的作品是D,则只有丁预测正确,与已知矛盾,D不正确.
故选C.
6.答案:D
解析:此题所成立的数是所有的正奇数,根据数学归纳法的证题步骤要求,第二步所取的值的范围应从开始取值所有奇数,即.
7.答案:B
解析:模拟执行程序框图,,此时条件不成立,得到,;此时条件不成立,得到,;此时条件不成立,得到,;此时条件不成立,得到,;此时条件不成立,得到,;此时条件成立,输出.结合选项可知判断框中可填“”,故选B.
8.答案:B
解析:执行循环体,,,,;,,,;,,,.故输出的,故选B.
9.答案:D
解析:根据题意,S表示的和,该循环结构为直到型循环结构,直到条件满足结束循环,故②处填,故选D.
10.答案:D
解析:由题意可得,复数,所以,其在复平面内对应的点的坐标为,即在复平面内对应的点位于第四象限,故选D.
11.答案:A
解析:由得,则,
因此复数z在复平面内所对应的点为,位于第一象限,故选A.
12.答案:B
解析:,,.故选B.
二、填空题
13.答案:
解析:由题意可得,,.
所以,.
故答案为:.
14.答案:
解析:因为,,
所以.
故答案为:.
15.答案:3
解析:第一次循环: ,;第二次循环:,;第三次循环:,;满足条件,结束循环,此时,.
16.答案:有关
解析:时,至少有的把握认为打鼾与患心脏病有关.
三、解答题
17.答案:(1)理科学生得分的平均值为73分.
(2)表格见解析,有99.9%以上的把握认为得分是否优秀与文理科有关.
解析:(1)由第三、二、四组的频率依次构成等差数列可得.
又频率分布直方图中所有小矩形面积之和为1,则,
解得,
理科学生得分的平均值为(分).
(2)理科学生优秀的人数为,
补全2×2列联表如表所示,
优秀 不优秀 合计
理科生 150 450 600
文科生 50 350 400
合计 200 800 1000
,
有99.9%以上的把握认为得分是否优秀与文理科有关.
18.答案:(1)因为,,
所以当时,,
即,
解得.
因为为正整数,所以.
当时,由,
即,
解得,
因为为正整数,所以.
(2)由,,,猜想.
下面用数学归纳法证明.
①当,2,3时,由(1)知均成立.
②假设当时猜想成立,则,
那么,
所以,
所以.
因为,,,
又,所以,
即当时,也成立.
由①②知,对任意,猜想均成立.
19.答案:(1)当时,,
当时,,
当时,,
所以.
(2)由(1)可知,
猜想:,
用数学归纳法证明如下:
①当时,,猜想成立;
②假设当时,猜想成立,即,
当时, ,
所以,
所以当时,猜想也成立.
由①②可知,对任意的都成立.
20.答案:
解析:方法一:因为,
所以,
由已知得,
所以,所以.
方法二:由知z在复平面内对应的点在以原点为圆心,以4为半径的圆内(不包括边界),由知z对应的点在直线上,
所以线段AB(除去端点)为动点的集合,由图可知.
21.答案:(1)或
(2)或
解析:(1)由且,
解得或,复数表示实数.
(2)由,且,
解得或,
故当或时,
复数z对应的点位于复平面的第一象限.
22.答案:(1)或.
(2)且.
(3).
(4).
解析:(1)
.
当,即或时,该复数为实数.
(2)当,即且时,该复数为虚数.
(3)当即时,该复数为纯虚数.
(4)当即时,该复数为0.
【满分:150 分】
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某化工厂产生的废气经过过滤后排放,以模型去拟合过滤过程中废气的污染物浓度Ymg/L与时间Xh之间的一组数据,为了求出线性回归方程,设,其变换后得到线性回归方程为,则当经过6h后,预报废气的污染物浓度为( )
A. B. C. D.
2.变量X与Y相对应的一组数据为;变量U与V相对应的一组数据为,表示变量Y与X之间的线性相关系数,表示变量V与U之间的线性相关系数,则( )
A. B. C. D.
3.第24届冬季奥林匹克运动会将于2022年在北京举办.为了解某城市居民对冰雪运动的关注情况,随机抽取了该市100人进行调查统计,得到如下列联表.
男 女 合计
关注冰雪运动 35 25 60
不关注冰雪运动 15 25 40
合计 50 50 100
参考公式:,其中.
附表:
0.100 0.050 0.010 0.001
2.706 3.841 6.635 10.828
根据列联表可知( )
A.该市女性居民中大约有的人关注冰雪运动
B.该市男性届民中大约有的人关注冰雪运动
C.有的把握认为该市居民是否关注冰雪运动与性别有关
D.有的把握认为该市居民是否关注冰雪运动与性别有关
4.用数学归纳法证明“能被9整除”,在假设时命题成立之后,需证明时命题也成立,这时除了用归纳假设外,还需证明能被9整除的余项是( )
A. B. C. D.
5.学校艺术节对同一类的A,B,C,D四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
甲说:“A作品获得一等奖”;
乙说:“C作品获得一等奖”;
丙说:“B,D两项作品未获得一等奖”;
丁说:“A或D作品获得一等奖”.
评奖揭晓后发现这四位同学中只有两位预测正确,则获得一等奖的作品是( )
A.A作品 B.B作品 C.C作品 D.D作品
6.用数学归纳法证明命题“当n为奇数时,能被整除”,在证明正确后,归纳假设应写成( )
A.假设时命题成立 B.假设时命题成立
C.假设时命题成立 D.假设时命题成立
7.执行如图所示的程序框图,若输出的,则判断框中可填( )
A. B. C. D.
8.执行如图所示的程序框图,输出的( )
A.3 B.4 C.5 D.6
9.如图是求的和的算法框图,则②处填入的是( )
A. B. C. D.
10.若复数z满足,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.已知复数z满足,则复数z在复平面内所对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.设复数z的共轭复数满足,则等于( )
A.1 B. C. D.
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13.已知复数z满足(其中i为虚数单位),则__________.
14.已知复数,,则_________.
15.执行下边的程序框图,若输入的的值分别为0和9,则输出的i的值为__________.
16.在独立性检验中,统计量有两个临界值:3.841和6.635.当时,至少有的把握说明两个事件有关,当时,至少有的把握说明两个事件有关,当时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了200人,经计算.根据这一数据分析,我们可认为打鼾与患心脏病之间是___________的(填“有关”或“无关”).
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17. (10分)2021年5月22日10时40分,“祝融号”火星车已安全驶离着陆平台,到达火星表面,开始巡视探测.为了增强学生的科技意识,某学校进行了一次专题讲座,讲座结束后,进行了一次专题测试(满分:100分),其中理科学生有600名学生参与测试,其得分都在内,得分情况绘制成频率分布直方图如下,在区间的频率依次构成等差数列.
若规定得分不低于80分者为优秀,文科生有400名学生参与测试,其中得分优秀的学生有50名.
(1)若以每组数据的中间值代替本组数据,求理科学生得分的平均值;
(2)请根据所给数据完成下面的列联表,并说明是否有99.9%以上的把握认为,得分是否优秀与文理科有关?
优秀 不优秀 合计
理科生
文科生
合计 1000
附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
18. (12分)已知数列的各项均为正整数,对于任意,都有成立,且.
(1)求,的值;
(2)猜想数列的通项公式,并给出证明.
19. (12分)数列的前n项和为,且.
(1)求的值;
(2)猜想的表达式,并用数学归纳法加以证明.
20. (12分)已知复数,且,求实数a的取值范围.
21. (12分)设复数,试求m取何值时?
(1)z是实数.
(2)z对应的点位于复平面的第一象限.
22. (12分)实数k分别为何值时,复数满足下列条件?
(1)是实数.
(2)是虚数.
(3)是纯虚数.
(4)是0.
答案以及解析
一、选择题
1.答案:D
解析:当时,,所以.
2.答案:C
解析:由变量X与Y相对应的一组数据为,可得变量Y与X正相关,所以.
而由变量U与V相对应的一组数据为,可知变量V与U负相关,所以.因此与的大小关系是.
3.答案:C
解析:由列联表中的数据可得,因此,有的把握认为该市居民是否关注冰雪运动与性别有关.故选:C.
4.答案:A
解析:假设当时命题成立,即能被9整除,当时,.因为能被9整除,所以要证上式能被9整除,还需证明也能被9整除.
5.答案:C
解析:若获得一等奖的作品是A,则甲、丙、丁预测正确,与已知矛盾,A不正确;
若获得一等奖的作品是B,则甲、乙、丙、丁预测都不正确,与已知矛盾,B不正确;
若获得一等奖的作品是C,则只有乙、丙预测正确,与已知相符,C正确;
若获得一等奖的作品是D,则只有丁预测正确,与已知矛盾,D不正确.
故选C.
6.答案:D
解析:此题所成立的数是所有的正奇数,根据数学归纳法的证题步骤要求,第二步所取的值的范围应从开始取值所有奇数,即.
7.答案:B
解析:模拟执行程序框图,,此时条件不成立,得到,;此时条件不成立,得到,;此时条件不成立,得到,;此时条件不成立,得到,;此时条件不成立,得到,;此时条件成立,输出.结合选项可知判断框中可填“”,故选B.
8.答案:B
解析:执行循环体,,,,;,,,;,,,.故输出的,故选B.
9.答案:D
解析:根据题意,S表示的和,该循环结构为直到型循环结构,直到条件满足结束循环,故②处填,故选D.
10.答案:D
解析:由题意可得,复数,所以,其在复平面内对应的点的坐标为,即在复平面内对应的点位于第四象限,故选D.
11.答案:A
解析:由得,则,
因此复数z在复平面内所对应的点为,位于第一象限,故选A.
12.答案:B
解析:,,.故选B.
二、填空题
13.答案:
解析:由题意可得,,.
所以,.
故答案为:.
14.答案:
解析:因为,,
所以.
故答案为:.
15.答案:3
解析:第一次循环: ,;第二次循环:,;第三次循环:,;满足条件,结束循环,此时,.
16.答案:有关
解析:时,至少有的把握认为打鼾与患心脏病有关.
三、解答题
17.答案:(1)理科学生得分的平均值为73分.
(2)表格见解析,有99.9%以上的把握认为得分是否优秀与文理科有关.
解析:(1)由第三、二、四组的频率依次构成等差数列可得.
又频率分布直方图中所有小矩形面积之和为1,则,
解得,
理科学生得分的平均值为(分).
(2)理科学生优秀的人数为,
补全2×2列联表如表所示,
优秀 不优秀 合计
理科生 150 450 600
文科生 50 350 400
合计 200 800 1000
,
有99.9%以上的把握认为得分是否优秀与文理科有关.
18.答案:(1)因为,,
所以当时,,
即,
解得.
因为为正整数,所以.
当时,由,
即,
解得,
因为为正整数,所以.
(2)由,,,猜想.
下面用数学归纳法证明.
①当,2,3时,由(1)知均成立.
②假设当时猜想成立,则,
那么,
所以,
所以.
因为,,,
又,所以,
即当时,也成立.
由①②知,对任意,猜想均成立.
19.答案:(1)当时,,
当时,,
当时,,
所以.
(2)由(1)可知,
猜想:,
用数学归纳法证明如下:
①当时,,猜想成立;
②假设当时,猜想成立,即,
当时, ,
所以,
所以当时,猜想也成立.
由①②可知,对任意的都成立.
20.答案:
解析:方法一:因为,
所以,
由已知得,
所以,所以.
方法二:由知z在复平面内对应的点在以原点为圆心,以4为半径的圆内(不包括边界),由知z对应的点在直线上,
所以线段AB(除去端点)为动点的集合,由图可知.
21.答案:(1)或
(2)或
解析:(1)由且,
解得或,复数表示实数.
(2)由,且,
解得或,
故当或时,
复数z对应的点位于复平面的第一象限.
22.答案:(1)或.
(2)且.
(3).
(4).
解析:(1)
.
当,即或时,该复数为实数.
(2)当,即且时,该复数为虚数.
(3)当即时,该复数为纯虚数.
(4)当即时,该复数为0.
同课章节目录
