不等式的概念和性质[上学期]
图片预览






文档简介
课件37张PPT。(1)什么是等式?
等式中“=”两侧的代数式能否交换?创设情境,复习导入 (1) 什么是等式?
回顾表示相等关系的式子。(2) 等式中“=”两侧的
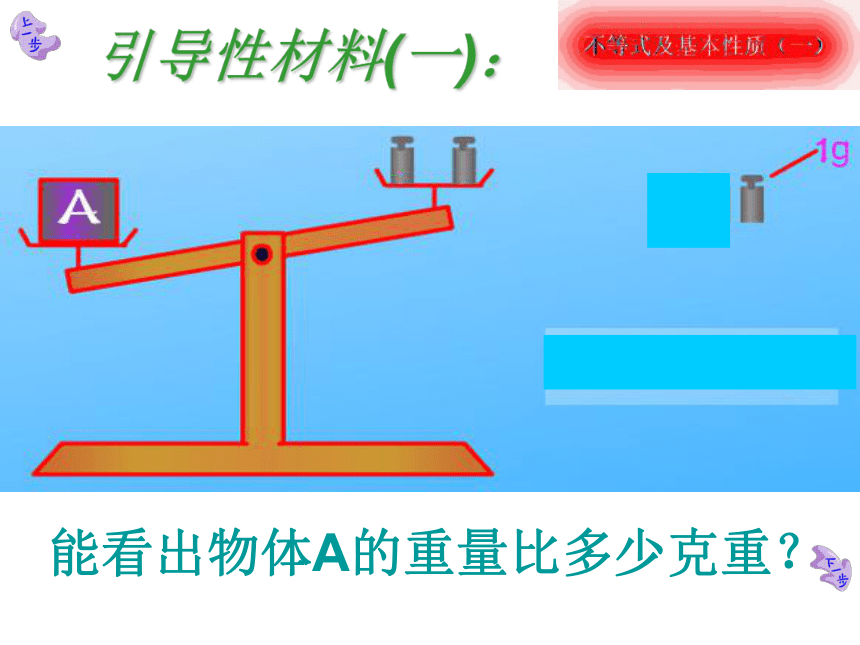
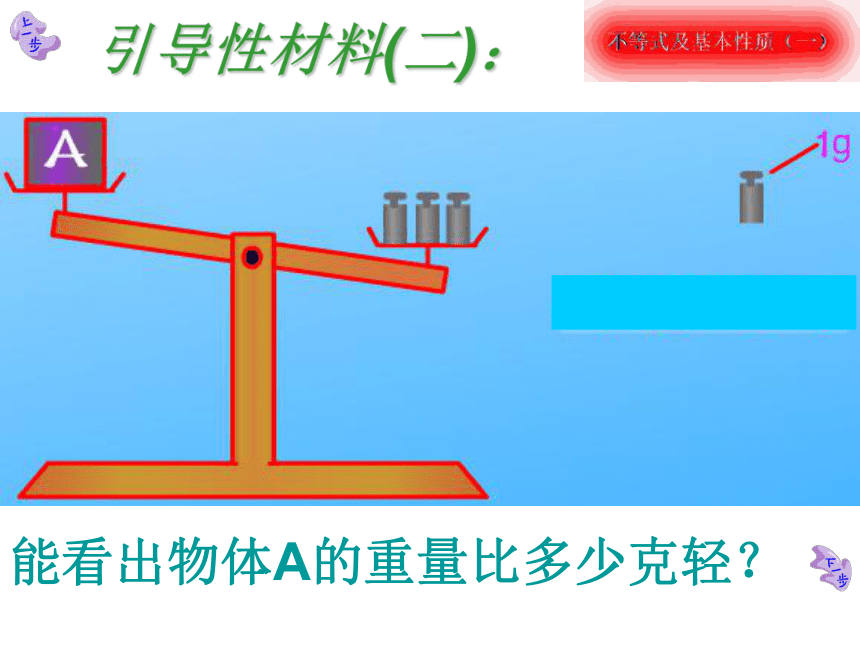
代数式能否交换?能看出物体A的重量比多少克重?引导性材料(一):引导性材料(二):能看出物体A的重量比多少克轻?据气象预报,某天的最高气温是10℃,最低气温
为-5℃,由此我们说这一天的气温不低于 ℃,
并且不高于 ℃;-510引导性材料(三):不等式及
不等式的性质如:t≥-5, t≤10“≥” 是指“>”与“=”结合起来,读作“大于或 等于”,也可理解成“不小于”“≤” 是指“<”与“=”结合起来,读作“小于或 等于”,也可理解成“不大于” 用不等号(“<” “>” “≠” “≥”“≤” )表示不等关系的式子叫不等式.
不等式定义:“<” “>” “≠” “≥” “≤”认识 x>2, x <3, a <17
-7<-5, 3+4>1+4, 5+3≠12-5
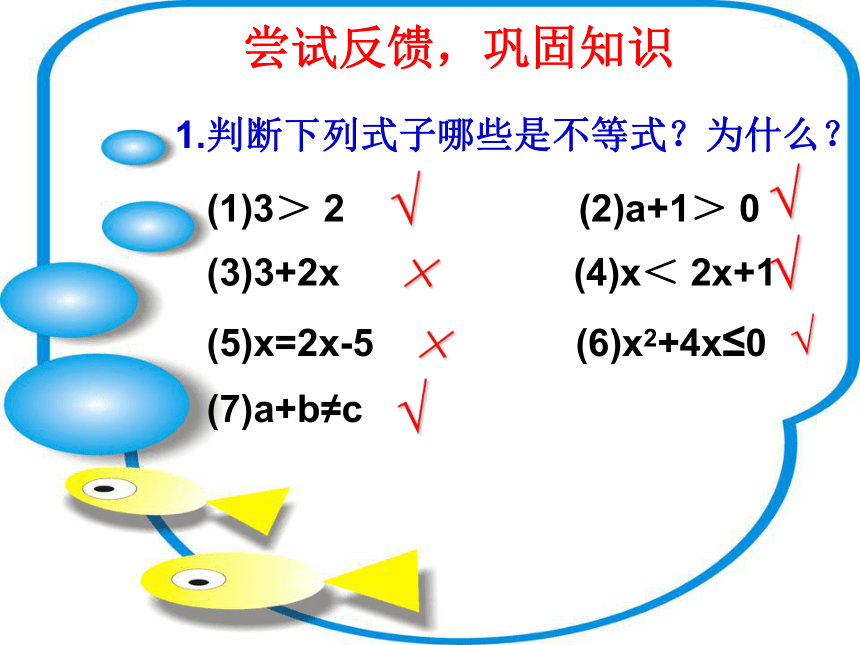
a+2>a+1, x+3 <6 , a≠0,(l)上述式子中有哪些表示数量关系的符号?(2)这些符号表示什么关系?(3)这些符号两侧的代数式可以随意交换位置吗?(“<” “>” “≠” )(左右两边不相等)(除了“≠”,其余符号都不可以)1.判断下列式子哪些是不等式?为什么?
(1)3> 2 (2)a+1> 0 (3)3+2x (4)x< 2x+1 (5)x=2x-5 (6)x2+4x≤0 (7)a+b≠c
√√×√×√√尝试反馈,巩固知识2.用不等式表示:
(1)a是正数
(2)a是负数
(3)x与3的和小于6
(4)x与2的差大于-1
(5)x的4倍大于或等于7
(6)y的一半不比3小
(7)a是非正数
(8)a是非负数a>0a<0x+3<6x-2>-14x≥7y ≥ 3尝试反馈,巩固知识 a≤0a≥0 3.用文字叙述下列不等式: 答:x的3倍大于5。答:a与4的和的两倍小于或
等于(不大于)b减去3的差.尝试反馈,巩固知识(1)3x>5(2) 2(a+4)≤b-3 思考:注意:
不等号“>”“<”表示不等关系,它们具有方向性,因而不等号两侧不可相互交换.4.用“>”或“<”填空:
(1) 4 - 6 (2) - 1 0
(3) – 8 - 3 (4) - 4.5 - 4
(5)7+3 4+3 (6)7+(-3) 4+(-3)
(7)7×3 4×3 (8)7×(-3) 4×(-3)>>>><<<< 用“>”或“<”填空:
(1)7 + 3 4 + 3 (2)7 +(-3) 4 +(-3)
(3)7×3 4×3 (4)7×(-3) 4×(-3)(1)上述不等式中哪题的不等号与7>4一致?(2)观察思考,与等式性质类比规纳出不等式
的性质.引例 >>><>>>回顾等式有哪些基本性质?1. 等式两边同时加上(或减去)
同一个数(整式), 等式仍
成立.
2. 等式两边同时乘以(或除以)
同一个数(除数不为零),
等式仍成立.1.不等式的两边都加上(或减去)同一个数,不
等号方向不变。
不等式性质变!2.不等式的两边都乘以(或除以)同一个正数
不等号方向不变。3.不等式的两边都乘以(或除以)同一个负数,
不等号方向改变。不等式性质 1如果 a < b,那么
a+c b+c ( 或 a-c b-c )不等式性质 2如果 a < b,并且 c > 0 ,那么
ac bc ( 或 )不等式性质 3如果 a < b,并且 c < 0 ,那么
ac bc ( 或 )<<<<﹥﹥变! a-3 ___ b -3 ; (2) ___ ;
(3) -4a ___ -4b . 解:(1) ∵a﹥b, ∴ a-3 ﹥b -3 (不等式性质1)(3) ∵ a﹥b, ∴ -4a ﹤-4b (不等式性质3)﹥﹥﹤ 根据不等式的基本性质,把下列不等式
化成 x ﹥ a 或 x ﹤ a 的形式 :例2 (1) x-2﹤3 ; (2) 6x ﹤5x -1; (4) -4 x ﹥ 3 . (2) 6x ﹤5x -1;
6x - 5x ﹤5x -1-5x x ﹤ -1x - 2 +2 ﹤3 +2 ,
x ﹤ 5(不等式性质1)(不等式性质1) 根据不等式的基本性质,把下列不等式
化成 x ﹥ a 或 x ﹤ a 的形式 :例2 (4) -4 x ﹥ 3 . 解:(3) (4) -4 x > 3 >>>x<(不等式性质2)(不等式性质3) 设 a ﹥ b ,用 “﹥” 或 “﹤” 号填空: a+5 ___ b +5 ; (2) 2a ___ 2b ;
(3) -5a ___ -5b ; (4) ___>><>练习一 用“>”或“<”在横线上填空,并在题后
括号内填写理由.
∵a>b (2)∵ a>b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m>5n (4)∵ >
∴ -m ( ) ∴ a 2b( )
(5)∵ 4x>5x (6)∵a-1<8
∴ x 0 ( ) ∴ a 9 ( ) ><><<< 不等式
性质1不等式
性质1不等式
性质3不等式
性质2不等式
性质1不等式
性质3练习二 (1) x+1 > 2 ; (2) 4x < 3x-5 ; 练习三2.单项选择:
(1)由 x>y 得 ax>ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(4)若 a>1,则下列各式中错误的是( )
A.4a>4 B.a+5>6 C. < D.a-1<0AD(3)由 a>b 得 am2>bm2 的条件是( )
A.m>0 B.m<0 C.m≠0 D.m是任意有理数C(2)由 x>y 得 ax≤ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0D3.判断正误:
(1)∵a+8>4 (2)∵3>2
∴a>-4 ( ) ∴3a>2a( )
(3)∵-1>-2 (4)∵ab>0
∴a-1>a-2 ( ) ∴a>0,b> 0( )√×√×1.列不等式时,要注意把表示不等关系
的词语用相应的不等号来表示.例如
“不大于”用 “≤”表示,而不用“<”
表示.练习小结注意:2.不等号方向改变不改变,要看两边都乘以
(或除以)同一个正数还是一个负数,等式
则没有这样区分。
3.不等式两边都乘以零,不等式就不成立,它将变成一个等式。而等式两边都乘以零,等式仍成立。注意:练习小结 1、试比较满足下列各
条件的m与n的大小 (1)已知m-8=n+6
(2)(m+2n) < m–n思维训练解:(1) ∵ m–n=6+8 > 0
∴ m > n
(2) ∵ m+2n <5m-2n
∴ 4n < 4m
∴ m > n 思维训练2、试讨论–8a与3a的大小解: –8 < 3
(1)当a > 0
–8a < 3a
(2)当a < 0
–8a > 3a
(3)当a =0
–8a=3a=0 思维训练3.已知不等式
(a-1)x<a-1变形得x <1.
求a的取值范围。解:∵ 不等号方向没改变
∴ a – 1 >0
∴ a >14.适合不等式∣x∣<3
的整数解有哪几个?思维训练解:由题意得:
- 3 < x < 3
整数解为:
-2,-1,0,
1,2 5 、如果a试比较a2、b2、ab、
的大小。思维训练解:∵ ab2>0
(不等式性质1)∴a2>ab>0∴0 2、互逆性(即若a>b,则b< a )
重点内容:
1. 不等式的定义
2.用不等号表示不等式(注意不等号的方向)
3.不等式的性质(注意不等式性质3)总 结A册10.1、10.2
一课一练10.1
同步10.1、10.2
作业变式训练,培养能力 6 当取下列数值时,不等式x+3>4是否成立?
-7,0,0.5,1,10 7 ①用不等式表示:
x与3的和小于或等于(不大于)6;②写出使上述不等式成立的几个的数值;③x取何值时,不等式x+3≤6总成立?取何值时不成立?再见! 不等式两边都乘以零,不等式就不成立,它将变成一个等式。注意:如果 a < b,且c = 0,那么 ac = bc
等式中“=”两侧的代数式能否交换?创设情境,复习导入 (1) 什么是等式?
回顾表示相等关系的式子。(2) 等式中“=”两侧的
代数式能否交换?能看出物体A的重量比多少克重?引导性材料(一):引导性材料(二):能看出物体A的重量比多少克轻?据气象预报,某天的最高气温是10℃,最低气温
为-5℃,由此我们说这一天的气温不低于 ℃,
并且不高于 ℃;-510引导性材料(三):不等式及
不等式的性质如:t≥-5, t≤10“≥” 是指“>”与“=”结合起来,读作“大于或 等于”,也可理解成“不小于”“≤” 是指“<”与“=”结合起来,读作“小于或 等于”,也可理解成“不大于” 用不等号(“<” “>” “≠” “≥”“≤” )表示不等关系的式子叫不等式.
不等式定义:“<” “>” “≠” “≥” “≤”认识 x>2, x <3, a <17
-7<-5, 3+4>1+4, 5+3≠12-5
a+2>a+1, x+3 <6 , a≠0,(l)上述式子中有哪些表示数量关系的符号?(2)这些符号表示什么关系?(3)这些符号两侧的代数式可以随意交换位置吗?(“<” “>” “≠” )(左右两边不相等)(除了“≠”,其余符号都不可以)1.判断下列式子哪些是不等式?为什么?
(1)3> 2 (2)a+1> 0 (3)3+2x (4)x< 2x+1 (5)x=2x-5 (6)x2+4x≤0 (7)a+b≠c
√√×√×√√尝试反馈,巩固知识2.用不等式表示:
(1)a是正数
(2)a是负数
(3)x与3的和小于6
(4)x与2的差大于-1
(5)x的4倍大于或等于7
(6)y的一半不比3小
(7)a是非正数
(8)a是非负数a>0a<0x+3<6x-2>-14x≥7y ≥ 3尝试反馈,巩固知识 a≤0a≥0 3.用文字叙述下列不等式: 答:x的3倍大于5。答:a与4的和的两倍小于或
等于(不大于)b减去3的差.尝试反馈,巩固知识(1)3x>5(2) 2(a+4)≤b-3 思考:注意:
不等号“>”“<”表示不等关系,它们具有方向性,因而不等号两侧不可相互交换.4.用“>”或“<”填空:
(1) 4 - 6 (2) - 1 0
(3) – 8 - 3 (4) - 4.5 - 4
(5)7+3 4+3 (6)7+(-3) 4+(-3)
(7)7×3 4×3 (8)7×(-3) 4×(-3)>>>><<<< 用“>”或“<”填空:
(1)7 + 3 4 + 3 (2)7 +(-3) 4 +(-3)
(3)7×3 4×3 (4)7×(-3) 4×(-3)(1)上述不等式中哪题的不等号与7>4一致?(2)观察思考,与等式性质类比规纳出不等式
的性质.引例 >>><>>>回顾等式有哪些基本性质?1. 等式两边同时加上(或减去)
同一个数(整式), 等式仍
成立.
2. 等式两边同时乘以(或除以)
同一个数(除数不为零),
等式仍成立.1.不等式的两边都加上(或减去)同一个数,不
等号方向不变。
不等式性质变!2.不等式的两边都乘以(或除以)同一个正数
不等号方向不变。3.不等式的两边都乘以(或除以)同一个负数,
不等号方向改变。不等式性质 1如果 a < b,那么
a+c b+c ( 或 a-c b-c )不等式性质 2如果 a < b,并且 c > 0 ,那么
ac bc ( 或 )不等式性质 3如果 a < b,并且 c < 0 ,那么
ac bc ( 或 )<<<<﹥﹥变! a-3 ___ b -3 ; (2) ___ ;
(3) -4a ___ -4b . 解:(1) ∵a﹥b, ∴ a-3 ﹥b -3 (不等式性质1)(3) ∵ a﹥b, ∴ -4a ﹤-4b (不等式性质3)﹥﹥﹤ 根据不等式的基本性质,把下列不等式
化成 x ﹥ a 或 x ﹤ a 的形式 :例2 (1) x-2﹤3 ; (2) 6x ﹤5x -1; (4) -4 x ﹥ 3 . (2) 6x ﹤5x -1;
6x - 5x ﹤5x -1-5x x ﹤ -1x - 2 +2 ﹤3 +2 ,
x ﹤ 5(不等式性质1)(不等式性质1) 根据不等式的基本性质,把下列不等式
化成 x ﹥ a 或 x ﹤ a 的形式 :例2 (4) -4 x ﹥ 3 . 解:(3) (4) -4 x > 3 >>>x<(不等式性质2)(不等式性质3) 设 a ﹥ b ,用 “﹥” 或 “﹤” 号填空: a+5 ___ b +5 ; (2) 2a ___ 2b ;
(3) -5a ___ -5b ; (4) ___>><>练习一 用“>”或“<”在横线上填空,并在题后
括号内填写理由.
∵a>b (2)∵ a>b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m>5n (4)∵ >
∴ -m ( ) ∴ a 2b( )
(5)∵ 4x>5x (6)∵a-1<8
∴ x 0 ( ) ∴ a 9 ( ) ><><<< 不等式
性质1不等式
性质1不等式
性质3不等式
性质2不等式
性质1不等式
性质3练习二 (1) x+1 > 2 ; (2) 4x < 3x-5 ; 练习三2.单项选择:
(1)由 x>y 得 ax>ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(4)若 a>1,则下列各式中错误的是( )
A.4a>4 B.a+5>6 C. < D.a-1<0AD(3)由 a>b 得 am2>bm2 的条件是( )
A.m>0 B.m<0 C.m≠0 D.m是任意有理数C(2)由 x>y 得 ax≤ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0D3.判断正误:
(1)∵a+8>4 (2)∵3>2
∴a>-4 ( ) ∴3a>2a( )
(3)∵-1>-2 (4)∵ab>0
∴a-1>a-2 ( ) ∴a>0,b> 0( )√×√×1.列不等式时,要注意把表示不等关系
的词语用相应的不等号来表示.例如
“不大于”用 “≤”表示,而不用“<”
表示.练习小结注意:2.不等号方向改变不改变,要看两边都乘以
(或除以)同一个正数还是一个负数,等式
则没有这样区分。
3.不等式两边都乘以零,不等式就不成立,它将变成一个等式。而等式两边都乘以零,等式仍成立。注意:练习小结 1、试比较满足下列各
条件的m与n的大小 (1)已知m-8=n+6
(2)(m+2n) < m–n思维训练解:(1) ∵ m–n=6+8 > 0
∴ m > n
(2) ∵ m+2n <5m-2n
∴ 4n < 4m
∴ m > n 思维训练2、试讨论–8a与3a的大小解: –8 < 3
(1)当a > 0
–8a < 3a
(2)当a < 0
–8a > 3a
(3)当a =0
–8a=3a=0 思维训练3.已知不等式
(a-1)x<a-1变形得x <1.
求a的取值范围。解:∵ 不等号方向没改变
∴ a – 1 >0
∴ a >14.适合不等式∣x∣<3
的整数解有哪几个?思维训练解:由题意得:
- 3 < x < 3
整数解为:
-2,-1,0,
1,2 5 、如果a试比较a2、b2、ab、
的大小。思维训练解:∵ ab2>0
(不等式性质1)∴a2>ab>0∴0
重点内容:
1. 不等式的定义
2.用不等号表示不等式(注意不等号的方向)
3.不等式的性质(注意不等式性质3)总 结A册10.1、10.2
一课一练10.1
同步10.1、10.2
作业变式训练,培养能力 6 当取下列数值时,不等式x+3>4是否成立?
-7,0,0.5,1,10 7 ①用不等式表示:
x与3的和小于或等于(不大于)6;②写出使上述不等式成立的几个的数值;③x取何值时,不等式x+3≤6总成立?取何值时不成立?再见! 不等式两边都乘以零,不等式就不成立,它将变成一个等式。注意:如果 a < b,且c = 0,那么 ac = bc
