用乘法公式分解因式(2)[下学期]
文档属性
| 名称 | 用乘法公式分解因式(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 341.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-13 00:00:00 | ||
图片预览






文档简介
课件14张PPT。6.3.2用乘法公式分解因式(二)
初一数学组
2007/03/23复习旧知利用平方差公式分解因式
(1)ax2-a
(2)16m4-n4 除了平方差公式外,你还那知道些公式?
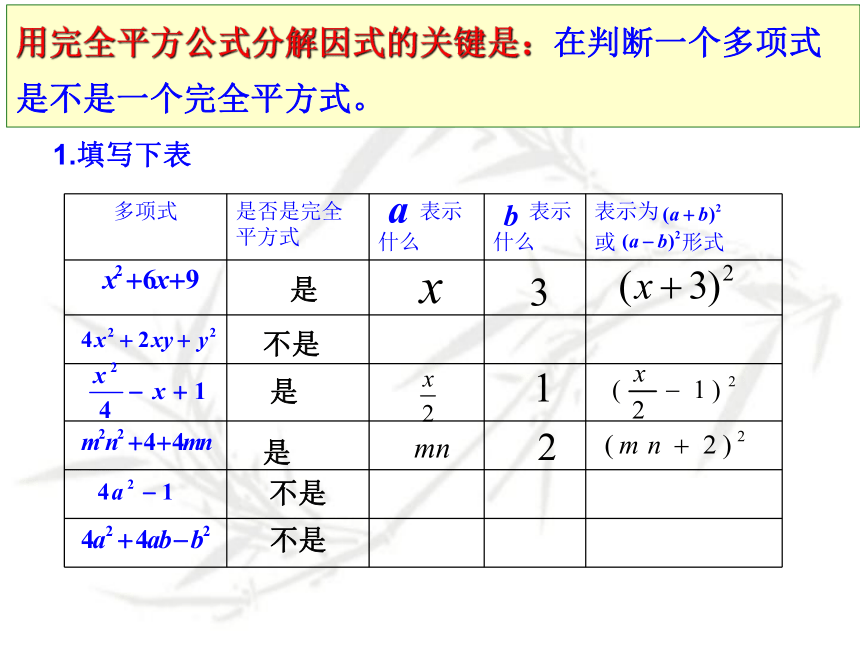
现在我们把完全平方公式反过来,可得: 两个数的平方和,加上 这两个数的积的两倍,等于这两数和 的平方.完全平方公式:(或减去)(或者差) 两个数的平方和,加上(或减去)这两个数的积的两倍,等于这两数和(或者差)的平方.形如 的多项式称为完全平方式.两个数的平方和, 加上(或减去)这两个数的积的两倍.用完全平方公式分解因式的关键是什么?用完全平方公式分解因式的关键是:在判断一个多项式是不是一个完全平方式。1.填写下表是不是是是不是不是完全平方式的特点:1.有三部分组成.2.其中有两部分分别是某两个数(或式)的平方,
且这两部分同号.3. 另一部分是上述两数(或式)的乘积的2倍,符
号可正可负.2.请补上一项,使下列多项式成为完全平方式.例1 把下列各式分解因式:若多项式中有公因式,应先提取公因式,然后再进一步分解因式。2.下面因式分解对吗?为什么?练一练:1.分解因式:例2 分解因式:练一练:把2x+y看做
a2-2ab+b2
中的字母“a”
即设a= 2x+y ,
这种数学思想称
为换元思想=(2x+y)2-2· (2x+y) ·3 +32综合练习1、用简便方法计算
(1)49.92+9.98 +0.12
(2)9 9992 +19 999
2、因式分解
(1)(4a2+1)2-16a2
(2)(a 2-2)2-4 (a2-2)+4体会.分享说一说出你这节课的收获和体验!(1)形如________________形式的多项式可以用完全平方公式分解因式。(3)因式分解要_________(2)因式分解通常优先考虑______________方法。课堂.小结提取公因式法彻底课后作业 1.请同学们设计多样化的多项式,考考你的同桌.2.作业本配套练习.
初一数学组
2007/03/23复习旧知利用平方差公式分解因式
(1)ax2-a
(2)16m4-n4 除了平方差公式外,你还那知道些公式?
现在我们把完全平方公式反过来,可得: 两个数的平方和,加上 这两个数的积的两倍,等于这两数和 的平方.完全平方公式:(或减去)(或者差) 两个数的平方和,加上(或减去)这两个数的积的两倍,等于这两数和(或者差)的平方.形如 的多项式称为完全平方式.两个数的平方和, 加上(或减去)这两个数的积的两倍.用完全平方公式分解因式的关键是什么?用完全平方公式分解因式的关键是:在判断一个多项式是不是一个完全平方式。1.填写下表是不是是是不是不是完全平方式的特点:1.有三部分组成.2.其中有两部分分别是某两个数(或式)的平方,
且这两部分同号.3. 另一部分是上述两数(或式)的乘积的2倍,符
号可正可负.2.请补上一项,使下列多项式成为完全平方式.例1 把下列各式分解因式:若多项式中有公因式,应先提取公因式,然后再进一步分解因式。2.下面因式分解对吗?为什么?练一练:1.分解因式:例2 分解因式:练一练:把2x+y看做
a2-2ab+b2
中的字母“a”
即设a= 2x+y ,
这种数学思想称
为换元思想=(2x+y)2-2· (2x+y) ·3 +32综合练习1、用简便方法计算
(1)49.92+9.98 +0.12
(2)9 9992 +19 999
2、因式分解
(1)(4a2+1)2-16a2
(2)(a 2-2)2-4 (a2-2)+4体会.分享说一说出你这节课的收获和体验!(1)形如________________形式的多项式可以用完全平方公式分解因式。(3)因式分解要_________(2)因式分解通常优先考虑______________方法。课堂.小结提取公因式法彻底课后作业 1.请同学们设计多样化的多项式,考考你的同桌.2.作业本配套练习.
