18.2.2特殊的平行四边形菱形第二课时菱形的判定课件2022--2023学年人教版八年级数学下册18张PPT
文档属性
| 名称 | 18.2.2特殊的平行四边形菱形第二课时菱形的判定课件2022--2023学年人教版八年级数学下册18张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 32.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 10:34:40 | ||
图片预览





文档简介
(共28张PPT)
18.2.2 特殊的平行四边形 菱形
第二课时 菱形的判定
第十八章 平行四边形
温故知新
1.什么是菱形?
的平行四边形叫做菱形。
2.菱形有哪些性质?
(1)菱形具有 的所有性质.
(2)菱形的四条边都 .
(3)菱形的两条对角线 ,并且每一条对角线 .
有一组对边相等
平行四边形
相等
垂直
平分一组对角
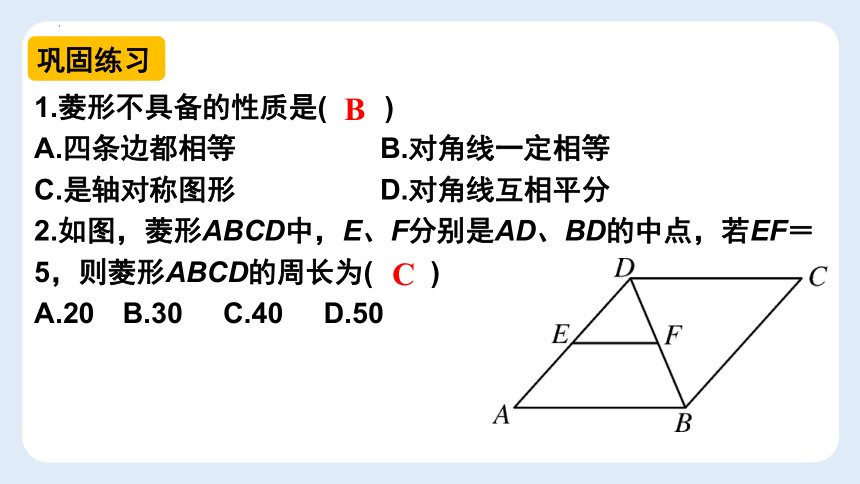
1.菱形不具备的性质是( )
A.四条边都相等 B.对角线一定相等
C.是轴对称图形 D.对角线互相平分
2.如图,菱形ABCD中,E、F分别是AD、BD的中点,若EF=5,则菱形ABCD的周长为( )
A.20 B.30 C.40 D.50
巩固练习
B
C
3.如图,菱形ABCD的对角线AC、BD相交于点O,AC=6,BD=8,且DE∥AC,AE∥BD,求OE的长.
类比矩形的判定方法,思考一下如何判定一个平行四边形是菱形?
一、菱形的判定
探索新知
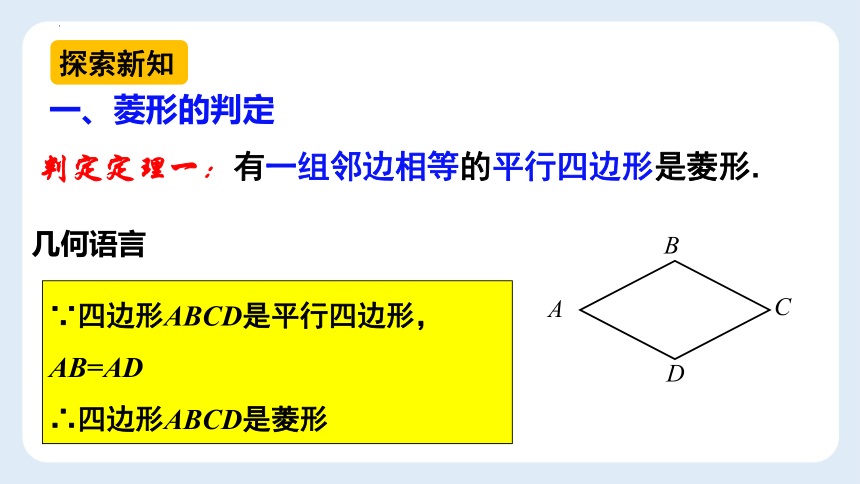
判定定理一:有一组邻边相等的平行四边形是菱形.
几何语言
A
B
C
D
∵四边形ABCD是平行四边形, AB=AD
∴四边形ABCD是菱形
猜想1.对角线互相垂直的平行四边形是菱形吗?
思考与讨论
猜想2.四条边相等的四边形是菱形吗?
活动与探究一
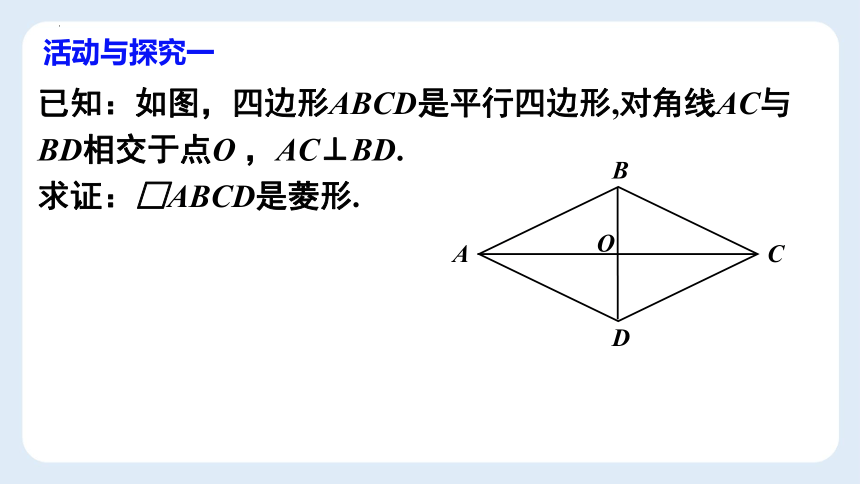
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:□ABCD是菱形.
A
B
C
O
D
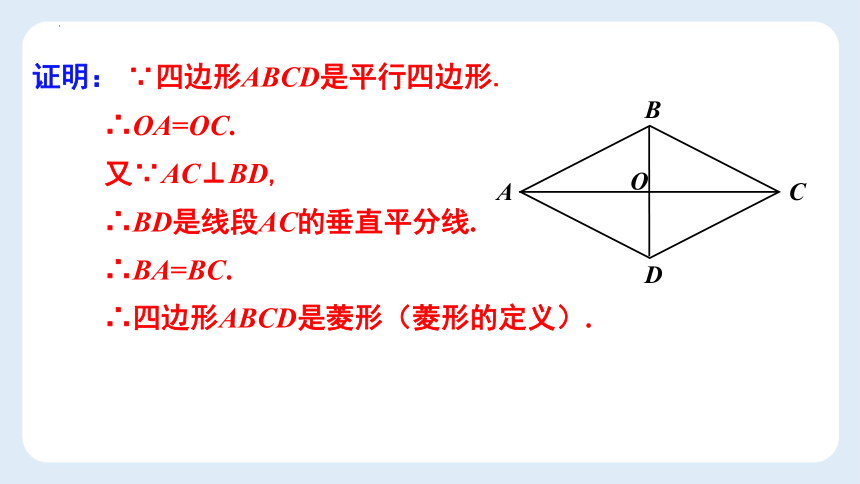
证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
A
B
C
O
D
判定定理二:对角线互相垂直的平行四边形是菱形。
几何语言
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
活动与探究二
A
B
C
D
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
判定定理三:四条边都相等的四边形是菱形。
几何语言
∵在四边形ABCD中,AB=BC=CD=AD
∴四边形 ABCD是菱形
典例精讲
【例1】 如图, ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.
又∵四边形ABCD是平行四边形,
∵ OA=4,OB=3,AB=5,
证明:
即AC⊥BD,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
∴四边形ABCD是菱形.
【例2】如图,矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
证明: ∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴ 四边形AFCE是菱形.
【例3】 如图,在△ABC中, AD是角平分线, 点E、F分别在 AB、 AD上, 且AE=AC, EF = ED.
求证:四边形CDEF是菱形.
证明: ∵ AD是角平分线, ∴∠1= ∠2.
又∵AE=AC, AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
【例3】如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A、B、C的对应点分别是D、E、F,连结AD.求证:四边形ACFD是菱形.
证明:由平移的性质,得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
【例4】如图,顺次连结矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
H
G
F
E
D
C
B
A
证明:连结AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
课堂练习
1.下列条件中,能判定□ABCD是菱形的是( )
A.AC=BD B.AB⊥BC C.AD=BD D.AC⊥BD
2.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是 ( )
A.AC⊥BD B.AB=AD
C.AC=BD D.∠ABD=∠CBD
D
C
3.如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是
( )
A.AB⊥AC B.AB=AC
C.AB=BC D.AC=BC
B
4.如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,E、F分别是AB、AC的中点.求证:四边形AEDF是菱形.
课堂小结
有一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边相等的四边形是菱形
运用定理进行计算和证明
菱形的判定
定义法
判定定理
18.2.2 特殊的平行四边形 菱形
第二课时 菱形的判定
第十八章 平行四边形
温故知新
1.什么是菱形?
的平行四边形叫做菱形。
2.菱形有哪些性质?
(1)菱形具有 的所有性质.
(2)菱形的四条边都 .
(3)菱形的两条对角线 ,并且每一条对角线 .
有一组对边相等
平行四边形
相等
垂直
平分一组对角
1.菱形不具备的性质是( )
A.四条边都相等 B.对角线一定相等
C.是轴对称图形 D.对角线互相平分
2.如图,菱形ABCD中,E、F分别是AD、BD的中点,若EF=5,则菱形ABCD的周长为( )
A.20 B.30 C.40 D.50
巩固练习
B
C
3.如图,菱形ABCD的对角线AC、BD相交于点O,AC=6,BD=8,且DE∥AC,AE∥BD,求OE的长.
类比矩形的判定方法,思考一下如何判定一个平行四边形是菱形?
一、菱形的判定
探索新知
判定定理一:有一组邻边相等的平行四边形是菱形.
几何语言
A
B
C
D
∵四边形ABCD是平行四边形, AB=AD
∴四边形ABCD是菱形
猜想1.对角线互相垂直的平行四边形是菱形吗?
思考与讨论
猜想2.四条边相等的四边形是菱形吗?
活动与探究一
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:□ABCD是菱形.
A
B
C
O
D
证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
A
B
C
O
D
判定定理二:对角线互相垂直的平行四边形是菱形。
几何语言
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
活动与探究二
A
B
C
D
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
判定定理三:四条边都相等的四边形是菱形。
几何语言
∵在四边形ABCD中,AB=BC=CD=AD
∴四边形 ABCD是菱形
典例精讲
【例1】 如图, ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.
又∵四边形ABCD是平行四边形,
∵ OA=4,OB=3,AB=5,
证明:
即AC⊥BD,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
∴四边形ABCD是菱形.
【例2】如图,矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
证明: ∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴ 四边形AFCE是菱形.
【例3】 如图,在△ABC中, AD是角平分线, 点E、F分别在 AB、 AD上, 且AE=AC, EF = ED.
求证:四边形CDEF是菱形.
证明: ∵ AD是角平分线, ∴∠1= ∠2.
又∵AE=AC, AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
【例3】如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A、B、C的对应点分别是D、E、F,连结AD.求证:四边形ACFD是菱形.
证明:由平移的性质,得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
【例4】如图,顺次连结矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
H
G
F
E
D
C
B
A
证明:连结AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
课堂练习
1.下列条件中,能判定□ABCD是菱形的是( )
A.AC=BD B.AB⊥BC C.AD=BD D.AC⊥BD
2.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是 ( )
A.AC⊥BD B.AB=AD
C.AC=BD D.∠ABD=∠CBD
D
C
3.如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是
( )
A.AB⊥AC B.AB=AC
C.AB=BC D.AC=BC
B
4.如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,E、F分别是AB、AC的中点.求证:四边形AEDF是菱形.
课堂小结
有一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边相等的四边形是菱形
运用定理进行计算和证明
菱形的判定
定义法
判定定理
