2.3 第2课时 平行线性质与判定的综合运用 课件(共18张PPT)
文档属性
| 名称 | 2.3 第2课时 平行线性质与判定的综合运用 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 376.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 18:12:53 | ||
图片预览



文档简介
(共18张PPT)
第二章 平行线与相交线
2.3 平行线的性质
第2课时 平行线的性质与判定的综合运用
北师大版 七年级下册
文字叙述 符号语言 图形
相等 两直线平行 所以a∥b
相等 两直线平行 因为 所以a∥b 互补 两直线平行 所以a∥b 同位角
内错角
同旁内角
因为∠1=∠2
∠3=∠2
因为∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
旧知回顾
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
平行于同一条直线的两条直线平行
a
b
c
图1
图形
已知
结果
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
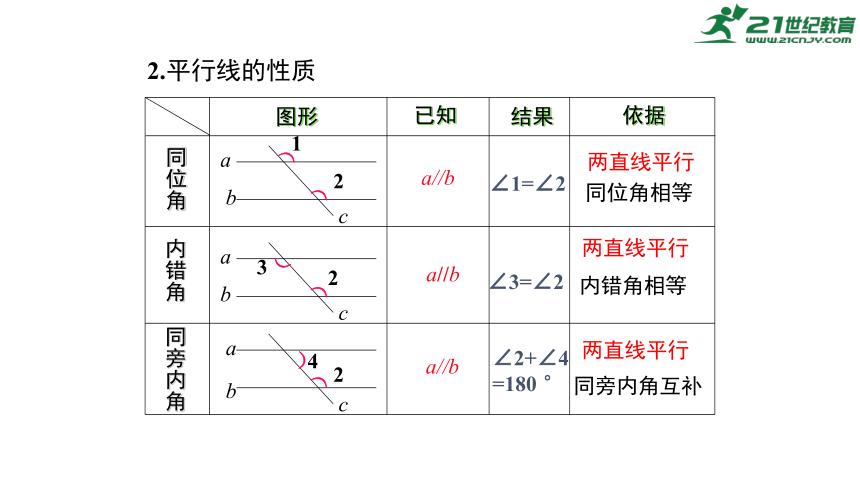
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
2.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
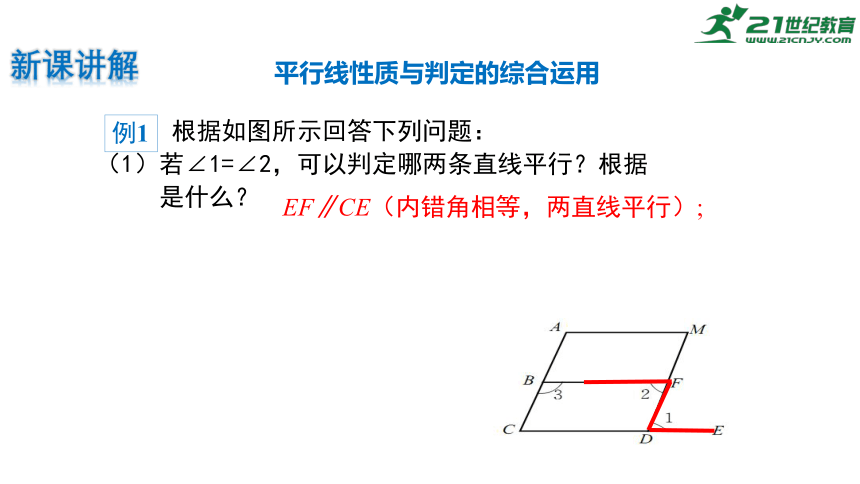
根据如图所示回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据
是什么?
EF∥CE(内错角相等,两直线平行);
新课讲解
平行线性质与判定的综合运用
例1
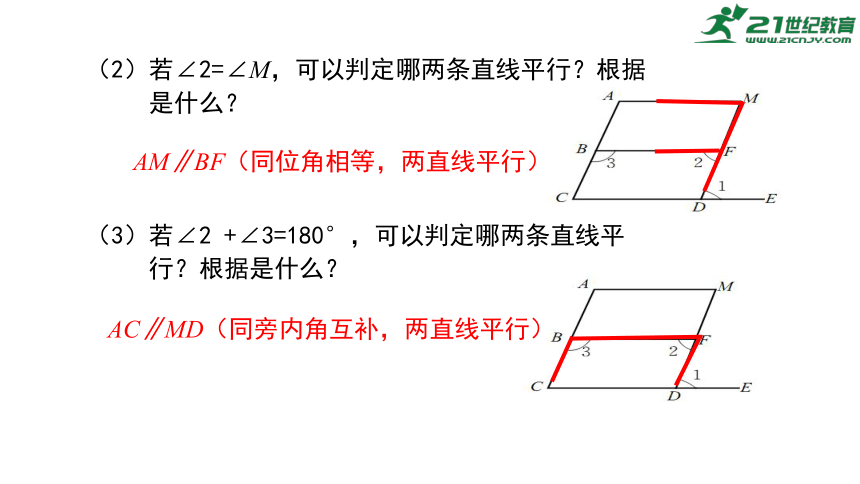
(2)若∠2=∠M,可以判定哪两条直线平行?根据
是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平
行?根据是什么?
AM∥BF(同位角相等,两直线平行)
AC∥MD(同旁内角互补,两直线平行)
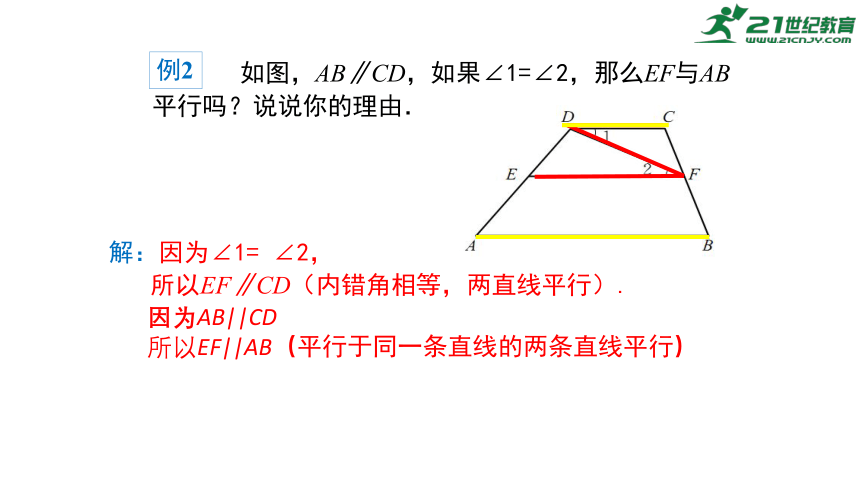
如图,AB∥CD,如果∠1=∠2,那么EF与AB
平行吗?说说你的理由.
解:因为∠1= ∠2,
例2
因为AB||CD
所以EF||AB(平行于同一条直线的两条直线平行)
所以EF∥CD(内错角相等,两直线平行).
① 因为 ∠1 =_____(已知)
所以 AB∥CE
② 因为 ∠1 +_____=180o(已知)
所以 CD∥BF
③ 因为 ∠1 +∠5 =180o(已知)
所以 _____∥_____.
AB
CE
∠2
④ 因为 ∠4 +_____=180o(已知)
所以 CE∥AB
∠3
∠3
1. 如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
练一练
如图,已知直线a∥b,直线c∥d,∠1=107°,
求∠2,∠3的度数.
.
例3
解:因为a∥b,
所以∠2=∠1=107°(两直线平行,内错角相等)
因为c∥d,
所以∠1+∠3=180°(两直线平行,同旁内角互补)
所以∠3= 180°-∠1=180°-107°=73°
解:过点E作EF//AB.
因为AB//CD,EF//AB(已知),
所以 CD//EF(平行于同一直线的两直线平行).
所以∠A+∠1 =180o,∠C+∠ 2 =180o(两直线平行,同旁内角互补).
又因为∠A=100°,∠C=110°(已知),
所以∠ 1 =80°, ∠2 =70°(等量代换).
所以∠AEC=∠1+∠2= 80°+70° = 150 °.
如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC
的度数.
E
A
B
C
D
2
1
F
例4
如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC
的度数.
E
A
B
C
D
F
例4
因为 AB||CD
所以 ∠A+∠AFC=180°(两直线平行,同旁内角互补)
因为∠A=100°
所以 ∠AFC=180°-100°=80°
因为 ∠ACE=110°
所以 ∠ECF=180°-110°=70°(邻补角的定义)
在△EFC中,∠FEC=180°-∠EFC-∠ECF=180°-80°-70°=30°
所以∠AEC=180°-∠FEC=180°-30°=150°
解:延长AE交直线CD于点F
如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC
的度数.
E
A
B
C
D
F
例4
解:过点C作直线CF交AB于点F
因为AB||CD
所以∠AFC=∠FCD(两直线平行,内错角相等)
在四边形AECF中 ∠A=100° ∠ECD=110°
∠AEC=360°-∠A-∠ECF-∠AFC=360°-∠A-∠ECF-∠FCD
=360°-∠A-(∠ECF+∠FCD)=360°-∠A-∠ECD
=360°-100°-110°=150°
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
角的关系
线的关系
课堂小结
1.如图,∠A=∠D,如果∠B=20°,那么∠C
为( )
A.40° B.20°
C.60° D.70°
B
课堂检测
2.如图,直线a,b与直线c,d相交,若∠1=∠2,
∠3=70°,则∠4的度数是( )
A.35° B.70°
C.90° D.110°
D
3.如图,AE∥CD,若∠1=37°,∠D=54°,求∠2
和∠BAE的度数.
解:因为AE∥CD,
所以∠2=∠1=37°(两直线平行,内错角相等)
所以∠BAE=∠D=54°(两直线平行,同位角相等)
4.一大门的栏杆如图所示,BA垂直于地面AE于
A,CD平行于地面AE,则∠ABC+∠BCD=
______度.
方法一:过B作BF∥AE,
则CD∥BF∥AE.
270
方法二:延长CB于AE相交
方法三:过点C作CH⊥AE
H
5.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:
因为∠1=∠2
所以AB∥EF
(内错角相等,两直线平行).
因为AB⊥BF,CD⊥BF,
所以AB∥CD(同位角相等,两直线平行)
所以EF∥CD
所以 ∠3= ∠E
(平行于同一条直线的两条直线平行).
(两直线平行,内错角相等).
所以 ∠B=∠CDF=90°
第二章 平行线与相交线
2.3 平行线的性质
第2课时 平行线的性质与判定的综合运用
北师大版 七年级下册
文字叙述 符号语言 图形
相等 两直线平行 所以a∥b
相等 两直线平行 因为 所以a∥b 互补 两直线平行 所以a∥b 同位角
内错角
同旁内角
因为∠1=∠2
∠3=∠2
因为∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
旧知回顾
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
平行于同一条直线的两条直线平行
a
b
c
图1
图形
已知
结果
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
2.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
根据如图所示回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据
是什么?
EF∥CE(内错角相等,两直线平行);
新课讲解
平行线性质与判定的综合运用
例1
(2)若∠2=∠M,可以判定哪两条直线平行?根据
是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平
行?根据是什么?
AM∥BF(同位角相等,两直线平行)
AC∥MD(同旁内角互补,两直线平行)
如图,AB∥CD,如果∠1=∠2,那么EF与AB
平行吗?说说你的理由.
解:因为∠1= ∠2,
例2
因为AB||CD
所以EF||AB(平行于同一条直线的两条直线平行)
所以EF∥CD(内错角相等,两直线平行).
① 因为 ∠1 =_____(已知)
所以 AB∥CE
② 因为 ∠1 +_____=180o(已知)
所以 CD∥BF
③ 因为 ∠1 +∠5 =180o(已知)
所以 _____∥_____.
AB
CE
∠2
④ 因为 ∠4 +_____=180o(已知)
所以 CE∥AB
∠3
∠3
1. 如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
练一练
如图,已知直线a∥b,直线c∥d,∠1=107°,
求∠2,∠3的度数.
.
例3
解:因为a∥b,
所以∠2=∠1=107°(两直线平行,内错角相等)
因为c∥d,
所以∠1+∠3=180°(两直线平行,同旁内角互补)
所以∠3= 180°-∠1=180°-107°=73°
解:过点E作EF//AB.
因为AB//CD,EF//AB(已知),
所以 CD//EF(平行于同一直线的两直线平行).
所以∠A+∠1 =180o,∠C+∠ 2 =180o(两直线平行,同旁内角互补).
又因为∠A=100°,∠C=110°(已知),
所以∠ 1 =80°, ∠2 =70°(等量代换).
所以∠AEC=∠1+∠2= 80°+70° = 150 °.
如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC
的度数.
E
A
B
C
D
2
1
F
例4
如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC
的度数.
E
A
B
C
D
F
例4
因为 AB||CD
所以 ∠A+∠AFC=180°(两直线平行,同旁内角互补)
因为∠A=100°
所以 ∠AFC=180°-100°=80°
因为 ∠ACE=110°
所以 ∠ECF=180°-110°=70°(邻补角的定义)
在△EFC中,∠FEC=180°-∠EFC-∠ECF=180°-80°-70°=30°
所以∠AEC=180°-∠FEC=180°-30°=150°
解:延长AE交直线CD于点F
如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC
的度数.
E
A
B
C
D
F
例4
解:过点C作直线CF交AB于点F
因为AB||CD
所以∠AFC=∠FCD(两直线平行,内错角相等)
在四边形AECF中 ∠A=100° ∠ECD=110°
∠AEC=360°-∠A-∠ECF-∠AFC=360°-∠A-∠ECF-∠FCD
=360°-∠A-(∠ECF+∠FCD)=360°-∠A-∠ECD
=360°-100°-110°=150°
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
角的关系
线的关系
课堂小结
1.如图,∠A=∠D,如果∠B=20°,那么∠C
为( )
A.40° B.20°
C.60° D.70°
B
课堂检测
2.如图,直线a,b与直线c,d相交,若∠1=∠2,
∠3=70°,则∠4的度数是( )
A.35° B.70°
C.90° D.110°
D
3.如图,AE∥CD,若∠1=37°,∠D=54°,求∠2
和∠BAE的度数.
解:因为AE∥CD,
所以∠2=∠1=37°(两直线平行,内错角相等)
所以∠BAE=∠D=54°(两直线平行,同位角相等)
4.一大门的栏杆如图所示,BA垂直于地面AE于
A,CD平行于地面AE,则∠ABC+∠BCD=
______度.
方法一:过B作BF∥AE,
则CD∥BF∥AE.
270
方法二:延长CB于AE相交
方法三:过点C作CH⊥AE
H
5.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:
因为∠1=∠2
所以AB∥EF
(内错角相等,两直线平行).
因为AB⊥BF,CD⊥BF,
所以AB∥CD(同位角相等,两直线平行)
所以EF∥CD
所以 ∠3= ∠E
(平行于同一条直线的两条直线平行).
(两直线平行,内错角相等).
所以 ∠B=∠CDF=90°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
