鲁教版八年级数学上册期末测试试题(2)(含答案)
文档属性
| 名称 | 鲁教版八年级数学上册期末测试试题(2)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 358.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 16:41:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
鲁教版上学期期末质量检测二
八年级数学试题
第Ⅰ卷(选择题 共36分)
一、选择题(每小题3分,共36分)
1.若多项式-12x2y3+16x3y2+4x2y2分解因式,其中一个因式是-4x2y2,则另一个因式是( )
A.3y+4x-1 B.3y-4x-1 C.3y-4x+1 D.3y-4x
2.将分式中的x、y的值同时扩大2倍,则分式的值( )
A.扩大2倍 B.缩小到原来的 C.保持不变 D.无法确定
3.已知关于x的方程 无解,则a的值是( )
A.2 B.1 C.-1 D.不存在
4.若分式的值为0,则x的值为( )
A.x=-1或x=2 B、x=0 C.x=2 D.x=-1
5.若m>-1,则多项式m3-m2-m+1的值为( )
A. 正数 B. 负数 C. 非负数 D. 非正数
6.下列运动形式属于旋转的是( )
A.在空中上升的氢气球 B.飞驰的火车
C.时钟上钟摆的摆动 D.运动员掷出的标枪
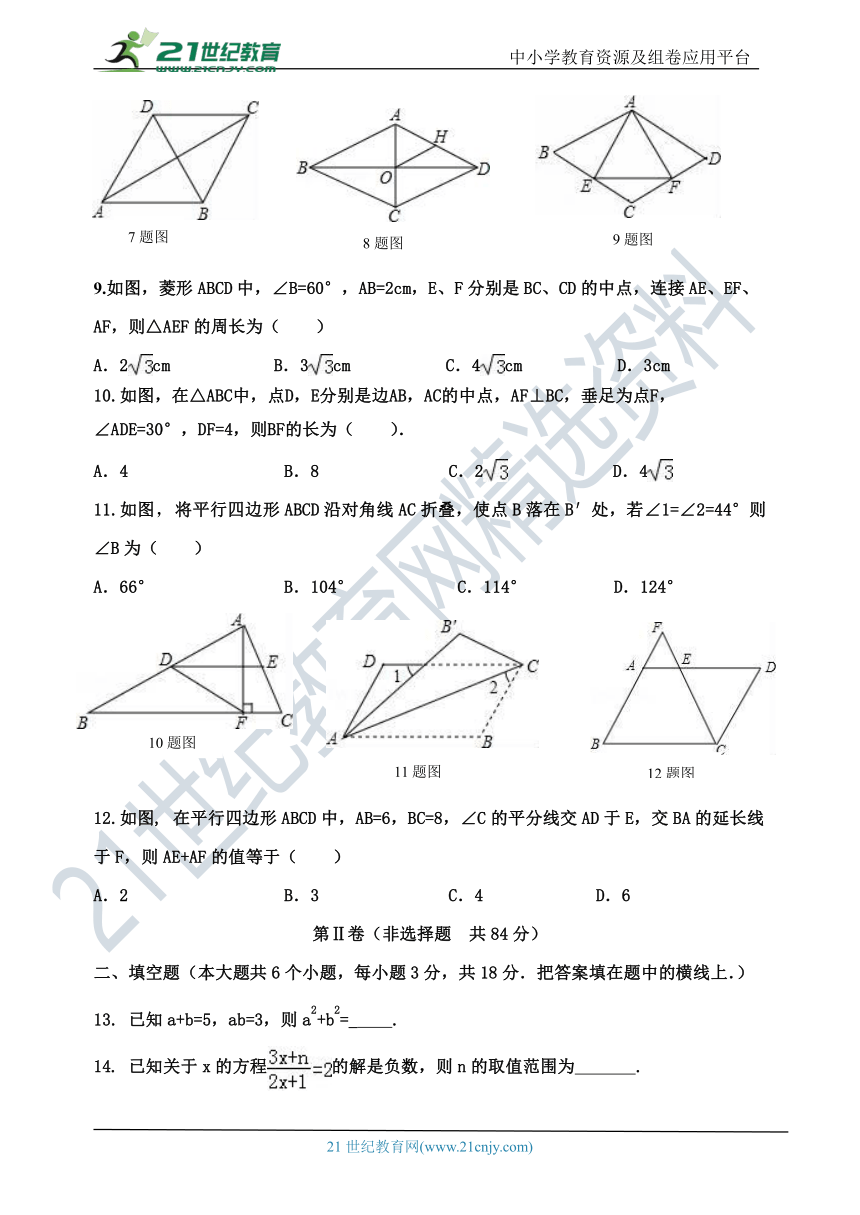
7.如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6米 B.6米 C.3米 D.3米
8.如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于( )
A.3.5 B.4 C.7 D.14
9.如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )
A.2cm B.3cm C.4cm D.3cm
10.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,
∠ADE=30°,DF=4,则BF的长为( ).
A.4 B.8 C.2 D.4
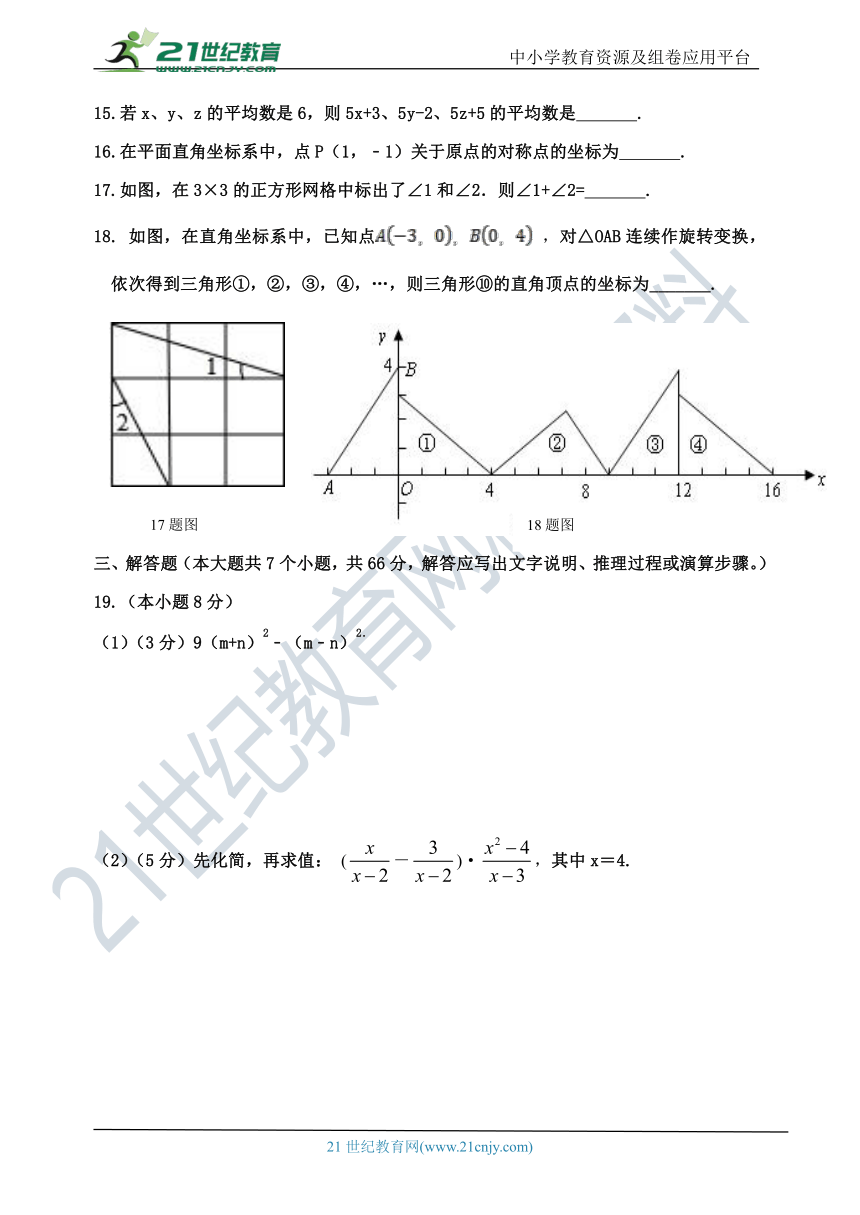
11.如图,将平行四边形ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°则∠B为( )
A.66° B.104° C.114° D.124°
12.如图, 在平行四边形ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2 B.3 C.4 D.6
第Ⅱ卷(非选择题 共84分)
二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中的横线上.)
13. 已知a+b=5,ab=3,则a2+b2=_ .
14. 已知关于x的方程的解是负数,则n的取值范围为 .
15.若x、y、z的平均数是6,则5x+3、5y-2、5z+5的平均数是 .
16.在平面直角坐标系中,点P(1,﹣1)关于原点的对称点的坐标为 .
17.如图,在3×3的正方形网格中标出了∠1和∠2.则∠1+∠2= .
18. 如图,在直角坐标系中,已知点 ,对△OAB连续作旋转变换,依次得到三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为_______.
三、解答题(本大题共7个小题,共66分,解答应写出文字说明、推理过程或演算步骤。)
19.(本小题8分)
(1)(3分)9(m+n)2﹣(m﹣n)2.
(2)(5分)先化简,再求值: (-)·,其中x=4.
20.(本小题8分)某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
21.(本小题8分)
某公司招聘一名员工,对甲、乙、丙三名应聘者进行三项素质测试,各项测试成绩如下表:
测试项目 测试成绩
甲 乙 丙
创新 8 9 7
综合知识 5 7 7
语言 9 5 7
(1)如果根据三项成绩的平均分确定录用人选,那么应该选谁?
(2)根据实际需要,公司将创新、综合知识和语言三项得分按3:2:1的比例确定最终人选,那么如何确定人选?
22.(本小题8分)
如图,E是等边三角形ABC内的一点,且EA=5,EB=12,EC=13.若将△AEC绕点A按逆时针方向旋转后,得到△ADB.
求①求线段DE的长度
②求∠AEB的度数
23.(本小题10分)
如图,平行四边形ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
(1)求证:四边形CMAN是平行四边形.
(2)已知DE=4,FN=3,求BN的长.
24.(本小题12分)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
25.(本小题12分)如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且,PA=PE,PE交CD于点F,
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,试探究线段AP与线段CE的数量关系,并说明理由。
鲁教版上学期期末质量检测二
八年级数学参考答案
一、选择题(本大题共12个小题,每小题3分,共36分.)
BABCC CAABD CC
二、填空题(本大题共6个小题,每小题3分,共18分。)
13. 19 , 14. n<2且n≠ ,15.32,16. (﹣1,1), 17. 45°,18.(36.0)
三、解答题
19.(1) 原式=[3(m+n)+(m﹣n)][3(m+n)﹣(m﹣n)]=4(2m+n)(m+2n).
(2)(-)·=·=x+2.
当x=4时,原式=6.
20.解:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元,由题意,得=2×+300,解得x=5,经检验x=5是方程的解.
答:该种干果的第一次进价是每千克5元;
(2)[+﹣600]×9+600×9×80%﹣(3000+9000)=(600+1500﹣600)×9+4320﹣12000=1500×9+4320﹣12000=13500+4320﹣12000=5820(元).
答:超市销售这种干果共盈利5820元.
21.解:(1)甲的为:(8+5+9)÷3=,乙的为:(9+7+5)÷3=7,
丙的为:(7+7+7)÷3=7甲将被录用;
(2)解:甲成绩=(8×3+5×2+9×1)÷6≈7.17,乙成绩=(9×3+7×2+5×1)÷6≈7.67,
丙成绩=(7×3+7×2+7×1)÷6=7,乙将被录取.
22. 解:①连接将DE,△AEC绕点A按逆时针方向旋转后得到△ADB∴∠EAC=∠DAB ,AD=AE
∴∠BAC=∠DAE又∵△ABC为等边三角形∴∠DAE=60°∴△ADE为等边三角形,又∵AE=5∴DE=5
②△AEC绕点A按逆时针方向旋转后得到△ADB∴BD=EC=13,在△EDB,DE2+BE2=BD2.
∴∠DEB=90°又∵∠DAE=60°∴∠AEB =150°
23.(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,∵AM⊥BD,CN⊥BD,
∴AM∥CN,∴CM∥AN,AM∥CN,∴四边形AMCN是平行四边形.
(2)∵四边形AMCN是平行四边形,∴CM=AN,∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB,∴DM=BN,∠MDE=∠NBF,在△MDE和△NBF中,
,
∴△MDE≌△NBF,∴ME=NF=3,在Rt△DME中,∵∠DEM=90°,DE=4,ME=3,
∴DM===5,∴BN=DM=5.
24.解:(1)BD=CD.理由如下:依题意得AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,∵AB=AC,BD=CD,∴∠ADB=90°,∴四边形AFBD是矩形.
25.(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45 ,在△ABP和△CBP中,AB=BC,∠ABP=∠CBP,PB=PB,∴△ABP≌△CBP(SAS),∴PA=PC,∵PA=PE,∴PC=PE;
(2)由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP,∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E,∵∠CFP=∠EFD,∴180 ∠PFC ∠PCF=180 ∠DFE ∠E,
即∠CPF=∠EDF=90
(3)AP=CE;理由如下:在菱形ABCD中,AB=BC,∠ABP=∠CBP=60 ,在△ABP和△CBP中,AB=BC,∠ABP=∠CBP,PB=PB,∴△ABP≌△CBP(SAS),∴PA=PC,∠BAP=∠BCP,∵PA=PE,∴PC=PE,∴∠DAP=∠DCP,∵PA=PC,∴∠DAP=∠AEP,∴∠DCP=∠AEP∵∠CFP=∠EFD(对顶角相等),
∴180 ∠PFC ∠PCF=180 ∠DFE ∠AEP,即∠CPF=∠EDF=180 ∠ADC=180 120 =60
∴△EPC是等边三角形,∴PC=CE,∴AP=CE.
9题图
8题图
7题图
10题图
11题图
12题图
18题图
17题图
A
D
B
C
E
第22题图
23题图
24题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
鲁教版上学期期末质量检测二
八年级数学试题
第Ⅰ卷(选择题 共36分)
一、选择题(每小题3分,共36分)
1.若多项式-12x2y3+16x3y2+4x2y2分解因式,其中一个因式是-4x2y2,则另一个因式是( )
A.3y+4x-1 B.3y-4x-1 C.3y-4x+1 D.3y-4x
2.将分式中的x、y的值同时扩大2倍,则分式的值( )
A.扩大2倍 B.缩小到原来的 C.保持不变 D.无法确定
3.已知关于x的方程 无解,则a的值是( )
A.2 B.1 C.-1 D.不存在
4.若分式的值为0,则x的值为( )
A.x=-1或x=2 B、x=0 C.x=2 D.x=-1
5.若m>-1,则多项式m3-m2-m+1的值为( )
A. 正数 B. 负数 C. 非负数 D. 非正数
6.下列运动形式属于旋转的是( )
A.在空中上升的氢气球 B.飞驰的火车
C.时钟上钟摆的摆动 D.运动员掷出的标枪
7.如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6米 B.6米 C.3米 D.3米
8.如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于( )
A.3.5 B.4 C.7 D.14
9.如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )
A.2cm B.3cm C.4cm D.3cm
10.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,
∠ADE=30°,DF=4,则BF的长为( ).
A.4 B.8 C.2 D.4
11.如图,将平行四边形ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°则∠B为( )
A.66° B.104° C.114° D.124°
12.如图, 在平行四边形ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2 B.3 C.4 D.6
第Ⅱ卷(非选择题 共84分)
二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中的横线上.)
13. 已知a+b=5,ab=3,则a2+b2=_ .
14. 已知关于x的方程的解是负数,则n的取值范围为 .
15.若x、y、z的平均数是6,则5x+3、5y-2、5z+5的平均数是 .
16.在平面直角坐标系中,点P(1,﹣1)关于原点的对称点的坐标为 .
17.如图,在3×3的正方形网格中标出了∠1和∠2.则∠1+∠2= .
18. 如图,在直角坐标系中,已知点 ,对△OAB连续作旋转变换,依次得到三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为_______.
三、解答题(本大题共7个小题,共66分,解答应写出文字说明、推理过程或演算步骤。)
19.(本小题8分)
(1)(3分)9(m+n)2﹣(m﹣n)2.
(2)(5分)先化简,再求值: (-)·,其中x=4.
20.(本小题8分)某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
21.(本小题8分)
某公司招聘一名员工,对甲、乙、丙三名应聘者进行三项素质测试,各项测试成绩如下表:
测试项目 测试成绩
甲 乙 丙
创新 8 9 7
综合知识 5 7 7
语言 9 5 7
(1)如果根据三项成绩的平均分确定录用人选,那么应该选谁?
(2)根据实际需要,公司将创新、综合知识和语言三项得分按3:2:1的比例确定最终人选,那么如何确定人选?
22.(本小题8分)
如图,E是等边三角形ABC内的一点,且EA=5,EB=12,EC=13.若将△AEC绕点A按逆时针方向旋转后,得到△ADB.
求①求线段DE的长度
②求∠AEB的度数
23.(本小题10分)
如图,平行四边形ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
(1)求证:四边形CMAN是平行四边形.
(2)已知DE=4,FN=3,求BN的长.
24.(本小题12分)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
25.(本小题12分)如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且,PA=PE,PE交CD于点F,
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,试探究线段AP与线段CE的数量关系,并说明理由。
鲁教版上学期期末质量检测二
八年级数学参考答案
一、选择题(本大题共12个小题,每小题3分,共36分.)
BABCC CAABD CC
二、填空题(本大题共6个小题,每小题3分,共18分。)
13. 19 , 14. n<2且n≠ ,15.32,16. (﹣1,1), 17. 45°,18.(36.0)
三、解答题
19.(1) 原式=[3(m+n)+(m﹣n)][3(m+n)﹣(m﹣n)]=4(2m+n)(m+2n).
(2)(-)·=·=x+2.
当x=4时,原式=6.
20.解:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元,由题意,得=2×+300,解得x=5,经检验x=5是方程的解.
答:该种干果的第一次进价是每千克5元;
(2)[+﹣600]×9+600×9×80%﹣(3000+9000)=(600+1500﹣600)×9+4320﹣12000=1500×9+4320﹣12000=13500+4320﹣12000=5820(元).
答:超市销售这种干果共盈利5820元.
21.解:(1)甲的为:(8+5+9)÷3=,乙的为:(9+7+5)÷3=7,
丙的为:(7+7+7)÷3=7甲将被录用;
(2)解:甲成绩=(8×3+5×2+9×1)÷6≈7.17,乙成绩=(9×3+7×2+5×1)÷6≈7.67,
丙成绩=(7×3+7×2+7×1)÷6=7,乙将被录取.
22. 解:①连接将DE,△AEC绕点A按逆时针方向旋转后得到△ADB∴∠EAC=∠DAB ,AD=AE
∴∠BAC=∠DAE又∵△ABC为等边三角形∴∠DAE=60°∴△ADE为等边三角形,又∵AE=5∴DE=5
②△AEC绕点A按逆时针方向旋转后得到△ADB∴BD=EC=13,在△EDB,DE2+BE2=BD2.
∴∠DEB=90°又∵∠DAE=60°∴∠AEB =150°
23.(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,∵AM⊥BD,CN⊥BD,
∴AM∥CN,∴CM∥AN,AM∥CN,∴四边形AMCN是平行四边形.
(2)∵四边形AMCN是平行四边形,∴CM=AN,∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB,∴DM=BN,∠MDE=∠NBF,在△MDE和△NBF中,
,
∴△MDE≌△NBF,∴ME=NF=3,在Rt△DME中,∵∠DEM=90°,DE=4,ME=3,
∴DM===5,∴BN=DM=5.
24.解:(1)BD=CD.理由如下:依题意得AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,∵AB=AC,BD=CD,∴∠ADB=90°,∴四边形AFBD是矩形.
25.(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45 ,在△ABP和△CBP中,AB=BC,∠ABP=∠CBP,PB=PB,∴△ABP≌△CBP(SAS),∴PA=PC,∵PA=PE,∴PC=PE;
(2)由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP,∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E,∵∠CFP=∠EFD,∴180 ∠PFC ∠PCF=180 ∠DFE ∠E,
即∠CPF=∠EDF=90
(3)AP=CE;理由如下:在菱形ABCD中,AB=BC,∠ABP=∠CBP=60 ,在△ABP和△CBP中,AB=BC,∠ABP=∠CBP,PB=PB,∴△ABP≌△CBP(SAS),∴PA=PC,∠BAP=∠BCP,∵PA=PE,∴PC=PE,∴∠DAP=∠DCP,∵PA=PC,∴∠DAP=∠AEP,∴∠DCP=∠AEP∵∠CFP=∠EFD(对顶角相等),
∴180 ∠PFC ∠PCF=180 ∠DFE ∠AEP,即∠CPF=∠EDF=180 ∠ADC=180 120 =60
∴△EPC是等边三角形,∴PC=CE,∴AP=CE.
9题图
8题图
7题图
10题图
11题图
12题图
18题图
17题图
A
D
B
C
E
第22题图
23题图
24题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
