期中综合质量模拟检测卷 2022-2023学年人教版数学九年级下册(含答案)
文档属性
| 名称 | 期中综合质量模拟检测卷 2022-2023学年人教版数学九年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 818.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 12:35:16 | ||
图片预览


文档简介
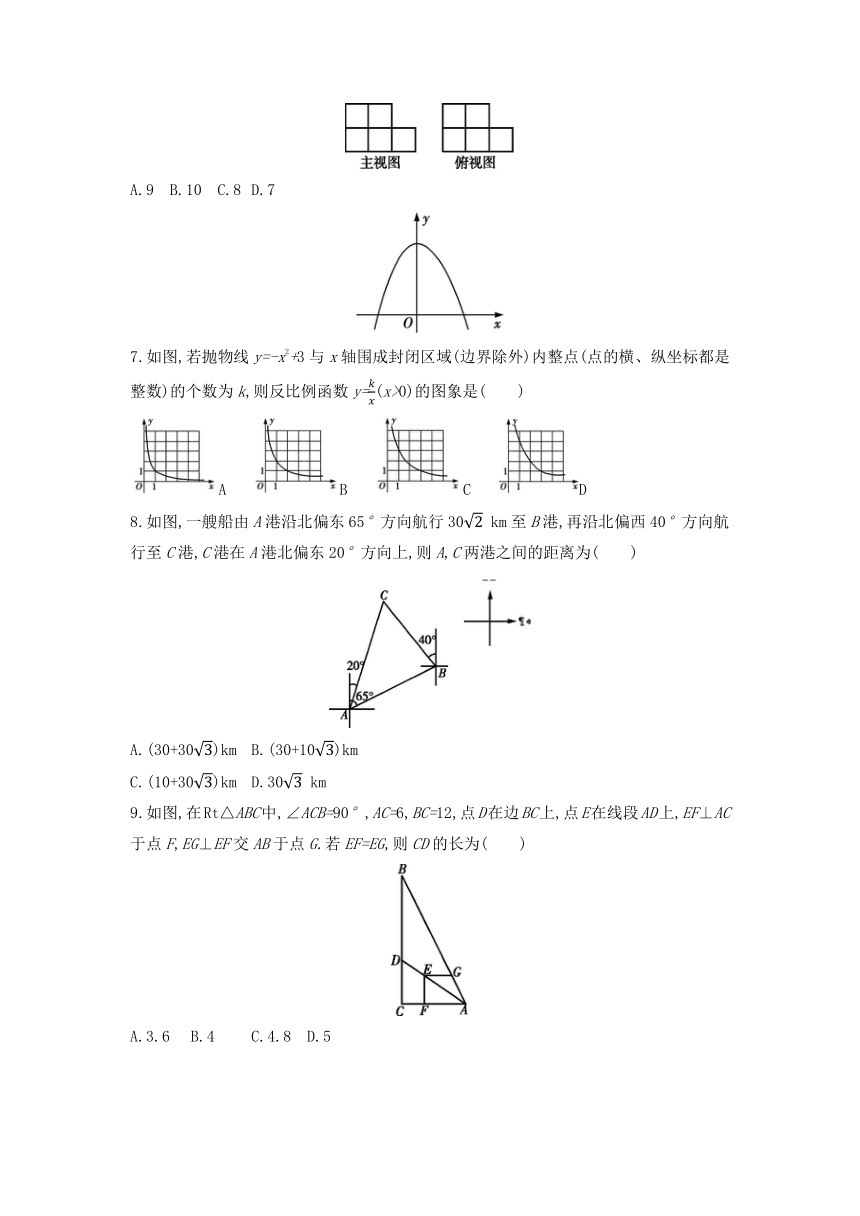
期中综合质量模拟检测卷
时间:90分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.下列选项中的点在反比例函数y=图象上的是( )
A.(2,3) B.(4,2) C.(-6,1) D.(-2,3)
2.下列四幅图,表示两棵树在同一时刻阳光下的影子的是( )
A B C D
3.如图,在平面直角坐标系中,从原点O引一条射线,设这条射线与x轴的正半轴的夹角为α,若cos α=,则这条射线是( )
A.OA B.OB C.OC D.OD
(第3题) (第4题)
4.如图,已知点D,E是AB边上的三等分点,线段DF,EG将△ABC分成三部分,且DF∥EG∥BC,图中三部分的面积分别为S1,S2,S3,则S1∶S2∶S3=( )
A.1∶2∶3 B.1∶2∶4 C.1∶3∶5 D.2∶3∶4
5.如图,在平面直角坐标系中,以P(4,6)为位似中心,把△ABC缩小得到△DEF,若变换后,点A,B的对应点分别为点D,E,则点C的对应点F的坐标应为( )
A.(4,2) B.(4,4) C.(4,5) D.(5,4)
6.已知一个组合体是由几个相同的正方体叠合在一起组成的,该组合体的主视图与俯视图如图所示,则该组合体中正方体的个数最多是( )
A.9 B.10 C.8 D.7
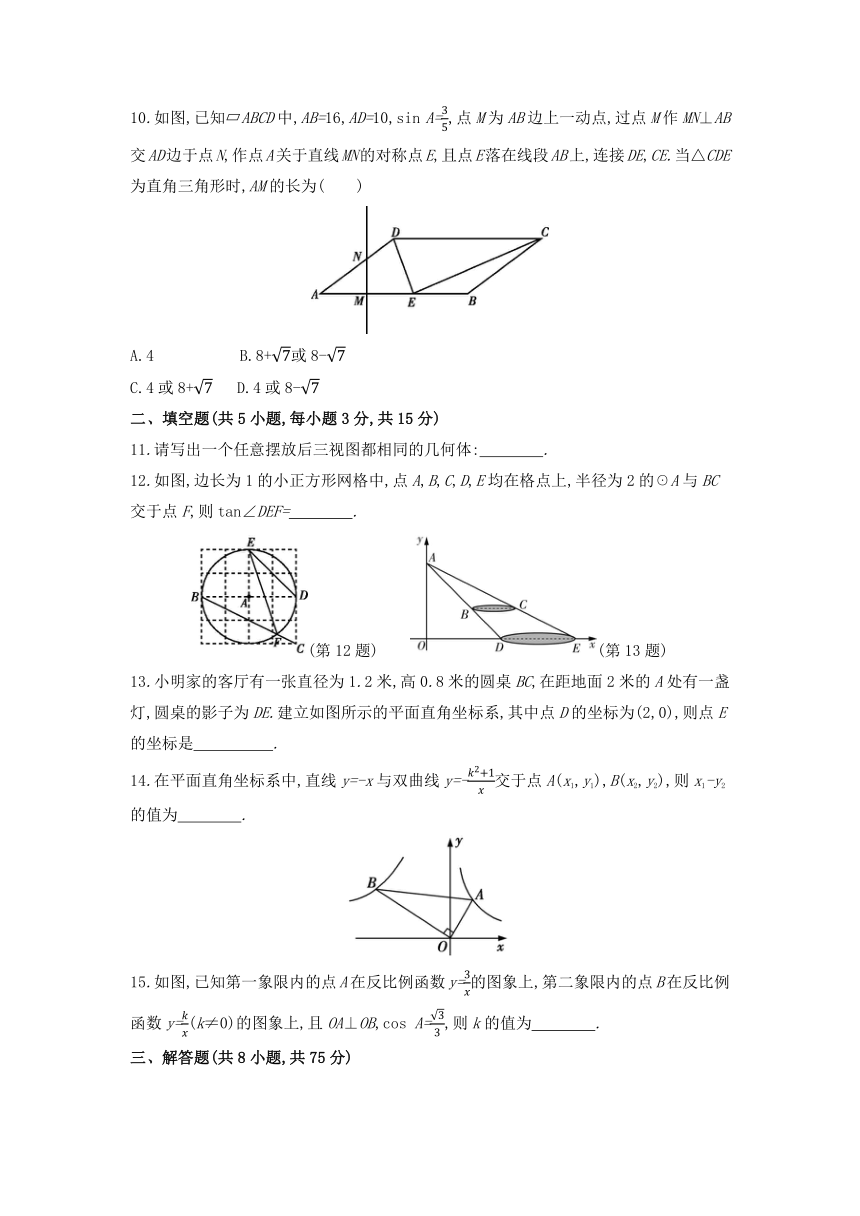
7.如图,若抛物线y=-x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k,则反比例函数y=(x>0)的图象是( )
A B C D
8.如图,一艘船由A港沿北偏东65°方向航行30 km至B港,再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向上,则A,C两港之间的距离为( )
A.(30+30)km B.(30+10)km
C.(10+30)km D.30 km
9.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( )
A.3.6 B.4 C.4.8 D.5
10.如图,已知 ABCD中,AB=16,AD=10,sin A=,点M为AB边上一动点,过点M作MN⊥AB交AD边于点N,作点A关于直线MN的对称点E,且点E落在线段AB上,连接DE,CE.当△CDE为直角三角形时,AM的长为( )
A.4 B.8+或8-
C.4或8+ D.4或8-
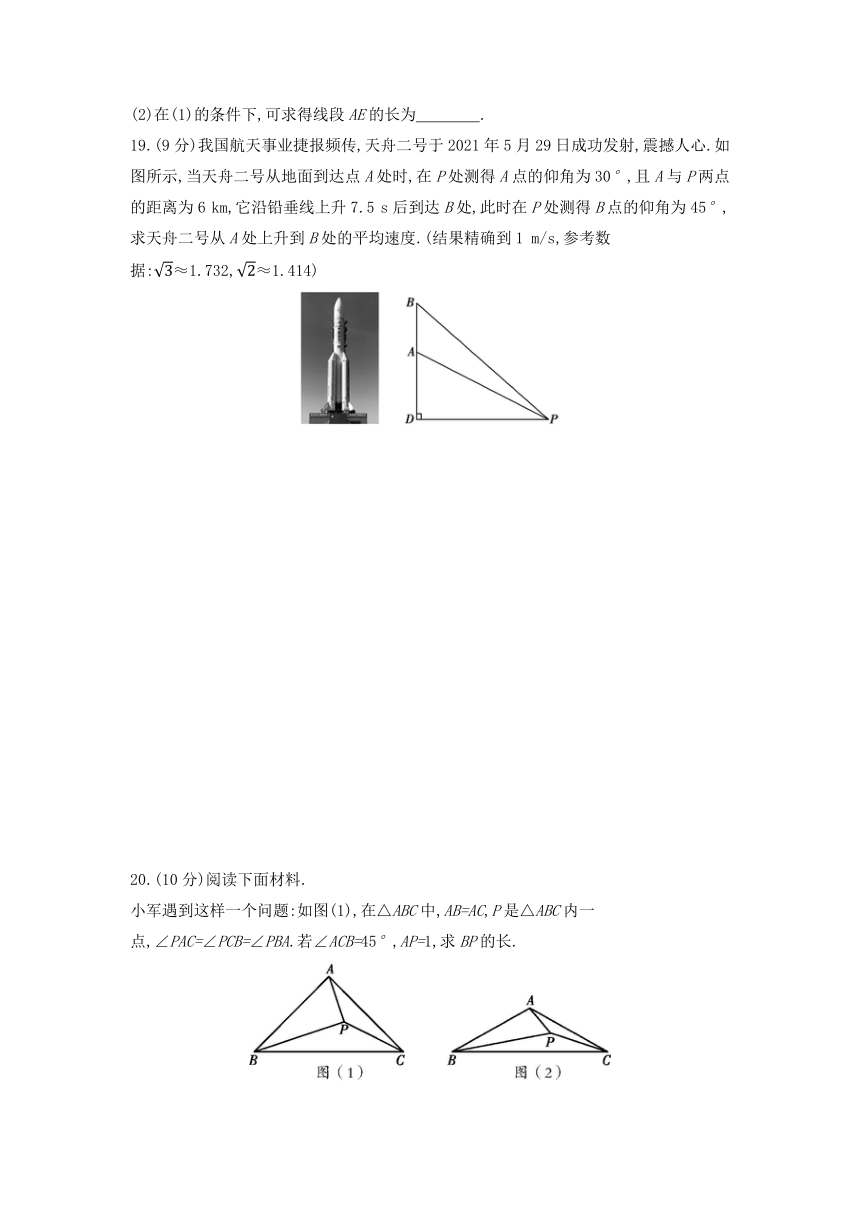
二、填空题(共5小题,每小题3分,共15分)
11.请写出一个任意摆放后三视图都相同的几何体: .
12.如图,边长为1的小正方形网格中,点A,B,C,D,E均在格点上,半径为2的☉A与BC交于点F,则tan∠DEF= .
(第12题) (第13题)
13.小明家的客厅有一张直径为1.2米,高0.8米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE.建立如图所示的平面直角坐标系,其中点D的坐标为(2,0),则点E的坐标是 .
14.在平面直角坐标系中,直线y=-x与双曲线y=-交于点A(x1,y1),B(x2,y2),则x1-y2的值为 .
15.如图,已知第一象限内的点A在反比例函数y=的图象上,第二象限内的点B在反比例函数y=(k≠0)的图象上,且OA⊥OB,cos A=,则k的值为 .
三、解答题(共8小题,共75分)
16.(7分)如图,已知在Rt△ABC中,∠C=90°,AC=3,BC=4.求tan Bsin A+|1-cos B|+的值.
17.(7分)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该函数的解析式;
(2)当气球内的气压大于140 kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少 (精确到0.01 m3)
18.(8分)如图,在矩形ABCD中,AB=4,BC=6,点M是BC边上的中点.
(1)在线段AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,可求得线段AE的长为 .
19.(9分)我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.如图所示,当天舟二号从地面到达点A处时,在P处测得A点的仰角为30°,且A与P两点的距离为6 km,它沿铅垂线上升7.5 s后到达B处,此时在P处测得B点的仰角为45°,求天舟二号从A处上升到B处的平均速度.(结果精确到1 m/s,参考数据:≈1.732,≈1.414)
20.(10分)阅读下面材料.
小军遇到这样一个问题:如图(1),在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=45°,AP=1,求BP的长.
小军的思路是:根据已知条件可以证明△ACP∽△CBP,进一步推理可得BP的长.推理过程如下,请补充完整.
∵AB=AC,∴∠ABC=∠ACB.
∵∠PCB=∠PBA,∴∠PCA= .
∵∠PAC=∠PCB,∴△ACP∽△CBP,
∴==.
∵∠ACB=45°,∴∠BAC=90°,∴= .
∵AP=1,∴PC=.∴PB= .
参考小军的思路,解决问题:
如图(2),在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=30°,求的值.
21.(11分)请根据学习函数的经验,将下列探究函数y=图象与性质的过程补充完整:
(1)函数y=的自变量x的取值范围是 ;
(2)下表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
x … -2 -1 0 n 2 3 4 …
y … - m -1 -2 2 1 …
(3)在如图所示的平面直角坐标系中,描出表中以各组对应值为坐标的点,并画出该函数的图象.
(4)结合函数的图象,写出该函数的一条性质: ;(写出一条即可)
(5)根据图象直接写出>-1时,x的取值范围: .
22.(11分)如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数的图象交AB于点E,连接DE,OD.已知OD=5,tan∠COD=.
(1)求过点D的反比例函数的解析式.
(2)求DE的长.
(3)x轴上是否存在点P使△OPD为直角三角形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
23.(12分)如图(1),矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交边AB(或AD)于点E,PN交边AD(或CD)于点F.当PN旋转至PC处时,∠MPN的旋转随即停止.
(1)特殊情形:如图(2),发现当PM过点A时,PN也恰好过点D,此时△ABP是否与△PCD相似 并说明理由.
(2)类比探究:如图(3),的值是否为定值 若是,请求出该定值;若不是,请说明理由.
(3)拓展延伸:设AE=t,△EPF面积为S,试确定S关于t的函数解析式.
参考答案
一、选择题
1.A
2.C
3.A 由题意,设点A的坐标为(3,4),∴OA=5,∴cos α=,∴这条射线是OA.故选A.
【排雷避坑】本题学生容易选择射线OB,错误的原因是正弦、余弦区分不清楚.在直角三角形中,正弦等于一个锐角的对边与斜边的比,余弦等于一个锐角的邻边与斜边的比.
4.C ∵点D,E是AB边上的三等分点,∴=,=.∵DF∥EG∥BC,∴△ADF∽△AEG,△ADF∽△ABC,∴=()2=,=()2=.令S1=S△ADF=1,则S△AEG=4,S2=3,同理可得S3=S△ABC-S2-S1=5,即S1∶S2∶S3=1∶3∶5.
5.B
【图示速解】易知△DEF∽△ABC,且点F在CP上,∴可得点F的位置如图所示,∴点F的坐标为(4,4),故选B.
6.A 从俯视图可得最底层有5个正方体,由主视图可得上面一层是2个、3个或4个正方体,则该组合体中正方体的个数是7个、8个或9个,所以该组合体中正方体的个数最多是9.
7.D 抛物线y=-x2+3,当y=0时,x=±,当x=0时,y=3,则抛物线y=-x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)为(-1,1),(0,1),(0,2),(1,1),共有4个,即k=4.故D选项符合题意.
8.B 根据题意,得∠CAB=65°-20°=45°,∠ACB=40°+20°=60°,AB=30.过B作BE⊥AC于点E,则∠AEB=∠CEB=90°.在Rt△ABE中,∵∠EAB=45°,AB=30,∴AE=BE=AB=30.在Rt△CBE中,∵∠ACB=60°,∴CE=BE=10,∴AC=AE+CE=30+10,∴A,C两港之间的距离为(30+10)km.故选B.
9.B 如图,过D作DH∥EG交AB于点H,则△AEG∽△ADH,∴=.∵EF⊥AC,∠C=90°,∴EF∥CD,∴△AEF∽△ADC,∴=,∴=.∵EG=EF,∴DH=CD.设DH=x,则CD=x,∵BC=12,∴BD=12-x.∵EF⊥AC,EF⊥EG,DH∥EG,∴EG∥AC∥DH,∴△BDH∽△BCA,∴=,即=,解得x=4,∴CD=4.
10.D ∵点E在线段AB上,∴∠DCE≤∠DCB<90°,故分两种情况讨论.①当∠EDC=90°时,∵AB∥CD,∴∠AED=90°,∴DE=sin A·AD=×10=6,∴AE==8,∴AM=AE=×8=4.②当∠DEC=90°时,过点D作DH⊥AB于点H,过点C作CG⊥AB,交AB的延长线于点G.设AM=x,则AE=2x.易知CG=DH=6,AH=8,HG=CD=16,∴HE=2x-8,EG=16-(2x-8)=24-2x.易证△DHE∽△EGC,∴=,即DH·GC=EG·HE,∴6×6=(24-2x)(2x-8),解得x=8±.当x=8+时,AE=2x=16+2>16,不能满足点E在线段AB上,故舍去,∴AM=8-.综上所述,AM的长为4或8-.
二、填空题
11.球 球无论怎样摆放,它的三视图都是3个全等的圆.
12. 连接BD,DC,由题可得∠DBC=∠DEF,所以tan∠DEF=tan∠DBC==.
13.(4,0) ∵BC∥DE,∴△ABC∽△ADE,∴=.∵BC=1.2,∴DE=2,∴E(4,0).
14.0 ∵直线y=-x与双曲线y=-交于点A(x1,y1),B(x2,y2),∴点A,B关于原点对称,∴x1+x2=0.∵y2=-x2,∴x2=-y2,∴x1-y2=x1+x2=0.
15.-6 ∵cos A=,∴可设OA=a,AB=3a(a>0),∴OB==a.过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F.∵点A在反比例函数y=的图象上,∴可设点A的坐标为(m,),∴OE=m,AE=.∵OA⊥OB,∴易证△AOE∽△OBF,∴=,即=,∴OF=.同理,BF=m,∴点B的坐标为(-,m).把B(-,m)代入y=(k≠0),得k=-6.
三、解答题
16.【参考答案】∵在Rt△ABC中,∠C=90°,AC=3,BC=4,由勾股定理得,
AB===5. (2分)
∴tan B==,sin A==,
cos B==,tan A==, (4分)
∴原式=×+|1-|+
=+1
=. (7分)
17.【解题思路】(1)利用待定系数法即可求解.(2)由反比例函数的性质判断其增减性,再找出临界值,根据题意即可得出V的取值范围.
【参考答案】(1)由题可设p=(k≠0),
将(0.8,120)代入,得120=,
解得k=96,
故所求函数的解析式为p=. (4分)
(2)∵96>0,
∴在第一象限内,p随V的增大而减小.
当p=140 kPa时,V=≈0.69(m3).
故为了安全起见,气体的体积应不小于0.69 m3. (7分)
18.【参考答案】(1)如图,点E即为所求.
(5分)
(2) (8分)
解法提示:∵四边形ABCD是矩形,
∴∠B=90°.
∵点M是BC边上的中点,BC=6,
∴BM=CM=3.
∵AB=4,
∴AM===5.
∵△ADE∽△MAB,
∴=,∴=,
∴AE=.
【破题关键】本题解第(1)问的关键在于分析出∠AED=90°,解第(2)问的关键在于利用相似三角形的性质得到AD∶AM=AE∶BM,属于中考常考题型.
19.【参考答案】由题意可得,∠APD=30°,∠BPD=45°,AP=6 km,∠BDP=90°. (2分)
在Rt△APD中,∵∠APD=30°,AP=6 km,
∴AD=AP=3 km,PD=PA·cos 30°=6×=3(km). (5分)
在Rt△BPD中,
∵∠BPD=45°,PD=3 km,
∴BD=PD·tan 45°=3(km). (7分)
故AB=BD-AD=3-3≈2.196(km)=2 196 m.
2 196÷7.5≈293(m/s).
答:天舟二号从A处上升到B处的平均速度约为293 m/s. (9分)
20.【参考答案】∠PBC 2 (3分)
如图,过点A作AD⊥BC于点D,
∵AB=AC,
∴∠ABC=∠ACB=30°,BD=CD=BC,
∴AD=AC,CD=AD,
∴AC=2AD,BC=2CD=2AD. (6分)
∵∠PCB=∠PBA,
∴∠PCA=∠PBC.
∵∠PAC=∠PCB,
∴△ACP∽△CBP,
∴====. (8分)
设AP=a,则PC=a,
∴PB=3a,
∴=. (10分)
21.【参考答案】(1)x≠1 (2分)
解法提示:∵x-1≠0,∴x≠1.
(2)- (4分)
解法提示:当x=-1时,y===-;
当y=2时,2=,解得x=.
(3)描点、连线如图所示.
(7分)
(4)由图象可得,当x>1时,y随x的增大而减小[或函数图象关于(1,0)成中心对称,答案不唯一] (9分)
(5)x<0或x>1 (11分)
22.【解题思路】(1)设OC=3x,则CD=4x.在Rt△OCD中,根据勾股定理及OD的长可求得OC,CD的长,从而可得点D的坐标,然后利用待定系数法求解即可.(2)易得AB的长及点E的坐标,从而可得BE的长.在Rt△BDE中,根据勾股定理即可得DE的长.(3)分∠OPD=90°和∠ODP=90°两种情况讨论.
【参考答案】(1)∵四边形OABC是矩形,
∴∠OCD=90°.
由tan∠COD==,
可设OC=3x,则CD=4x.
在Rt△OCD中,根据勾股定理,得
OD==5x.
又OD=5,∴x=1,
∴OC=3,CD=4,
∴点D(4,3). (3分)
设过点D的反比例函数的解析式为y=(k≠0),
将点D的坐标代入,得3=,∴k=12,
∴过点D的反比例函数的解析式为y=. (4分)
(2)∵点D是BC的中点,四边形OABC是矩形,
∴BC=2CD=8,AB=OC=3,
∴点E的横坐标为8.
∵点E在反比例函数y=的图象上,
∴点E(8,), (6分)
∴BE=AB-AE=3-=.
在Rt△BDE中,根据勾股定理,得
DE===. (8分)
(3)存在. (9分)
满足题意的点P的坐标为(4,0)或(,0). (11分)
解法提示:分两种情况.
①当∠OPD=90°时,PD⊥x轴,
∴OP=CD=4,
∴点P(4,0).
②当∠ODP=90°时,
如图,过点D作DH⊥x轴于点H,则OH=CD=4.
易得△ODH∽△OPD,
∴=,
∴OP==,
∴点P(,0).
综上,满足题意的点P的坐标为(4,0)或(,0).
23.【解题思路】(1)根据矩形的性质可知∠B=∠C=90°,再通过角的计算得出∠BAP=∠CPD,由此即可得出△ABP∽△PCD.(2)过点F作FH⊥PC于点H,根据矩形的性质以及角的计算找出∠B=∠FHP=90°,∠BEP=∠HPF,由此即可得出△BEP∽△HPF,根据相似三角形的性质,找出边与边之间的关系即可得出结论.(3)分点E在AB和AD上两种情况考虑,根据相似三角形的性质找出各边的长度,再利用分割图形求面积法找出S与t之间的函数关系式,进而求出当△EPF的面积为4.2时,对应的t的值.
【参考答案】(1)∵四边形ABCD为矩形,
∴∠B=∠C=90°,∠BAP+∠BPA=90°.
∵∠MPN=90°,
∴∠BPA+∠CPD=90°,
∴∠BAP=∠CPD,
∴△ABP∽△PCD. (2分)
(2)是定值. (3分)
如图(1),过点F作FH⊥PC于点H. (4分)
∵矩形ABCD中,AB=2,
∴∠B=∠FHP=90°,HF=AB=2,
∴∠BPE+∠BEP=90°.
∵∠MPN=90°,
∴∠BPE+∠HPF=90°,
∴∠BEP=∠HPF,
∴△BEP∽△HPF,
∴= .
∵BP=1,
∴=. (6分)
(3)分两种情况:
①如图(1),当点E在AB上时,0≤t≤2.
∵AE=t,AB=2,
∴BE=2-t.
由(2)可知△BEP∽△HPF,
∴=,即=,
∴HP=4-2t.
∵AF=BH=PB+PH=5-2t,
∴S=S矩形ABHF-S△AEF-S△BEP-S△PHF=AB·AF-AE·AF-BE·PB-PH·FH=t2-4t+5(0≤t≤2). (9分)
②如图(2),当点E在AD上时,0≤t≤1,过点E作EK⊥BP于点K,
∵AE=t,BP=1,
∴PK=1-t.
由(2)同理可证△PKE∽△FCP,
∴=,即=,
∴FC=2-2t,
∴DF=CD-FC=2t,DE=AD-AE=5-t,
∴S=S矩形EKCD-S△EKP-S△EDF-S△PCF=CD·DE-EK·KP-DE·DF-PC·FC=t2-2t+5(0≤t≤1). (12分)
图(1) 图(2)
时间:90分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.下列选项中的点在反比例函数y=图象上的是( )
A.(2,3) B.(4,2) C.(-6,1) D.(-2,3)
2.下列四幅图,表示两棵树在同一时刻阳光下的影子的是( )
A B C D
3.如图,在平面直角坐标系中,从原点O引一条射线,设这条射线与x轴的正半轴的夹角为α,若cos α=,则这条射线是( )
A.OA B.OB C.OC D.OD
(第3题) (第4题)
4.如图,已知点D,E是AB边上的三等分点,线段DF,EG将△ABC分成三部分,且DF∥EG∥BC,图中三部分的面积分别为S1,S2,S3,则S1∶S2∶S3=( )
A.1∶2∶3 B.1∶2∶4 C.1∶3∶5 D.2∶3∶4
5.如图,在平面直角坐标系中,以P(4,6)为位似中心,把△ABC缩小得到△DEF,若变换后,点A,B的对应点分别为点D,E,则点C的对应点F的坐标应为( )
A.(4,2) B.(4,4) C.(4,5) D.(5,4)
6.已知一个组合体是由几个相同的正方体叠合在一起组成的,该组合体的主视图与俯视图如图所示,则该组合体中正方体的个数最多是( )
A.9 B.10 C.8 D.7
7.如图,若抛物线y=-x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k,则反比例函数y=(x>0)的图象是( )
A B C D
8.如图,一艘船由A港沿北偏东65°方向航行30 km至B港,再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向上,则A,C两港之间的距离为( )
A.(30+30)km B.(30+10)km
C.(10+30)km D.30 km
9.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( )
A.3.6 B.4 C.4.8 D.5
10.如图,已知 ABCD中,AB=16,AD=10,sin A=,点M为AB边上一动点,过点M作MN⊥AB交AD边于点N,作点A关于直线MN的对称点E,且点E落在线段AB上,连接DE,CE.当△CDE为直角三角形时,AM的长为( )
A.4 B.8+或8-
C.4或8+ D.4或8-
二、填空题(共5小题,每小题3分,共15分)
11.请写出一个任意摆放后三视图都相同的几何体: .
12.如图,边长为1的小正方形网格中,点A,B,C,D,E均在格点上,半径为2的☉A与BC交于点F,则tan∠DEF= .
(第12题) (第13题)
13.小明家的客厅有一张直径为1.2米,高0.8米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE.建立如图所示的平面直角坐标系,其中点D的坐标为(2,0),则点E的坐标是 .
14.在平面直角坐标系中,直线y=-x与双曲线y=-交于点A(x1,y1),B(x2,y2),则x1-y2的值为 .
15.如图,已知第一象限内的点A在反比例函数y=的图象上,第二象限内的点B在反比例函数y=(k≠0)的图象上,且OA⊥OB,cos A=,则k的值为 .
三、解答题(共8小题,共75分)
16.(7分)如图,已知在Rt△ABC中,∠C=90°,AC=3,BC=4.求tan Bsin A+|1-cos B|+的值.
17.(7分)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该函数的解析式;
(2)当气球内的气压大于140 kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少 (精确到0.01 m3)
18.(8分)如图,在矩形ABCD中,AB=4,BC=6,点M是BC边上的中点.
(1)在线段AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,可求得线段AE的长为 .
19.(9分)我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.如图所示,当天舟二号从地面到达点A处时,在P处测得A点的仰角为30°,且A与P两点的距离为6 km,它沿铅垂线上升7.5 s后到达B处,此时在P处测得B点的仰角为45°,求天舟二号从A处上升到B处的平均速度.(结果精确到1 m/s,参考数据:≈1.732,≈1.414)
20.(10分)阅读下面材料.
小军遇到这样一个问题:如图(1),在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=45°,AP=1,求BP的长.
小军的思路是:根据已知条件可以证明△ACP∽△CBP,进一步推理可得BP的长.推理过程如下,请补充完整.
∵AB=AC,∴∠ABC=∠ACB.
∵∠PCB=∠PBA,∴∠PCA= .
∵∠PAC=∠PCB,∴△ACP∽△CBP,
∴==.
∵∠ACB=45°,∴∠BAC=90°,∴= .
∵AP=1,∴PC=.∴PB= .
参考小军的思路,解决问题:
如图(2),在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=30°,求的值.
21.(11分)请根据学习函数的经验,将下列探究函数y=图象与性质的过程补充完整:
(1)函数y=的自变量x的取值范围是 ;
(2)下表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
x … -2 -1 0 n 2 3 4 …
y … - m -1 -2 2 1 …
(3)在如图所示的平面直角坐标系中,描出表中以各组对应值为坐标的点,并画出该函数的图象.
(4)结合函数的图象,写出该函数的一条性质: ;(写出一条即可)
(5)根据图象直接写出>-1时,x的取值范围: .
22.(11分)如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数的图象交AB于点E,连接DE,OD.已知OD=5,tan∠COD=.
(1)求过点D的反比例函数的解析式.
(2)求DE的长.
(3)x轴上是否存在点P使△OPD为直角三角形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
23.(12分)如图(1),矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交边AB(或AD)于点E,PN交边AD(或CD)于点F.当PN旋转至PC处时,∠MPN的旋转随即停止.
(1)特殊情形:如图(2),发现当PM过点A时,PN也恰好过点D,此时△ABP是否与△PCD相似 并说明理由.
(2)类比探究:如图(3),的值是否为定值 若是,请求出该定值;若不是,请说明理由.
(3)拓展延伸:设AE=t,△EPF面积为S,试确定S关于t的函数解析式.
参考答案
一、选择题
1.A
2.C
3.A 由题意,设点A的坐标为(3,4),∴OA=5,∴cos α=,∴这条射线是OA.故选A.
【排雷避坑】本题学生容易选择射线OB,错误的原因是正弦、余弦区分不清楚.在直角三角形中,正弦等于一个锐角的对边与斜边的比,余弦等于一个锐角的邻边与斜边的比.
4.C ∵点D,E是AB边上的三等分点,∴=,=.∵DF∥EG∥BC,∴△ADF∽△AEG,△ADF∽△ABC,∴=()2=,=()2=.令S1=S△ADF=1,则S△AEG=4,S2=3,同理可得S3=S△ABC-S2-S1=5,即S1∶S2∶S3=1∶3∶5.
5.B
【图示速解】易知△DEF∽△ABC,且点F在CP上,∴可得点F的位置如图所示,∴点F的坐标为(4,4),故选B.
6.A 从俯视图可得最底层有5个正方体,由主视图可得上面一层是2个、3个或4个正方体,则该组合体中正方体的个数是7个、8个或9个,所以该组合体中正方体的个数最多是9.
7.D 抛物线y=-x2+3,当y=0时,x=±,当x=0时,y=3,则抛物线y=-x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)为(-1,1),(0,1),(0,2),(1,1),共有4个,即k=4.故D选项符合题意.
8.B 根据题意,得∠CAB=65°-20°=45°,∠ACB=40°+20°=60°,AB=30.过B作BE⊥AC于点E,则∠AEB=∠CEB=90°.在Rt△ABE中,∵∠EAB=45°,AB=30,∴AE=BE=AB=30.在Rt△CBE中,∵∠ACB=60°,∴CE=BE=10,∴AC=AE+CE=30+10,∴A,C两港之间的距离为(30+10)km.故选B.
9.B 如图,过D作DH∥EG交AB于点H,则△AEG∽△ADH,∴=.∵EF⊥AC,∠C=90°,∴EF∥CD,∴△AEF∽△ADC,∴=,∴=.∵EG=EF,∴DH=CD.设DH=x,则CD=x,∵BC=12,∴BD=12-x.∵EF⊥AC,EF⊥EG,DH∥EG,∴EG∥AC∥DH,∴△BDH∽△BCA,∴=,即=,解得x=4,∴CD=4.
10.D ∵点E在线段AB上,∴∠DCE≤∠DCB<90°,故分两种情况讨论.①当∠EDC=90°时,∵AB∥CD,∴∠AED=90°,∴DE=sin A·AD=×10=6,∴AE==8,∴AM=AE=×8=4.②当∠DEC=90°时,过点D作DH⊥AB于点H,过点C作CG⊥AB,交AB的延长线于点G.设AM=x,则AE=2x.易知CG=DH=6,AH=8,HG=CD=16,∴HE=2x-8,EG=16-(2x-8)=24-2x.易证△DHE∽△EGC,∴=,即DH·GC=EG·HE,∴6×6=(24-2x)(2x-8),解得x=8±.当x=8+时,AE=2x=16+2>16,不能满足点E在线段AB上,故舍去,∴AM=8-.综上所述,AM的长为4或8-.
二、填空题
11.球 球无论怎样摆放,它的三视图都是3个全等的圆.
12. 连接BD,DC,由题可得∠DBC=∠DEF,所以tan∠DEF=tan∠DBC==.
13.(4,0) ∵BC∥DE,∴△ABC∽△ADE,∴=.∵BC=1.2,∴DE=2,∴E(4,0).
14.0 ∵直线y=-x与双曲线y=-交于点A(x1,y1),B(x2,y2),∴点A,B关于原点对称,∴x1+x2=0.∵y2=-x2,∴x2=-y2,∴x1-y2=x1+x2=0.
15.-6 ∵cos A=,∴可设OA=a,AB=3a(a>0),∴OB==a.过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F.∵点A在反比例函数y=的图象上,∴可设点A的坐标为(m,),∴OE=m,AE=.∵OA⊥OB,∴易证△AOE∽△OBF,∴=,即=,∴OF=.同理,BF=m,∴点B的坐标为(-,m).把B(-,m)代入y=(k≠0),得k=-6.
三、解答题
16.【参考答案】∵在Rt△ABC中,∠C=90°,AC=3,BC=4,由勾股定理得,
AB===5. (2分)
∴tan B==,sin A==,
cos B==,tan A==, (4分)
∴原式=×+|1-|+
=+1
=. (7分)
17.【解题思路】(1)利用待定系数法即可求解.(2)由反比例函数的性质判断其增减性,再找出临界值,根据题意即可得出V的取值范围.
【参考答案】(1)由题可设p=(k≠0),
将(0.8,120)代入,得120=,
解得k=96,
故所求函数的解析式为p=. (4分)
(2)∵96>0,
∴在第一象限内,p随V的增大而减小.
当p=140 kPa时,V=≈0.69(m3).
故为了安全起见,气体的体积应不小于0.69 m3. (7分)
18.【参考答案】(1)如图,点E即为所求.
(5分)
(2) (8分)
解法提示:∵四边形ABCD是矩形,
∴∠B=90°.
∵点M是BC边上的中点,BC=6,
∴BM=CM=3.
∵AB=4,
∴AM===5.
∵△ADE∽△MAB,
∴=,∴=,
∴AE=.
【破题关键】本题解第(1)问的关键在于分析出∠AED=90°,解第(2)问的关键在于利用相似三角形的性质得到AD∶AM=AE∶BM,属于中考常考题型.
19.【参考答案】由题意可得,∠APD=30°,∠BPD=45°,AP=6 km,∠BDP=90°. (2分)
在Rt△APD中,∵∠APD=30°,AP=6 km,
∴AD=AP=3 km,PD=PA·cos 30°=6×=3(km). (5分)
在Rt△BPD中,
∵∠BPD=45°,PD=3 km,
∴BD=PD·tan 45°=3(km). (7分)
故AB=BD-AD=3-3≈2.196(km)=2 196 m.
2 196÷7.5≈293(m/s).
答:天舟二号从A处上升到B处的平均速度约为293 m/s. (9分)
20.【参考答案】∠PBC 2 (3分)
如图,过点A作AD⊥BC于点D,
∵AB=AC,
∴∠ABC=∠ACB=30°,BD=CD=BC,
∴AD=AC,CD=AD,
∴AC=2AD,BC=2CD=2AD. (6分)
∵∠PCB=∠PBA,
∴∠PCA=∠PBC.
∵∠PAC=∠PCB,
∴△ACP∽△CBP,
∴====. (8分)
设AP=a,则PC=a,
∴PB=3a,
∴=. (10分)
21.【参考答案】(1)x≠1 (2分)
解法提示:∵x-1≠0,∴x≠1.
(2)- (4分)
解法提示:当x=-1时,y===-;
当y=2时,2=,解得x=.
(3)描点、连线如图所示.
(7分)
(4)由图象可得,当x>1时,y随x的增大而减小[或函数图象关于(1,0)成中心对称,答案不唯一] (9分)
(5)x<0或x>1 (11分)
22.【解题思路】(1)设OC=3x,则CD=4x.在Rt△OCD中,根据勾股定理及OD的长可求得OC,CD的长,从而可得点D的坐标,然后利用待定系数法求解即可.(2)易得AB的长及点E的坐标,从而可得BE的长.在Rt△BDE中,根据勾股定理即可得DE的长.(3)分∠OPD=90°和∠ODP=90°两种情况讨论.
【参考答案】(1)∵四边形OABC是矩形,
∴∠OCD=90°.
由tan∠COD==,
可设OC=3x,则CD=4x.
在Rt△OCD中,根据勾股定理,得
OD==5x.
又OD=5,∴x=1,
∴OC=3,CD=4,
∴点D(4,3). (3分)
设过点D的反比例函数的解析式为y=(k≠0),
将点D的坐标代入,得3=,∴k=12,
∴过点D的反比例函数的解析式为y=. (4分)
(2)∵点D是BC的中点,四边形OABC是矩形,
∴BC=2CD=8,AB=OC=3,
∴点E的横坐标为8.
∵点E在反比例函数y=的图象上,
∴点E(8,), (6分)
∴BE=AB-AE=3-=.
在Rt△BDE中,根据勾股定理,得
DE===. (8分)
(3)存在. (9分)
满足题意的点P的坐标为(4,0)或(,0). (11分)
解法提示:分两种情况.
①当∠OPD=90°时,PD⊥x轴,
∴OP=CD=4,
∴点P(4,0).
②当∠ODP=90°时,
如图,过点D作DH⊥x轴于点H,则OH=CD=4.
易得△ODH∽△OPD,
∴=,
∴OP==,
∴点P(,0).
综上,满足题意的点P的坐标为(4,0)或(,0).
23.【解题思路】(1)根据矩形的性质可知∠B=∠C=90°,再通过角的计算得出∠BAP=∠CPD,由此即可得出△ABP∽△PCD.(2)过点F作FH⊥PC于点H,根据矩形的性质以及角的计算找出∠B=∠FHP=90°,∠BEP=∠HPF,由此即可得出△BEP∽△HPF,根据相似三角形的性质,找出边与边之间的关系即可得出结论.(3)分点E在AB和AD上两种情况考虑,根据相似三角形的性质找出各边的长度,再利用分割图形求面积法找出S与t之间的函数关系式,进而求出当△EPF的面积为4.2时,对应的t的值.
【参考答案】(1)∵四边形ABCD为矩形,
∴∠B=∠C=90°,∠BAP+∠BPA=90°.
∵∠MPN=90°,
∴∠BPA+∠CPD=90°,
∴∠BAP=∠CPD,
∴△ABP∽△PCD. (2分)
(2)是定值. (3分)
如图(1),过点F作FH⊥PC于点H. (4分)
∵矩形ABCD中,AB=2,
∴∠B=∠FHP=90°,HF=AB=2,
∴∠BPE+∠BEP=90°.
∵∠MPN=90°,
∴∠BPE+∠HPF=90°,
∴∠BEP=∠HPF,
∴△BEP∽△HPF,
∴= .
∵BP=1,
∴=. (6分)
(3)分两种情况:
①如图(1),当点E在AB上时,0≤t≤2.
∵AE=t,AB=2,
∴BE=2-t.
由(2)可知△BEP∽△HPF,
∴=,即=,
∴HP=4-2t.
∵AF=BH=PB+PH=5-2t,
∴S=S矩形ABHF-S△AEF-S△BEP-S△PHF=AB·AF-AE·AF-BE·PB-PH·FH=t2-4t+5(0≤t≤2). (9分)
②如图(2),当点E在AD上时,0≤t≤1,过点E作EK⊥BP于点K,
∵AE=t,BP=1,
∴PK=1-t.
由(2)同理可证△PKE∽△FCP,
∴=,即=,
∴FC=2-2t,
∴DF=CD-FC=2t,DE=AD-AE=5-t,
∴S=S矩形EKCD-S△EKP-S△EDF-S△PCF=CD·DE-EK·KP-DE·DF-PC·FC=t2-2t+5(0≤t≤1). (12分)
图(1) 图(2)
同课章节目录
