2022-2023学年人教版 八年级下册数学第十七章勾股定理同步练习 (无答案)
文档属性
| 名称 | 2022-2023学年人教版 八年级下册数学第十七章勾股定理同步练习 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 116.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 13:05:46 | ||
图片预览

文档简介
人教版八年级下册数学第十七章勾股定理
姓名: 得分: 日期:
一、选择题(本大题共 14 小题)
1、已知 中, ,若a+b=14cm,c=10cm,则 的面积是( )
A. B. C. D.
2、在 中, ,AC=3,BC=4,则AB=( )
A. 3 B. 4 C. 5 D. 6
3、如图在 中, 平分∠BAC,DE⊥AB于E,DE=3,BD=2CD,则
A. 7 B. 8 C. 9 D. 10
4、判断下列三条线段a,b,c组成的三角形不是直角三角形的是( )
A.a=4,b=5,c=3 B.a=7,b=25,c=24 C.a=40,b=50,c=60 D.a=5,b=12,c=13
5、如图,以两个半圆的直径作为直角边,正方形的一边作为斜边构成一个直角三角形,已知半圆面积分别为π和3π,则正方形的面积为( )
A. 16π B. 32π C. 16 D. 32
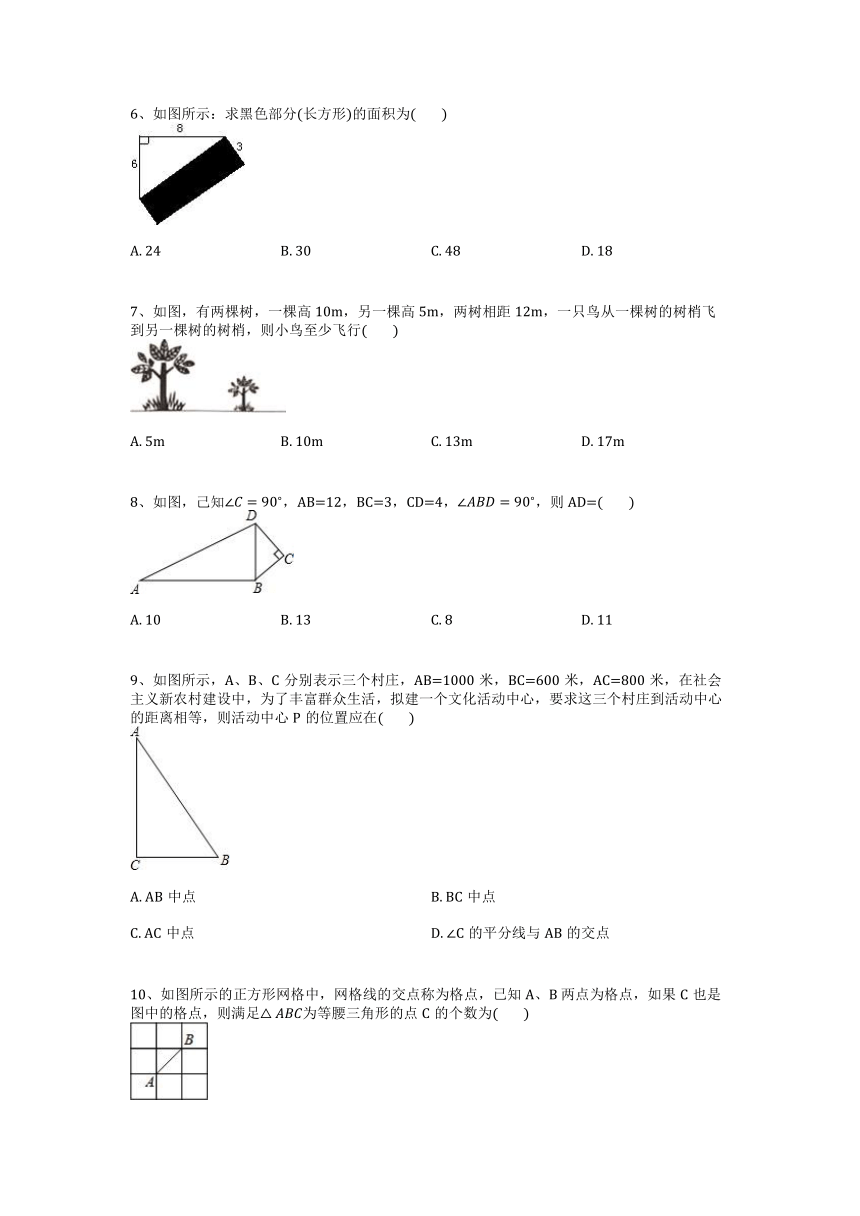
6、如图所示:求黑色部分(长方形)的面积为( )
A. 24 B. 30 C. 48 D. 18
7、如图,有两棵树,一棵高10m,另一棵高5m,两树相距12m,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A. 5m B. 10m C. 13m D. 17m
8、如图,己知 ,AB=12,BC=3,CD=4, ,则AD=( )
A. 10 B. 13 C. 8 D. 11
9、如图所示,A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A. AB中点 B. BC中点
C. AC中点 D. ∠C的平分线与AB的交点
10、如图所示的正方形网格中,网格线的交点称为格点,已知A、B 两点为格点,如果C也是图中的格点,则满足 为等腰三角形的点C的个数为( )
A. 6个 B. 7个 C. 8个 D. 9个
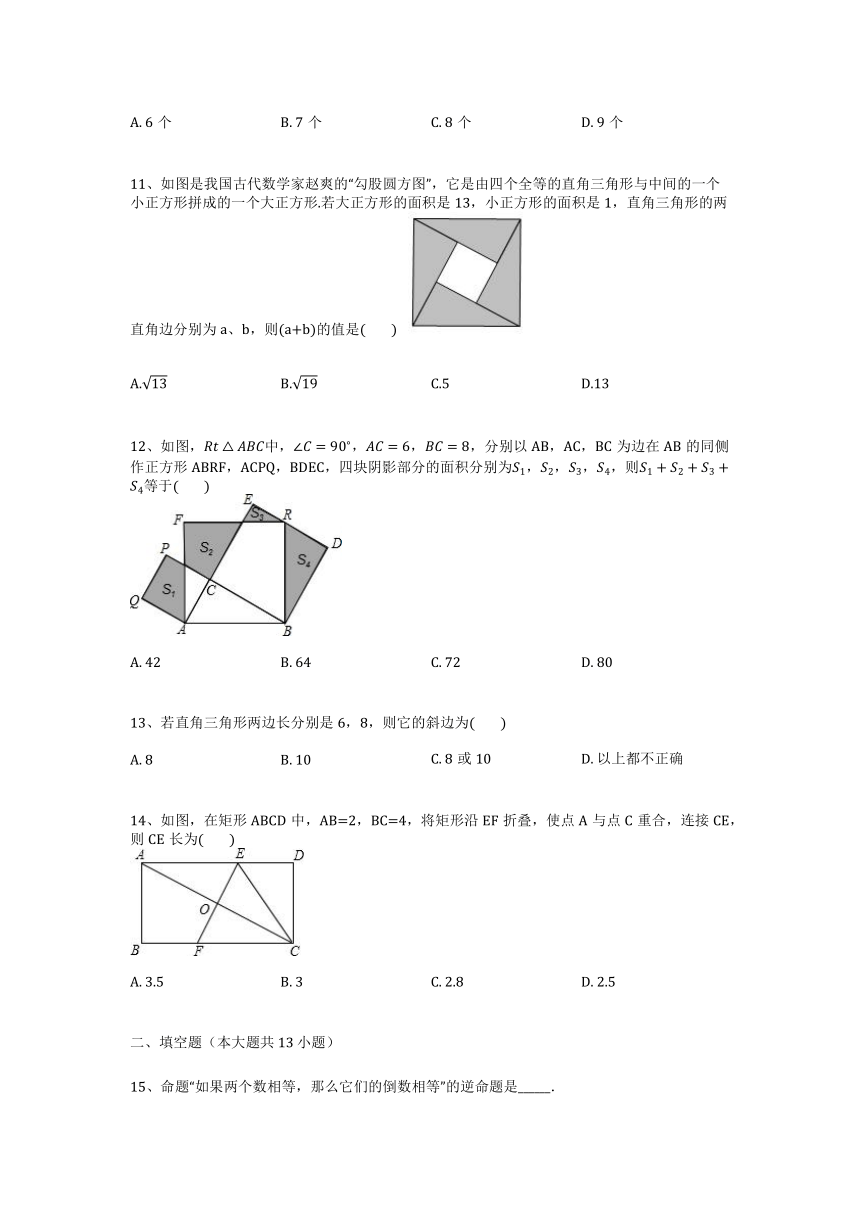
11、如图是我国古代数学家赵爽的“勾股圆方图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a、b,则(a+b)的值是( )
A. B. C.5 D.13
12、如图, 中, ,分别以AB,AC,BC为边在AB的同侧作正方形ABRF,ACPQ,BDEC,四块阴影部分的面积分别为 ,则 等于( )
A. 42 B. 64 C. 72 D. 80
13、若直角三角形两边长分别是6,8,则它的斜边为( )
A. 8 B. 10 C. 8或10 D. 以上都不正确
14、如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )
A. 3.5 B. 3 C. 2.8 D. 2.5
二、填空题(本大题共 13 小题)
15、命题“如果两个数相等,那么它们的倒数相等”的逆命题是______.
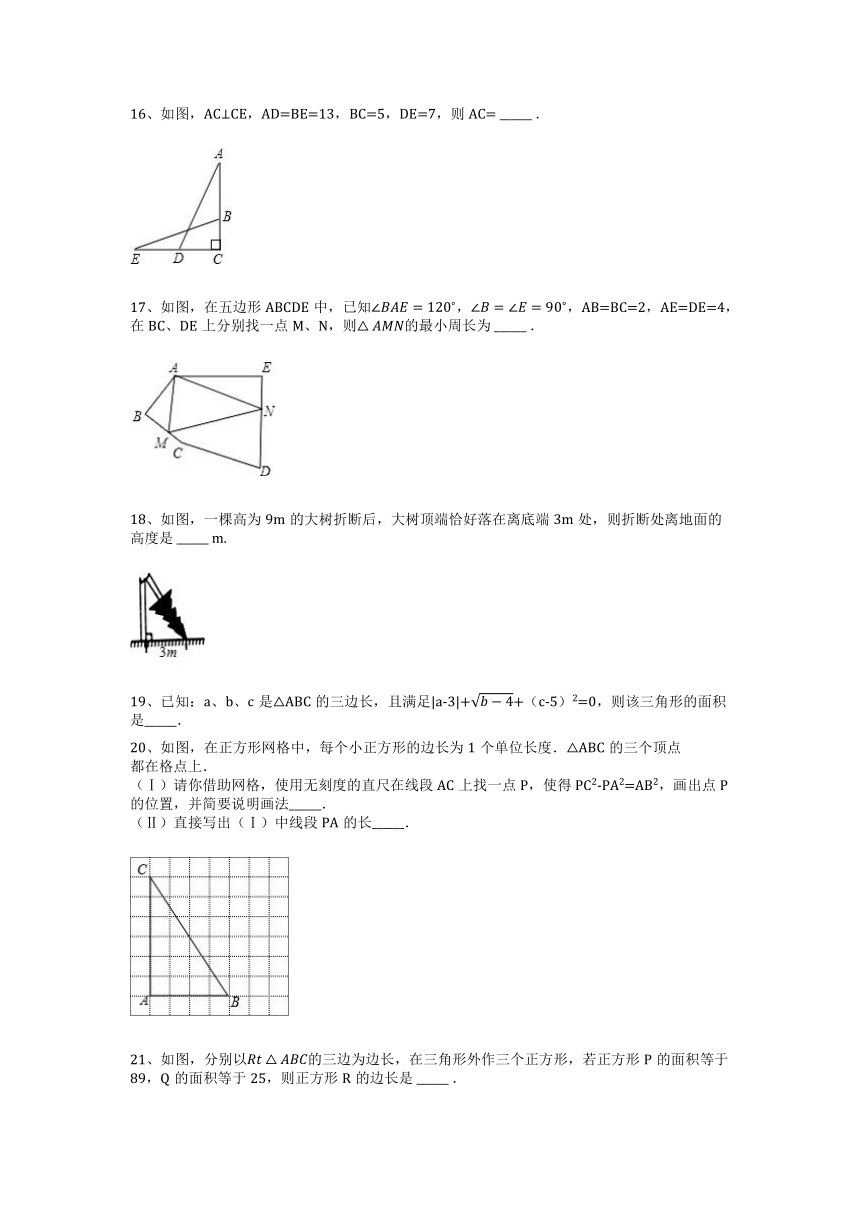
16、如图,AC⊥CE,AD=BE=13,BC=5,DE=7,则AC= ______ .
17、如图,在五边形ABCDE中,已知 , ,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,则 的最小周长为 ______ .
18、如图,一棵高为9m的大树折断后,大树顶端恰好落在离底端3m处,则折断处离地面的高度是 ______ m.
19、已知:a、b、c是△ABC的三边长,且满足|a-3|+ +(c-5)2=0,则该三角形的面积是______.
20、如图,在正方形网格中,每个小正方形的边长为1个单位长度.△ABC的三个顶点
都在格点上.
(Ⅰ)请你借助网格,使用无刻度的直尺在线段AC上找一点P,使得PC2-PA2=AB2,画出点P的位置,并简要说明画法______.
(Ⅱ)直接写出(Ⅰ)中线段PA的长______.
21、如图,分别以 的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是 ______ .
22、如图,正方形内数字分别为所在正方形的面积,则图中字母A,B,C所代表的正方形面积是 ______ .
23、如图,在 中,AB=AC=10,BC=12,若点P在边AC上移动,则BP的最小值是 ______ .
24、如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要 ______ 元钱.
25、边长为7,24,25的 内有一点P到三边距离相等,则这个距离为 ______ .
26、一个圆筒底面直径为10cm,高24cm,则桶内所能容下的最长木棒为 ______ .
27、如图,在 中, 为BC上一点,过点D作DE⊥AB,垂足为E,连接AD,若CD=DE=1,则AB的长为 ______ .
三、解答题(本大题共 6 小题)
28、如图,已知A(-2,3)、B(4,3).C(-1,-3)
(1)点B到坐标原点的距离为______;
(2)求BC的长;
(3)点P在y轴上,当△ABP的面积为3时,请直接写出点P的坐标.
29、如图,边长为1的正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的
三角形叫做格点三角形.
(1)请在正方形网格中画出格点△ABC,使AB= ,BC= ,AC= ;
(2)求AC边上的高.
30、如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,求AC的长.
31、如图,正方形网格中每个小方格的边长为1,且点A,B,C均为格点.
(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)求△ABC的面积;
(3)边AB=______(不用写过程);
(4)在直线l上找一点D,使AD+BD最小.
32、如图,在四边形ABCD中,∠B=∠C=90°,点E在BC上,AB=BE=1,ED=2 ,AD= .
(1)求∠BED的度数;
(2)直接写出四边形ABCD的面积为______.
33、如图,在△ABC中,AC=BC,∠C=90°,AD是∠CAB的角平分线,DE⊥AB,垂足为E.
(1)已知CD= ,求AC的长.
(2)求证:AB=AC+CD.
姓名: 得分: 日期:
一、选择题(本大题共 14 小题)
1、已知 中, ,若a+b=14cm,c=10cm,则 的面积是( )
A. B. C. D.
2、在 中, ,AC=3,BC=4,则AB=( )
A. 3 B. 4 C. 5 D. 6
3、如图在 中, 平分∠BAC,DE⊥AB于E,DE=3,BD=2CD,则
A. 7 B. 8 C. 9 D. 10
4、判断下列三条线段a,b,c组成的三角形不是直角三角形的是( )
A.a=4,b=5,c=3 B.a=7,b=25,c=24 C.a=40,b=50,c=60 D.a=5,b=12,c=13
5、如图,以两个半圆的直径作为直角边,正方形的一边作为斜边构成一个直角三角形,已知半圆面积分别为π和3π,则正方形的面积为( )
A. 16π B. 32π C. 16 D. 32
6、如图所示:求黑色部分(长方形)的面积为( )
A. 24 B. 30 C. 48 D. 18
7、如图,有两棵树,一棵高10m,另一棵高5m,两树相距12m,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A. 5m B. 10m C. 13m D. 17m
8、如图,己知 ,AB=12,BC=3,CD=4, ,则AD=( )
A. 10 B. 13 C. 8 D. 11
9、如图所示,A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A. AB中点 B. BC中点
C. AC中点 D. ∠C的平分线与AB的交点
10、如图所示的正方形网格中,网格线的交点称为格点,已知A、B 两点为格点,如果C也是图中的格点,则满足 为等腰三角形的点C的个数为( )
A. 6个 B. 7个 C. 8个 D. 9个
11、如图是我国古代数学家赵爽的“勾股圆方图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a、b,则(a+b)的值是( )
A. B. C.5 D.13
12、如图, 中, ,分别以AB,AC,BC为边在AB的同侧作正方形ABRF,ACPQ,BDEC,四块阴影部分的面积分别为 ,则 等于( )
A. 42 B. 64 C. 72 D. 80
13、若直角三角形两边长分别是6,8,则它的斜边为( )
A. 8 B. 10 C. 8或10 D. 以上都不正确
14、如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )
A. 3.5 B. 3 C. 2.8 D. 2.5
二、填空题(本大题共 13 小题)
15、命题“如果两个数相等,那么它们的倒数相等”的逆命题是______.
16、如图,AC⊥CE,AD=BE=13,BC=5,DE=7,则AC= ______ .
17、如图,在五边形ABCDE中,已知 , ,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,则 的最小周长为 ______ .
18、如图,一棵高为9m的大树折断后,大树顶端恰好落在离底端3m处,则折断处离地面的高度是 ______ m.
19、已知:a、b、c是△ABC的三边长,且满足|a-3|+ +(c-5)2=0,则该三角形的面积是______.
20、如图,在正方形网格中,每个小正方形的边长为1个单位长度.△ABC的三个顶点
都在格点上.
(Ⅰ)请你借助网格,使用无刻度的直尺在线段AC上找一点P,使得PC2-PA2=AB2,画出点P的位置,并简要说明画法______.
(Ⅱ)直接写出(Ⅰ)中线段PA的长______.
21、如图,分别以 的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是 ______ .
22、如图,正方形内数字分别为所在正方形的面积,则图中字母A,B,C所代表的正方形面积是 ______ .
23、如图,在 中,AB=AC=10,BC=12,若点P在边AC上移动,则BP的最小值是 ______ .
24、如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要 ______ 元钱.
25、边长为7,24,25的 内有一点P到三边距离相等,则这个距离为 ______ .
26、一个圆筒底面直径为10cm,高24cm,则桶内所能容下的最长木棒为 ______ .
27、如图,在 中, 为BC上一点,过点D作DE⊥AB,垂足为E,连接AD,若CD=DE=1,则AB的长为 ______ .
三、解答题(本大题共 6 小题)
28、如图,已知A(-2,3)、B(4,3).C(-1,-3)
(1)点B到坐标原点的距离为______;
(2)求BC的长;
(3)点P在y轴上,当△ABP的面积为3时,请直接写出点P的坐标.
29、如图,边长为1的正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的
三角形叫做格点三角形.
(1)请在正方形网格中画出格点△ABC,使AB= ,BC= ,AC= ;
(2)求AC边上的高.
30、如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,求AC的长.
31、如图,正方形网格中每个小方格的边长为1,且点A,B,C均为格点.
(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)求△ABC的面积;
(3)边AB=______(不用写过程);
(4)在直线l上找一点D,使AD+BD最小.
32、如图,在四边形ABCD中,∠B=∠C=90°,点E在BC上,AB=BE=1,ED=2 ,AD= .
(1)求∠BED的度数;
(2)直接写出四边形ABCD的面积为______.
33、如图,在△ABC中,AC=BC,∠C=90°,AD是∠CAB的角平分线,DE⊥AB,垂足为E.
(1)已知CD= ,求AC的长.
(2)求证:AB=AC+CD.
