沪教版(五四学制)七年级下册14.5等腰三角形的性质 课件(共24张PPT)
文档属性
| 名称 | 沪教版(五四学制)七年级下册14.5等腰三角形的性质 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 676.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
2022-2023学年七年级数学下册同步精品课堂(沪教版)
14.5等腰三角形的性质
第 14章 三角形
3、在你们的印象里,什么样的三角形叫做等腰三角形?
有两条边相等的三角形叫做等腰三角形
2、上面三个三角形按边分类是什么样的三角形
1、上面三个三角形按角分类是什么样的三角形
复习回顾:
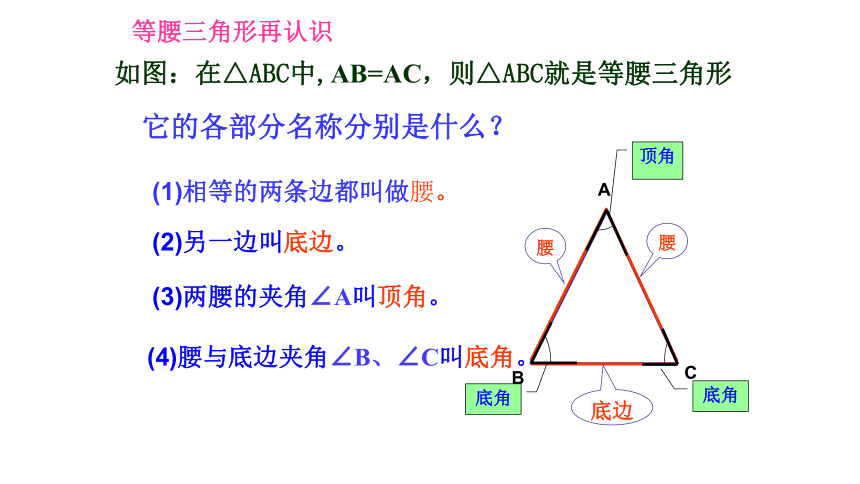
如图:在△ABC中,AB=AC,则△ABC就是等腰三角形
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边都叫做腰。
腰
腰
底边
(2)另一边叫底边。
顶角
底角
底角
(3)两腰的夹角∠A叫顶角。
(4)腰与底边夹角∠B、∠C叫底角。
等腰三角形再认识
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC,
说明∠B= C的理由.
猜想
A
B
C
D
问题
等腰三角形的两个底角具有怎样的大小关系
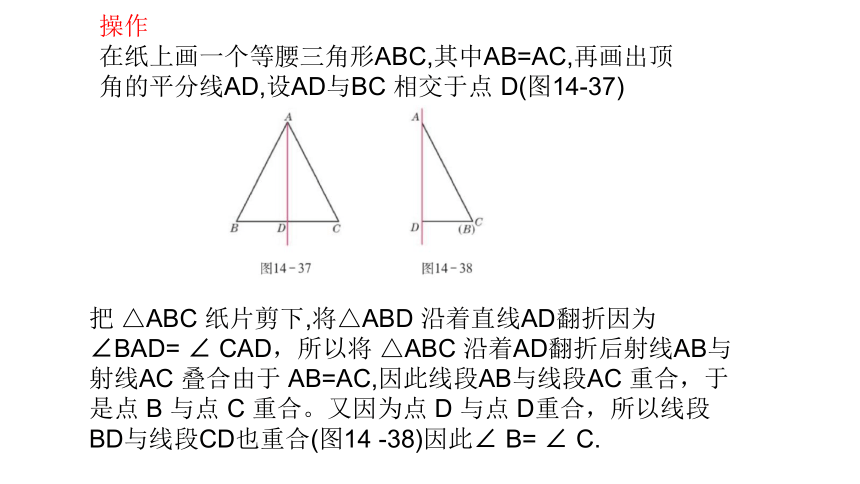
操作
在纸上画一个等腰三角形ABC,其中AB=AC,再画出顶角的平分线AD,设AD与BC 相交于点 D(图14-37)
把 △ABC 纸片剪下,将△ABD 沿着直线AD翻折因为∠BAD= ∠ CAD,所以将 △ABC 沿着AD翻折后射线AB与射线AC 叠合由于 AB=AC,因此线段AB与线段AC 重合,于是点 B 与点 C 重合。又因为点 D 与点 D重合,所以线段BD与线段CD也重合(图14 -38)因此∠ B= ∠ C.
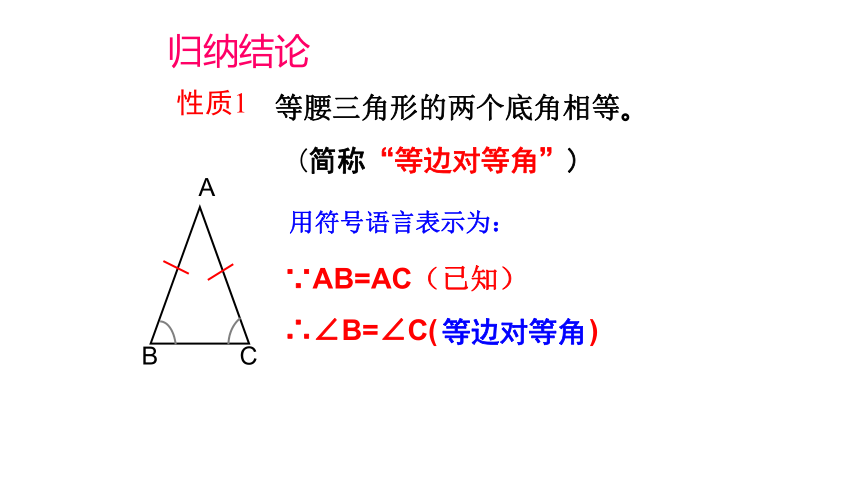
归纳结论
等腰三角形的两个底角相等。
性质1
(简称“等边对等角”)
用符号语言表示为:
A
B
C
∵AB=AC(已知)
∴∠B=∠C( )
等边对等角
A
B
C
则有∠1= ∠2(角平分线的意义)
D
1
2
在△ABD和△ACD中
证明: 过点A作∠BAC的角平分
线AD,交BC于点D.
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
我们可以直接利用全等三角形对等腰三角形的性质进行说理。
A
B
C
则有 BD= CD(中线的意义)
D
在△ABD和△ACD中
证明:过点A作BC边上的中线AD,
交BC于点D.
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法二
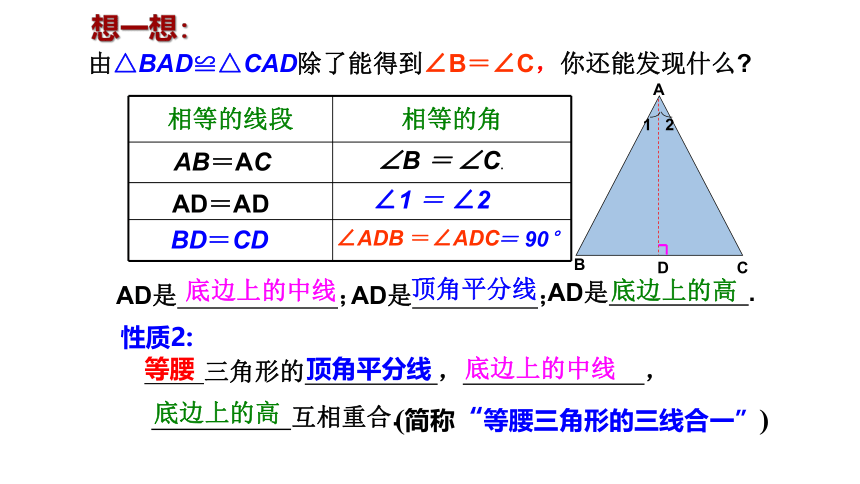
想一想:
由△BAD≌△CAD除了能得到∠B=∠C,你还能发现什么
相等的线段 相等的角
B
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠1 = ∠2
A
D
∠ADB =∠ADC
1 2
= 90°
AD是 ;
AD是 ;
AD是 .
底边上的中线
顶角平分线
底边上的高
性质2:
三角形的 , ,
互相重合.
顶角平分线
等腰
底边上的中线
底边上的高
(简称“等腰三角形的三线合一”)
1.∵AB=AC, ∠1=∠2 (已知)
∴ , .( )
2.∵AB=AC, BD=CD (已知)
∴ , .( )
3.∵AB=AC, AD⊥BC (已知)
∴ , .( )
A
B
C
1
2
D
等腰三角形的 与 ,
互相重合.
顶角平分线
底边上的中线
底边上的高
(简称“等腰三角形的三线合一”)
等腰三角形的三线合一
性质2:
AD⊥BC
BD=CD
BD=CD
∠1=∠2
等腰三角形的三线合一
等腰三角形的三线合一
∠1=∠2
AD⊥BC
等腰三角形是轴对称图形.它的对称轴是:
性质3:
所在的直线.
底边上的中线(或顶角平分线,底边上的高)
等腰三角形的对称轴是底边的垂直平分线 . ( )
判断题:
√
D
思考:等腰三角形是轴对称图形吗?如果是,它的对称
轴是什么?
例题1、已知等腰△ABC中,AB=AC,∠B=70 ,求∠C和∠A的度数.
A
C
B
70
70
解(1) 因为 AB=AC(已知),
所以 ∠C= ∠ B(等边对等角)
由 ∠ B=70°(已知),
得 ∠ C=70°.
(2)因为 ∠ B= ∠ C=70°
又∠ A+ ∠ B+ ∠ C=180°(三角形的内角和等于180°).
所以 ∠ A=180°-70°-70°=40°
例题2:已知,AB=AC,∠BAC=110 ,
AD是△ABC的中线.
⑴求∠1的度数;
⑵求∠ADC的度数
解(1)∵AB=AC,AD是△ABC底边上的中线(已知)
∴∠1= ∠BAC (等腰三角形的三线合一)
∵∠BAC=110 (已知)
∴∠1= ×110 =55 (等式性质)
⑵∵ AB=AC,AD是△ABC底边上的中线(已知)
∴AD⊥BC(等腰三角形的三线合一)
∴∠ADC=90°(垂直的意义)
B
C
D
1
2
A
关于撑伞的数学问题
已知:如图,AB=AC,DB=DC
问: AD与BC有什么关系?
猜想:AD垂直平分BC
∴△ABD≌△ACD(SSS)
∴∠BAD=∠CAD
∴AD垂直平分BC
在⊿ABD和⊿ACD中
证明:
A
B
C
D
课本练习
1.将“等腰三角形三线合一”的性质用符号表示:
(1)“等腰三角形的顶角平分线平分底边并且垂直于底边”.在△ABC 中,如果AB=AC,∠1= ∠2,那么____ =____且___
(2)“等腰三角形底边上的中线垂直于底边,并且平分顶角”.在△ABC中,如果 AB=AC, ____,那么____ ,且____
(3)“等腰三角形底边上的高平分底边和顶角”.在△ABC 中,如果 AB=AC,____,那么____,且____
2.如图,已知AB=AC,AD=AE。说明DE∥BC的理由
解:因为AB=AC(已知)
所以∠B=∠C( )
因为AD=AE(已知)
所以∠ADE=∠AED( )
因为∠A+∠AED+∠ADE=180 °
∠A+∠B+∠C=180 °(三角形内角和为180 °)
所以∠AED+∠ADE=∠B+∠C (等式性质)
所以2∠ADE=2∠B
所以∠ADE=∠B(等式性质)
所以DE∥BC(同位角相等,两直线平行)
等边对等角
等边对等角
3.小明练习册上的一个等腰三角形被墨迹污染了,
只有它的底边AB和∠B还保留着,
请你画出练习册上原来的等腰三角形的形状
随堂检测
1.等腰三角形一个角为70°,它的另外两个角
为 ;
70°,40°或 55°,55°
35°,35°
2.等腰三角形一个角为110°,它的另外两个角为 .
3.如图, AB=AC ,AD⊥BC交BC于点
D,BD=5,∠1=20°,那么BC的长度
为 ,∠BAC= .
10
40°
A
B
C
1
2
D
20°
5
(1)∵AB=AC,AD⊥BC(已知)
∴BD=CD= BC (等腰三角形的三线合一)
(2)∵AB=AC,AD⊥BC(已知)
∴∠1=∠2= ∠BAC (等腰三角形的三线合一)
4. 如图,在△ABC中,AB=AC, ∠A=50°, 求∠ B, ∠ C的度数.
解:
在△ABC中,
∵ AB=AC(已知)
∴ ∠ B=∠ C
(等边对等角)
∵∠ A+ ∠ B+∠ C=180°
(三角形的内角和为180 ° )
且∠ A=50 ° (已知)
∴
(等式性质)
50°
5.填空:在△ABC中,AB=AC, D 在BC上,
(1)、如果AD⊥BC,那么∠BAD = ∠______,
BD = ______
(2)、如果∠BAD= ∠CAD,那么AD⊥___, BD = ____
(3)、如果BD=CD。那么∠BAD =∠ _____, AD⊥___,
∠ADB =∠ _____=___°
D
CAD
CD
BC
CD
CAD
BC
ADC
90
等腰三角形的有关概念:
性质1:等腰三角形的两底角相等.
(等边对等角)
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
(等腰三角形的三线合一)
课堂小结:
性质2:
等腰三角形是轴对称图形,它的对称轴是:底边上的中线(或顶角平分线,底边上的高)所在的直线.
性质3:
腰
A
B
C
腰
底边
顶角
底角
底角
A
B
C
1
2
D
2022-2023学年七年级数学下册同步精品课堂(沪教版)
14.5等腰三角形的性质
第 14章 三角形
3、在你们的印象里,什么样的三角形叫做等腰三角形?
有两条边相等的三角形叫做等腰三角形
2、上面三个三角形按边分类是什么样的三角形
1、上面三个三角形按角分类是什么样的三角形
复习回顾:
如图:在△ABC中,AB=AC,则△ABC就是等腰三角形
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边都叫做腰。
腰
腰
底边
(2)另一边叫底边。
顶角
底角
底角
(3)两腰的夹角∠A叫顶角。
(4)腰与底边夹角∠B、∠C叫底角。
等腰三角形再认识
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC,
说明∠B= C的理由.
猜想
A
B
C
D
问题
等腰三角形的两个底角具有怎样的大小关系
操作
在纸上画一个等腰三角形ABC,其中AB=AC,再画出顶角的平分线AD,设AD与BC 相交于点 D(图14-37)
把 △ABC 纸片剪下,将△ABD 沿着直线AD翻折因为∠BAD= ∠ CAD,所以将 △ABC 沿着AD翻折后射线AB与射线AC 叠合由于 AB=AC,因此线段AB与线段AC 重合,于是点 B 与点 C 重合。又因为点 D 与点 D重合,所以线段BD与线段CD也重合(图14 -38)因此∠ B= ∠ C.
归纳结论
等腰三角形的两个底角相等。
性质1
(简称“等边对等角”)
用符号语言表示为:
A
B
C
∵AB=AC(已知)
∴∠B=∠C( )
等边对等角
A
B
C
则有∠1= ∠2(角平分线的意义)
D
1
2
在△ABD和△ACD中
证明: 过点A作∠BAC的角平分
线AD,交BC于点D.
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
我们可以直接利用全等三角形对等腰三角形的性质进行说理。
A
B
C
则有 BD= CD(中线的意义)
D
在△ABD和△ACD中
证明:过点A作BC边上的中线AD,
交BC于点D.
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法二
想一想:
由△BAD≌△CAD除了能得到∠B=∠C,你还能发现什么
相等的线段 相等的角
B
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠1 = ∠2
A
D
∠ADB =∠ADC
1 2
= 90°
AD是 ;
AD是 ;
AD是 .
底边上的中线
顶角平分线
底边上的高
性质2:
三角形的 , ,
互相重合.
顶角平分线
等腰
底边上的中线
底边上的高
(简称“等腰三角形的三线合一”)
1.∵AB=AC, ∠1=∠2 (已知)
∴ , .( )
2.∵AB=AC, BD=CD (已知)
∴ , .( )
3.∵AB=AC, AD⊥BC (已知)
∴ , .( )
A
B
C
1
2
D
等腰三角形的 与 ,
互相重合.
顶角平分线
底边上的中线
底边上的高
(简称“等腰三角形的三线合一”)
等腰三角形的三线合一
性质2:
AD⊥BC
BD=CD
BD=CD
∠1=∠2
等腰三角形的三线合一
等腰三角形的三线合一
∠1=∠2
AD⊥BC
等腰三角形是轴对称图形.它的对称轴是:
性质3:
所在的直线.
底边上的中线(或顶角平分线,底边上的高)
等腰三角形的对称轴是底边的垂直平分线 . ( )
判断题:
√
D
思考:等腰三角形是轴对称图形吗?如果是,它的对称
轴是什么?
例题1、已知等腰△ABC中,AB=AC,∠B=70 ,求∠C和∠A的度数.
A
C
B
70
70
解(1) 因为 AB=AC(已知),
所以 ∠C= ∠ B(等边对等角)
由 ∠ B=70°(已知),
得 ∠ C=70°.
(2)因为 ∠ B= ∠ C=70°
又∠ A+ ∠ B+ ∠ C=180°(三角形的内角和等于180°).
所以 ∠ A=180°-70°-70°=40°
例题2:已知,AB=AC,∠BAC=110 ,
AD是△ABC的中线.
⑴求∠1的度数;
⑵求∠ADC的度数
解(1)∵AB=AC,AD是△ABC底边上的中线(已知)
∴∠1= ∠BAC (等腰三角形的三线合一)
∵∠BAC=110 (已知)
∴∠1= ×110 =55 (等式性质)
⑵∵ AB=AC,AD是△ABC底边上的中线(已知)
∴AD⊥BC(等腰三角形的三线合一)
∴∠ADC=90°(垂直的意义)
B
C
D
1
2
A
关于撑伞的数学问题
已知:如图,AB=AC,DB=DC
问: AD与BC有什么关系?
猜想:AD垂直平分BC
∴△ABD≌△ACD(SSS)
∴∠BAD=∠CAD
∴AD垂直平分BC
在⊿ABD和⊿ACD中
证明:
A
B
C
D
课本练习
1.将“等腰三角形三线合一”的性质用符号表示:
(1)“等腰三角形的顶角平分线平分底边并且垂直于底边”.在△ABC 中,如果AB=AC,∠1= ∠2,那么____ =____且___
(2)“等腰三角形底边上的中线垂直于底边,并且平分顶角”.在△ABC中,如果 AB=AC, ____,那么____ ,且____
(3)“等腰三角形底边上的高平分底边和顶角”.在△ABC 中,如果 AB=AC,____,那么____,且____
2.如图,已知AB=AC,AD=AE。说明DE∥BC的理由
解:因为AB=AC(已知)
所以∠B=∠C( )
因为AD=AE(已知)
所以∠ADE=∠AED( )
因为∠A+∠AED+∠ADE=180 °
∠A+∠B+∠C=180 °(三角形内角和为180 °)
所以∠AED+∠ADE=∠B+∠C (等式性质)
所以2∠ADE=2∠B
所以∠ADE=∠B(等式性质)
所以DE∥BC(同位角相等,两直线平行)
等边对等角
等边对等角
3.小明练习册上的一个等腰三角形被墨迹污染了,
只有它的底边AB和∠B还保留着,
请你画出练习册上原来的等腰三角形的形状
随堂检测
1.等腰三角形一个角为70°,它的另外两个角
为 ;
70°,40°或 55°,55°
35°,35°
2.等腰三角形一个角为110°,它的另外两个角为 .
3.如图, AB=AC ,AD⊥BC交BC于点
D,BD=5,∠1=20°,那么BC的长度
为 ,∠BAC= .
10
40°
A
B
C
1
2
D
20°
5
(1)∵AB=AC,AD⊥BC(已知)
∴BD=CD= BC (等腰三角形的三线合一)
(2)∵AB=AC,AD⊥BC(已知)
∴∠1=∠2= ∠BAC (等腰三角形的三线合一)
4. 如图,在△ABC中,AB=AC, ∠A=50°, 求∠ B, ∠ C的度数.
解:
在△ABC中,
∵ AB=AC(已知)
∴ ∠ B=∠ C
(等边对等角)
∵∠ A+ ∠ B+∠ C=180°
(三角形的内角和为180 ° )
且∠ A=50 ° (已知)
∴
(等式性质)
50°
5.填空:在△ABC中,AB=AC, D 在BC上,
(1)、如果AD⊥BC,那么∠BAD = ∠______,
BD = ______
(2)、如果∠BAD= ∠CAD,那么AD⊥___, BD = ____
(3)、如果BD=CD。那么∠BAD =∠ _____, AD⊥___,
∠ADB =∠ _____=___°
D
CAD
CD
BC
CD
CAD
BC
ADC
90
等腰三角形的有关概念:
性质1:等腰三角形的两底角相等.
(等边对等角)
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
(等腰三角形的三线合一)
课堂小结:
性质2:
等腰三角形是轴对称图形,它的对称轴是:底边上的中线(或顶角平分线,底边上的高)所在的直线.
性质3:
腰
A
B
C
腰
底边
顶角
底角
底角
A
B
C
1
2
D
