北师大版七年级数学下册 1. 6完全平方公式课后测评 (无答案)
文档属性
| 名称 | 北师大版七年级数学下册 1. 6完全平方公式课后测评 (无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 118.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 16:04:02 | ||
图片预览


文档简介
第一章整式的乘除 6完全平方公式课后测评
一、单选题(共 10 小题)
1、下列计算正确的是( )
A.a·a3=a3 B.a6÷a2=a3
C.(a3)2=a6 D.
2、x2+mx+16是一个完全平方式,则m的值为( )
A.4 B.8 C.4或﹣4 D.8或﹣8
3、已知(x-2021)2 +(x-2023)2 =50,则(x-2022)2的值为( )
A.24 B.23 C.22 D.无法确定
4、如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,则剩下的钢板的面积为( )
A. B. C. D.
5、已知,,,那么的值等于( )
A.0 B.1 C.2 D.3
6、若等式成立,则M是( )
A. B. C.- D.-
7、若,,则的值为()
A.40 B.36 C.32 D.30
8、计算:(a-b+3)(a+b-3)=( )
A.a2+b2-9 B.a2-b2-6b-9
C.a2-b2+6b-9 D.a2+b2-2ab+6a+6b+9
9、如果,那么a.b的值分别为( )
A.2;4 B.5;-25 C.-2;25 D.-5;25
10、已知,,则的值是( )
A.7 B.8 C.9 D.12
二、填空题(共 10 小题)
1、小明同学在做数学作业时发现一道数学题有部分内容被墨水污染了:“先化简,再求值, 其中=“■”小明翻开答案看到这题的结果是7. 你能帮他确定出被墨水污染了的部分内容“■”= _________.
2、若x2-2(m-3)x+16是完全平方式,则m的值为________.
3、,则______.
4、已知,,则的值等于_____.
5、如图,有多个长方形和正方形的卡片,图①是选取了2块不同的卡片,拼成的一个图形,借助图中阴影部分面积的不同表示可以用来验证等式a(a+b)=a2+ab成立,根据图②,利用面积的不同表示方法,仿照上边的式子写出一个等式______________________.
6、若,则的值为 _______.
7、已知,如果,,那么的值为______.
8、若实数,满足,则代数式的值是____.
9、已知,,那么的值为 __.
10、多项式x2+1添加一个单项式后可变为完全平方式,则添加的单项式可以是______.(任写一个符合条件的即可)
三、解答题(共 6 小题)
1、已知正实数x、y,满足(x+y)2=25,xy=4.
(1)求x2+y2的值;
(2)若m=(x﹣y)2时,4a2+na+m是完全平方式,求n的值.
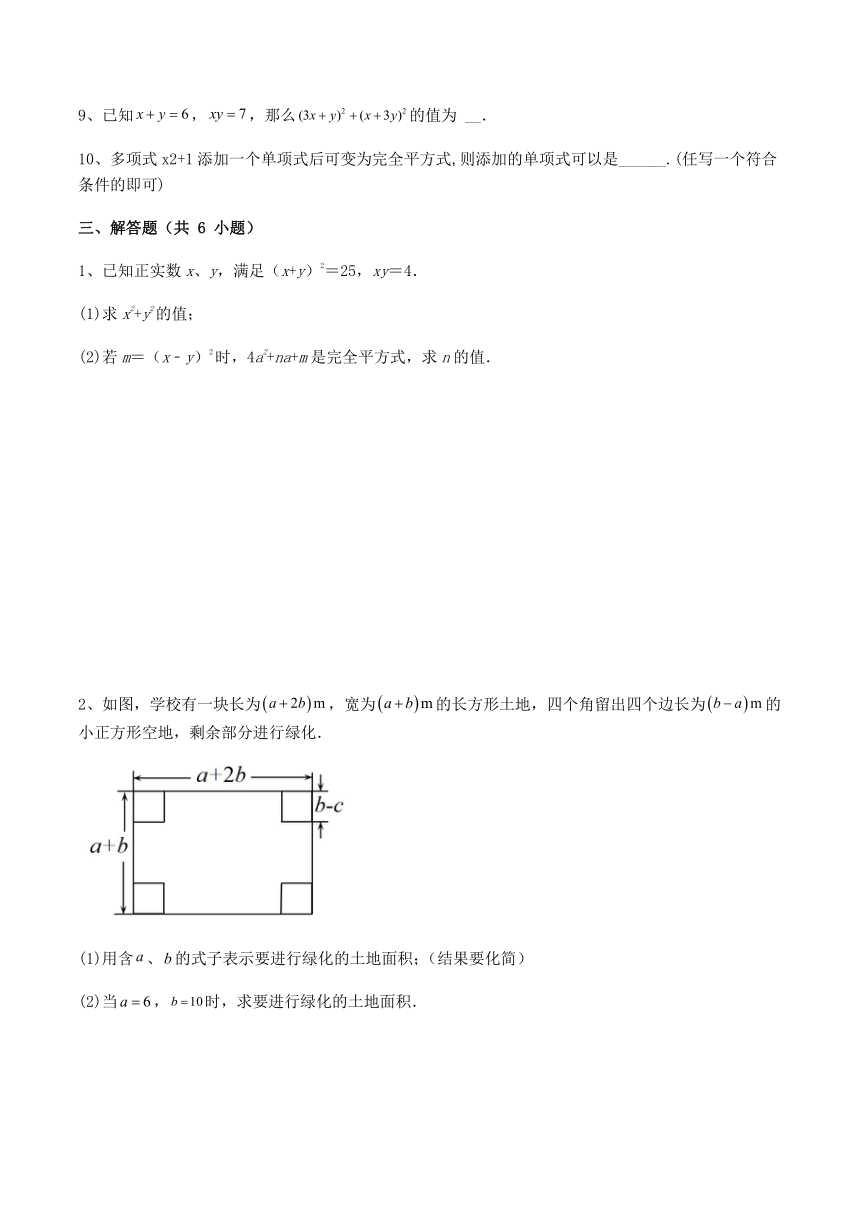
2、如图,学校有一块长为,宽为的长方形土地,四个角留出四个边长为的小正方形空地,剩余部分进行绿化.
(1)用含、的式子表示要进行绿化的土地面积;(结果要化简)
(2)当,时,求要进行绿化的土地面积.
3、利用我们学过的完全平方公式与不等式知识能解决方程或代数式的一些问题,阅读下列两则材料:
材料一:已知m2-2mn+2n2-8n+16=0,求m、n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2mn+n2)+(n2-8n+16)=0,
∴(m-n)2+(n-4)2=0,
∵(m-n)2≥0,(n-4)2≥0
∴(m-n)2=0,(n-4)2=0
∴m=n=4.
材料二:探索代数式x2+4x+2与-x2+2x+3是否存在最大值或最小值?
①x2+4x+2=(x2+4x+4)-2=(x+2)2-2,∵(x+2)2≥0,∴x2+4x+2=(x+2)2-2≥-2.
∴代数式x2+4x+2有最小值-2;
②-x2+2x+3=-(x2-2x+1)+4=-(x-1)2+4,∵-(x-1)2≤0,∴-x2+2x+3=-(x-1)2+4≤4.
∴代数式-x2+2x+3有最大值4.
学习方法并完成下列问题:
(1)代数式x2-6x+3的最小值为_______;
(2)如图,在紧靠围墙的空地上,利用围墙及一段长为100米的木栅栏围成一个长方形花圃,为了设计一个尽可能大的花圃,设长方形垂直于围墙的一边长度为x米,则花圃的最大面积是多少?
已知△ABC的三条边的长度分别为a,b,c,且a2+b2+74=10a+14b,且c为正整数,求△ABC周长的最小值.
4、如图,甲长方形的两边长分别为m+1,m+5;乙长方形的两边长分别为m+2,m+4.(其中m为正整数).
(1)图中的甲长方形的面积= ,乙长方形的面积= ,比较: (填“<”、“=”或“>”),并说明理由;
(2)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积S与图中的甲长方形面积的差(即S﹣)是一个常数,求出这个常数.
5、要比较a,b两个数的大小,有时可以通过比较a﹣b与0的大小来解决.如果a-b>0,则a>b;如果a-b=0,则a=b.如果a-b<0,则a<b.若,,试比较x,y的大小.
6、先化简,再求值:,其中.
一、单选题(共 10 小题)
1、下列计算正确的是( )
A.a·a3=a3 B.a6÷a2=a3
C.(a3)2=a6 D.
2、x2+mx+16是一个完全平方式,则m的值为( )
A.4 B.8 C.4或﹣4 D.8或﹣8
3、已知(x-2021)2 +(x-2023)2 =50,则(x-2022)2的值为( )
A.24 B.23 C.22 D.无法确定
4、如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,则剩下的钢板的面积为( )
A. B. C. D.
5、已知,,,那么的值等于( )
A.0 B.1 C.2 D.3
6、若等式成立,则M是( )
A. B. C.- D.-
7、若,,则的值为()
A.40 B.36 C.32 D.30
8、计算:(a-b+3)(a+b-3)=( )
A.a2+b2-9 B.a2-b2-6b-9
C.a2-b2+6b-9 D.a2+b2-2ab+6a+6b+9
9、如果,那么a.b的值分别为( )
A.2;4 B.5;-25 C.-2;25 D.-5;25
10、已知,,则的值是( )
A.7 B.8 C.9 D.12
二、填空题(共 10 小题)
1、小明同学在做数学作业时发现一道数学题有部分内容被墨水污染了:“先化简,再求值, 其中=“■”小明翻开答案看到这题的结果是7. 你能帮他确定出被墨水污染了的部分内容“■”= _________.
2、若x2-2(m-3)x+16是完全平方式,则m的值为________.
3、,则______.
4、已知,,则的值等于_____.
5、如图,有多个长方形和正方形的卡片,图①是选取了2块不同的卡片,拼成的一个图形,借助图中阴影部分面积的不同表示可以用来验证等式a(a+b)=a2+ab成立,根据图②,利用面积的不同表示方法,仿照上边的式子写出一个等式______________________.
6、若,则的值为 _______.
7、已知,如果,,那么的值为______.
8、若实数,满足,则代数式的值是____.
9、已知,,那么的值为 __.
10、多项式x2+1添加一个单项式后可变为完全平方式,则添加的单项式可以是______.(任写一个符合条件的即可)
三、解答题(共 6 小题)
1、已知正实数x、y,满足(x+y)2=25,xy=4.
(1)求x2+y2的值;
(2)若m=(x﹣y)2时,4a2+na+m是完全平方式,求n的值.
2、如图,学校有一块长为,宽为的长方形土地,四个角留出四个边长为的小正方形空地,剩余部分进行绿化.
(1)用含、的式子表示要进行绿化的土地面积;(结果要化简)
(2)当,时,求要进行绿化的土地面积.
3、利用我们学过的完全平方公式与不等式知识能解决方程或代数式的一些问题,阅读下列两则材料:
材料一:已知m2-2mn+2n2-8n+16=0,求m、n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2mn+n2)+(n2-8n+16)=0,
∴(m-n)2+(n-4)2=0,
∵(m-n)2≥0,(n-4)2≥0
∴(m-n)2=0,(n-4)2=0
∴m=n=4.
材料二:探索代数式x2+4x+2与-x2+2x+3是否存在最大值或最小值?
①x2+4x+2=(x2+4x+4)-2=(x+2)2-2,∵(x+2)2≥0,∴x2+4x+2=(x+2)2-2≥-2.
∴代数式x2+4x+2有最小值-2;
②-x2+2x+3=-(x2-2x+1)+4=-(x-1)2+4,∵-(x-1)2≤0,∴-x2+2x+3=-(x-1)2+4≤4.
∴代数式-x2+2x+3有最大值4.
学习方法并完成下列问题:
(1)代数式x2-6x+3的最小值为_______;
(2)如图,在紧靠围墙的空地上,利用围墙及一段长为100米的木栅栏围成一个长方形花圃,为了设计一个尽可能大的花圃,设长方形垂直于围墙的一边长度为x米,则花圃的最大面积是多少?
已知△ABC的三条边的长度分别为a,b,c,且a2+b2+74=10a+14b,且c为正整数,求△ABC周长的最小值.
4、如图,甲长方形的两边长分别为m+1,m+5;乙长方形的两边长分别为m+2,m+4.(其中m为正整数).
(1)图中的甲长方形的面积= ,乙长方形的面积= ,比较: (填“<”、“=”或“>”),并说明理由;
(2)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积S与图中的甲长方形面积的差(即S﹣)是一个常数,求出这个常数.
5、要比较a,b两个数的大小,有时可以通过比较a﹣b与0的大小来解决.如果a-b>0,则a>b;如果a-b=0,则a=b.如果a-b<0,则a<b.若,,试比较x,y的大小.
6、先化简,再求值:,其中.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
