人教A版(2019)选择性必修第三册 第八章 统计套题(含解析)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册 第八章 统计套题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 08:46:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023年高中数学统计套题
一.选择题(共8小题)
1.空气质量指数是评估空气质量状况的一组数字,空气质量指数划分为[0,50)、[50,100)、[100,150)、[150,200)、[200,300)和[300,500]六档,分别对应“优”、“良”、“轻度污染”、“中度污染”、“重度污染”和“严重污染”六个等级.如图是某市2月1日至14日连续14天的空气质量指数趋势图,则下面说法中正确的是( )
A.这14天中有5天空气质量为“中度污染”
B.从2日到5日空气质量越来越好
C.这14天中空气质量指数的中位数是214
D.连续三天中空气质量指数方差最小是5日到7日
2.甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(图1),茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(图2)完好,则( )
A.甲的单场平均得分比乙低
B.乙的60%分位数为19
C.甲、乙的极差均为11
D.乙得分的中位数是16.5
3.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;方差分别为,则下面正确的是( )
A. B.
C. D.
4.某市质量检测部门从辖区内甲、乙两个地区的食品生产企业中分别随机抽取9家企业,根据食品安全管理考核指标对抽到的企业进行考核,并将各企业考核得分整理成如下的茎叶图.由茎叶图所给信息,可判断以下结论中正确是( )
A.若a=2,则甲地区考核得分的极差大于乙地区考核得分的极差
B.若a=4,则甲地区考核得分的平均数小于乙地区考核得分的平均数
C.若a=5,则甲地区考核得分的方差小于乙地区考核得分的方差
D.若a=6,则甲地区考核得分的中位数小于乙地区考核得分的中位数
5.关于统计数据的分析,有以下几个结论,其中正确的是( )
A.将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化
B.样本数据9、3、5、7、12、13、1、8、10、18的中位数是8或9
C.在刻画回归模型的拟合效果时,相关指数R2的值越大,说明拟合的效果越好
D.在调查影院中观众观后感时,从20排中(每排人数相同)每排任意抽取一人进行调查是系统抽样法
6.根据变量x与y的对应关系(如表),求得y关于x的线性回归方程为y=6.5x+17.5,则表中m的值为( )
x 2 4 5 6 8
y 30 40 m 50 70
A.60 B.55 C.50 D.45
7.已知变量的关系可以用模型y=kemx拟合,设z=lny,其变换后得到一组数据如下.由表可得线性回归方程z=3x+a,则k=( )
x 1 2 3 4 5
z 2 4 5 10 14
A.e﹣3 B.e﹣2 C.e2 D.e3
8.关于线性回归的描述,下列说法不正确的是( )
A.回归直线方程中变量x,y成正相关关系
B.相关系数r越接近1,相关程度越强
C.回归直线方程中变量x,y成正相关关系
D.残差平方和越小,拟合效果越好
二.多选题(共4小题)
(多选)9.给定数5,4,3,5,3,2,2,3,1,2,则这组数据的( )
A.中位数为3 B.方差为
C.众数为3 D.85%分位数为4.5
(多选)10.树人中学2006班某科研小组,持续跟踪调查了他们班全体同学一学期中16周锻炼身体的时长,经过整理得到男生、女生各周锻炼身体的平均时长(单位:h)的数据如下:
男生:6.3、7.4、7.6、8.1、8.2、8.2、8.5、8.6、8.6、8.6、8.6、9.0、9.2、9.3、9.8、10.1;
女生:5.1、5.6、6.0、6.3、6.5、6.8、7.2、7.3、7.5、7.7、8.1、8.2、8.4、8.6、9.2、9.4.
以下判断中正确的是( )
A.女生每周锻炼身体的平均时长的平均值等于8
B.男生每周锻炼身体的平均时长的80%分位数是9.2
C.男生每周锻炼身体的平均时长大于9h的概率的估计值为0.3125
D.与男生相比,女生每周锻炼身体的平均时长波动性比较大
(多选)11.下列关于成对数据的统计说法正确的有( )
A.若当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关
B.样本相关系数r的绝对值大小可以反映成对样本数据之间线性相关的程度
C.通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据
D.决定系数R2越大,模型的拟合效果越差
(多选)12.某校抽取了某班20名学生的化学成绩,并将他们的成绩制成如下所示的表格.
成绩 60 65 70 75 80 85 90
人数 2 3 3 5 4 2 1
下列结论正确的是( )
A.这20人成绩的众数为75
B.这20人成绩的极差为30
C.这20人成绩的25%分位数为65
D.这20人成绩的平均数为75
三.填空题(共4小题)
13.某高中的三个年级共有学生2000人,其中高一600人,高二680人,高三720人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 .
14.某班共有50名学生,在期末考试中,小明因病未参加数学考试.参加考试的49名学生的数学成绩的方差为2.在评估数学成绩时,老师把小明的数学成绩按这49名学生的数学成绩的平均数来算,那么全班50名学生的数学成绩的标准差为 .
15.设一组样本数据x1,x2,…,x8的方差为6,则数据3x1+1,3x2+1,…,3x8+1的方差是 .
16.身体质量指数,也就是BMI指数,简称体质指数,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.某校为了解该校学生的身体健康情况,从某班随机抽取20名学生进行调查,得到这20名学生的BMI指数分别是15,15.3,15.6,15.9,16.2,16.6,17.5,17.8,18.2,18.7,19.3,19.5,20.3,21.1,21.5,22.7,22.9,23.1,23.4,23.5,则这组数据的第65百分位数是 .
四.解答题(共6小题)
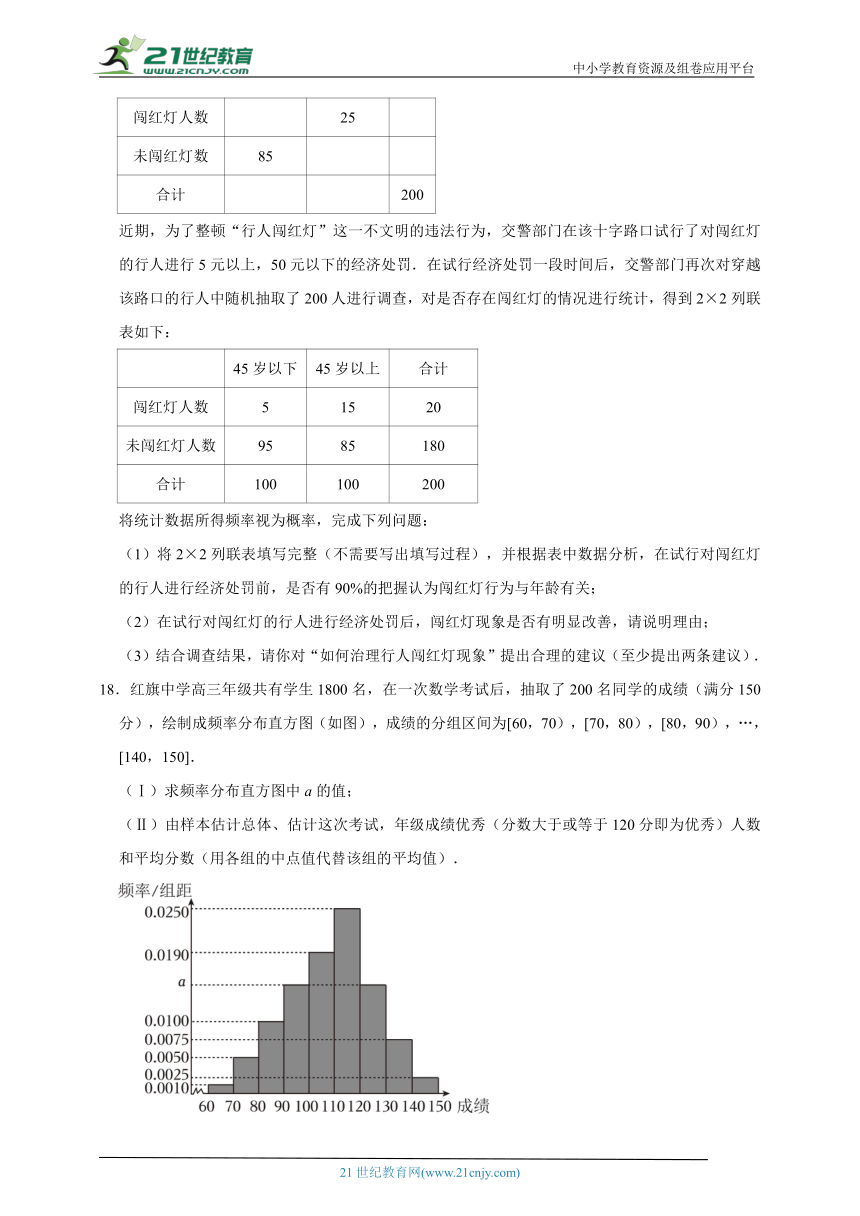
17.某市从2020年5月1日开始,若电子警察抓拍到机动车不礼让行人的情况后,交警部门将会对不礼让行人的驾驶员进行扣3分,罚款200元的处罚,并在媒体上曝光.但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患和机动车通畅率降低的情况.交警部门在某十字路口根据以往的监测数据,得到行人闯红灯的概率为0.2,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯的情况进行统计,得到2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 25
未闯红灯数 85
合计 200
近期,为了整顿“行人闯红灯”这一不文明的违法行为,交警部门在该十字路口试行了对闯红灯的行人进行5元以上,50元以下的经济处罚.在试行经济处罚一段时间后,交警部门再次对穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯的情况进行统计,得到2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 5 15 20
未闯红灯人数 95 85 180
合计 100 100 200
将统计数据所得频率视为概率,完成下列问题:
(1)将2×2列联表填写完整(不需要写出填写过程),并根据表中数据分析,在试行对闯红灯的行人进行经济处罚前,是否有90%的把握认为闯红灯行为与年龄有关;
(2)在试行对闯红灯的行人进行经济处罚后,闯红灯现象是否有明显改善,请说明理由;
(3)结合调查结果,请你对“如何治理行人闯红灯现象”提出合理的建议(至少提出两条建议).
18.红旗中学高三年级共有学生1800名,在一次数学考试后,抽取了200名同学的成绩(满分150分),绘制成频率分布直方图(如图),成绩的分组区间为[60,70),[70,80),[80,90),…,[140,150].
(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)由样本估计总体、估计这次考试,年级成绩优秀(分数大于或等于120分即为优秀)人数和平均分数(用各组的中点值代替该组的平均值).
19.网络直播带货助力乡村振兴,它作为一种新颖的销售土特产的方式,受到社会各界的追捧.某直播间开展地标优品带货直播活动,其主播直播周期次数x(其中10场为一个周期)与产品销售额y(千元)的数据统计如下:
直播周期数x 1 2 3 4 5
产品销售额y(千元) 3 7 15 30 40
根据数据特点,甲认为样本点分布在指数型曲线y=2bx+a的周围,据此他对数据进行了一些初步处理.如下表:
3.7 55 382 65 978 101
其中zi=log2yi,=
(1)请根据表中数据,建立y关于x的回归方程(系数精确到0.01);
(2)①乙认为样本点分布在直线y=mx+n的周围,并计算得回归方程为=9.7x﹣10.1,以及该回归模型的相关指数R乙2=0.98,试比较甲、乙两人所建立的模型,谁的拟合效果更好?
②由①所得的结论,计算该直播间欲使产品销售额达到8万元以上,直播周期数至少为多少?(最终答案精确到1)
附:对于一组数据 (u1,v1)(u2,v2),…,(un,vn),其回归直线=+u的斜率和截距的最小二乘估计分别为=,=,相关系数:R2=1﹣.
20.据统计,某校高三打印室1﹣4月份购买的打印纸的箱数如表:
月份代号t 1 2 3 4
打印纸的数量y(箱) 60 65 70 85
(1)求相关系数r,并从r的角度分析能否用线性回归模型拟合y与t的关系(若|r|≥0.75,则线性相关程度很强,可用线性回归模型拟合);
(2)建立y关于t的回归方程,并用其预测5月份该校高三打印室需购买的打印纸约为多少箱.
参考公式:对于一组具有线性相关关系的数据(xi,yi)(i=1,2,3, ,n),其回归直线的斜率和截距的最小二乘估计分别为=,.
相关系数,参考数据:
21.中国男篮历史上曾12次参加亚运会,其中8次夺得金牌,是亚运会夺冠次数最多的球队.第19届亚运会将于2023年9月23日至10月8日在杭州举办.
(1)为了解喜爱篮球运动是否与性别有关,某学校随机抽取了男生和女生各100名进行调查,得到2×2列联表如下:
喜爱篮球 不喜爱篮球合计
男生 65 35 100
女生 25 75 100
合计 90 110 200
依据小概率值α=0.001的独立性检验,能否认为喜爱篮球运动与性别有关?
(2)校篮球队中的甲、乙、丙三名球员将进行传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,第n次触球者是甲的概率记为Pn,即P1=1.
(i)求P3,P4,并证明:为等比数列;
(ii)比较第15次触球者是甲与第15次触球者是乙的概率的大小.
参考公式:,其中n=a+b+c+d为样本容量.
参考数据:
P(K2≥k) 0.10 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
22.2022年11月17日,由工业和信息化部、安徽省人民政府共同主办的第十七届“中国芯”集成电路产业大会在合肥成功举办.此次大会以“强芯固基以质为本”为主题,旨在培育壮大我国集成电路产业,夯实产业基础、营造良好产业生态.2022年,全国芯片研发单位相比2006年增加194家,提交芯片数量增加299个,均增长超过6倍.某芯片研发单位用在“A芯片”上研发费用占本单位总研发费用的百分比y(%)如表所示.
年份 2016 2017 2018 2019 2020 2021 2022
年份代码 1 2 3 4 5 6 7
y 20% 30% 32% 39% 42% 46% 50%
(1)根据表中的数据,作出相应的折线图;并结合相关数据,计算相关系数r,并推断y与t线性相关程度;(已知:0.8≤|r|≤1,则认为y与t线性相关很强;0.3≤|r|<0.8,则认为y与t线性相关一般;|r|<0.3,则认为y与t线性相关较弱)
(2)求出y与t的回归直线方程(保留一位小数);
(3)请判断,若2024年用在“A芯片”上研发费用不低于295万元,则该单位2024年芯片研发的总费用预算为500万元是否符合研发要求?
附:相关数据:,,,.
相关计算公式:①相关系数;
在回归直线方程中,,.
2023年高中数学统计套题
参考答案与试题解析
一.选择题(共8小题)
1.空气质量指数是评估空气质量状况的一组数字,空气质量指数划分为[0,50)、[50,100)、[100,150)、[150,200)、[200,300)和[300,500]六档,分别对应“优”、“良”、“轻度污染”、“中度污染”、“重度污染”和“严重污染”六个等级.如图是某市2月1日至14日连续14天的空气质量指数趋势图,则下面说法中正确的是( )
A.这14天中有5天空气质量为“中度污染”
B.从2日到5日空气质量越来越好
C.这14天中空气质量指数的中位数是214
D.连续三天中空气质量指数方差最小是5日到7日
【分析】根据题意,由折线图分析数据,由此分析选项是否正确,即可得答案.
【解答】解:根据题意,依次分析选项:
对于A,这14天中有4天空气质量指数在[150,200)之间,则有4天为“中度污染”,A错误;
对于B,从2日到5日空气质量逐渐下降,即空气质量越来越好,B正确;
对于C,将14组数据从小到大排列:80,83,138,155,157,165,179,214,214,221,243,260,263,275,其中位数为(179+214)=196.5,C错误;
对于D,5日到7日的三天,数据相差比较大,则连续三天中空气质量指数方差最小不是5日到7日,D错误.
故选:B.
【点评】本题考查由折线图分析数据,涉及中位数、方差的意义,属于基础题.
2.甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(图1),茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(图2)完好,则( )
A.甲的单场平均得分比乙低
B.乙的60%分位数为19
C.甲、乙的极差均为11
D.乙得分的中位数是16.5
【分析】根据茎叶图、折线图,平均数、中位数、百分数、极差的求法判断各项的正误即可.
【解答】解:A:由茎叶图和折线图,甲比赛得分为{9,12,13,14,15,20,26,28},平均得分为,
乙比赛得分为{9,14,15,16,17,18,19,20},平均得分为,甲高于乙,故A错误;
B:由8×60%=4.8,故乙的60%分位数为17,故B错误;
C:甲的极差为28﹣9=19,乙的极差为20﹣9=11,故C错误;
D:乙得分的中位数是,故D正确.
故选:D.
【点评】本题主要考查了茎叶图的应用,考查了平均数、百分位数、中位数和极差的计算,属于基础题.
3.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;方差分别为,则下面正确的是( )
A. B.
C. D.
【分析】根据直方图求出甲、乙地区用户满意度评分的中位数,并通过两地区用户满意度评分的集中程度即可得到哪个方差小.
【解答】解:由频率分布直方图得:
甲地区:[40,60)的频率为(0.015+0.020)×10=0.35,[60,70)的频率为0.025×10=0.25,
∴甲地区用户满意度评分的中位数,
乙地区:[50,70)的频率为(0.005+0.020)×10=0.25,[70,80)的频率为0.035×10=0.35,
∴乙地区用户满意度评分的中位数,
∴m1<m2,
由直方图可以看出,乙地区用户满意度评分的集中程度比甲地区的高,
∴.
故选:D.
【点评】本题主要考查了频率分布直方图的应用,考查了中位数和方差的计算,属于基础题.
4.某市质量检测部门从辖区内甲、乙两个地区的食品生产企业中分别随机抽取9家企业,根据食品安全管理考核指标对抽到的企业进行考核,并将各企业考核得分整理成如下的茎叶图.由茎叶图所给信息,可判断以下结论中正确是( )
A.若a=2,则甲地区考核得分的极差大于乙地区考核得分的极差
B.若a=4,则甲地区考核得分的平均数小于乙地区考核得分的平均数
C.若a=5,则甲地区考核得分的方差小于乙地区考核得分的方差
D.若a=6,则甲地区考核得分的中位数小于乙地区考核得分的中位数
【分析】根据极差、平均数、中位数的计算方法判断ABD;由波动程度判断C.
【解答】解:对于选项A:甲地区考核得分的极差为94﹣75=19,乙地区考核得分的极差为99﹣74=25,
即甲地区考核得分的极差小于乙地区考核得分的极差,故选项A错误;
对于选项B:甲地区考核得分的平均数为,
乙地区考核得分的平均数为,
即甲地区考核得分的平均数大于乙地区考核得分的平均数,故选项B错误;
对于选项C:甲地区考核得分从小到大排列为:75,78,81,84,85,88,92,93,94,
乙地区考核得分从小到大排列为:74,77,80,83,84,87,91,95,99,
由以上数据可知,乙地区考核得分的波动程度比甲地区考核得分的波动程度大,即甲地区考核得分的方差小于乙地区考核得分的方差,故选项C正确;
对于选项D:由茎叶图可知,甲地区考核得分的中位数为85,乙地区考核得分的中位数为84,即甲地区考核得分的中位数大于乙地区考核得分的中位数,故选项D错误;
故选:C.
【点评】本题主要考查了茎叶图的应用,考查了极差、平均数、中位数的计算,属于基础题.
5.关于统计数据的分析,有以下几个结论,其中正确的是( )
A.将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化
B.样本数据9、3、5、7、12、13、1、8、10、18的中位数是8或9
C.在刻画回归模型的拟合效果时,相关指数R2的值越大,说明拟合的效果越好
D.在调查影院中观众观后感时,从20排中(每排人数相同)每排任意抽取一人进行调查是系统抽样法
【分析】根据平均数与方差、中位数和线性相关系数,以及抽样方法的定义,对选项的问题分析与判断即可.
【解答】解:对于A,将一组数据中的每个数据都减去同一个数后,平均数减小,方差不变,所以选项A错误;
对于B,样本数据按从小到大顺序排列为1、3、5、7、8、9、10、12、13、18,所以中位数是=8.5,选项B错误;
对于C,刻画回归模型的拟合效果时,相关指数R2的值越大,说明拟合的效果越好,选项C正确;
对于D,调查影院中观众观后感时,从20排中(每排人数相同)每排任意抽取一人进行调查是简单随机抽样,不是系统抽样法,选项D错误;
故选:C.
【点评】本题考查了对平均数与方差、中位数和线性相关系数,以及抽样方法的理解与判断问题,是基础题.
6.根据变量x与y的对应关系(如表),求得y关于x的线性回归方程为y=6.5x+17.5,则表中m的值为( )
x 2 4 5 6 8
y 30 40 m 50 70
A.60 B.55 C.50 D.45
【分析】先求得样本点中心,再根据回归直线过样本点中心即可求解.
【解答】解:由表中数据,计算,,
因为回归直线方程过样本中心,
∴,
解得m=60.
故选:A.
【点评】本题考查线性回归方程的运用,解题的关键是利用线性回归方程恒过样本中心点,这是线性回归方程中最常考的知识点.属于基础题.
7.已知变量的关系可以用模型y=kemx拟合,设z=lny,其变换后得到一组数据如下.由表可得线性回归方程z=3x+a,则k=( )
x 1 2 3 4 5
z 2 4 5 10 14
A.e﹣3 B.e﹣2 C.e2 D.e3
【分析】根据样本中心点在回归方程上可得a=﹣2,再利用对数运算法则即可得lnk+mx=3x﹣2,所以k=e﹣2.
【解答】解:由表格数据知,.即样本中心点为(3,7),
由z=3x+a,得a=7﹣3×3=﹣2,
即z=3x﹣2,
所以z=lny=lnk+mx=3x﹣2,即lnk=﹣2,可得k=e﹣2,
故选:B.
【点评】本题考查线性回归方程的运用,解题的关键是利用线性回归方程恒过样本中心点,这是线性回归方程中最常考的知识点.属于基础题.
8.关于线性回归的描述,下列说法不正确的是( )
A.回归直线方程中变量x,y成正相关关系
B.相关系数r越接近1,相关程度越强
C.回归直线方程中变量x,y成正相关关系
D.残差平方和越小,拟合效果越好
【分析】根据线性回归的性质可知:b的正负决定正负相关,可判断选项A,C;根据相关系数的绝对值越接近1,相关性越强,可判断B;残差平方和越小,拟合效果越好,可判断选项D.
【解答】解:对于A,因为回归直线方程中的b<0,所以变量x,y成负相关关系,故选项A错误;
对于B,因为相关系数r的绝对值越接近1,相关度越强,所以当相关系数r越接近1,相关程度越强,故选项B正确;
对于C,因为回归直线方程中的b=1.1>0,所以变量x,y成正相关关系,故选项C正确;
对于D,因为残差平方和越小,拟合效果越好,所以选项D正确,
综上:说法不正确的是A,
故选:A.
【点评】本题主要考查了线性回归方程的应用,属于基础题.
二.多选题(共4小题)
(多选)9.给定数5,4,3,5,3,2,2,3,1,2,则这组数据的( )
A.中位数为3 B.方差为
C.众数为3 D.85%分位数为4.5
【分析】先将数5,4,3,5,3,2,2,3,1,2,按小到大的顺序排列,再逐项判断.
【解答】解:将数5,4,3,5,3,2,2,3,1,2,按小到大的顺序排列为:1,2,2,2,3,3,3,4,5,5,
则这组数据的中位数为,故A正确;
数据中2,3,出现的次数最多,所以众数为2和3,故C错误;
平均数为:,
则方差为,故B正确;
第85%分位数是数据中至少有85%的数据小于或等于该数,因此,从小到大第9个数字为5,故D错误,
故选:AB.
【点评】本题主要考查了中位数,平均数和方差的计算,属于基础题.
(多选)10.树人中学2006班某科研小组,持续跟踪调查了他们班全体同学一学期中16周锻炼身体的时长,经过整理得到男生、女生各周锻炼身体的平均时长(单位:h)的数据如下:
男生:6.3、7.4、7.6、8.1、8.2、8.2、8.5、8.6、8.6、8.6、8.6、9.0、9.2、9.3、9.8、10.1;
女生:5.1、5.6、6.0、6.3、6.5、6.8、7.2、7.3、7.5、7.7、8.1、8.2、8.4、8.6、9.2、9.4.
以下判断中正确的是( )
A.女生每周锻炼身体的平均时长的平均值等于8
B.男生每周锻炼身体的平均时长的80%分位数是9.2
C.男生每周锻炼身体的平均时长大于9h的概率的估计值为0.3125
D.与男生相比,女生每周锻炼身体的平均时长波动性比较大
【分析】根据平均数公式可判断A选项;利用百分位数的定义可判断B选项;利用频率估计概率可判断C选项;利用极差与男生、女生锻炼的平均时长的分布可判断D选项.
【解答】解:对于A选项,由平均数公式可知,
女生每周锻炼身体的平均时长的平均值等于=7.36875(h),A错;
对于B选项,因为16×0.8=12.8,
因此,男生每周锻炼身体的平均时长的80%分位数是9.2h,B对;
对于C选项,男生每周锻炼身体的平均时长大于9h的有4周,
所求概率为,C错;
对于D选项,男生每周锻炼身体的平均时长分布在区间(8,9)内共有8个,女生有4个,
男生每周锻炼身体的平均时长分布在区间(7,10)内的共14个,女生为10个,
男生每周锻炼身体的平均时长的极差为10.1﹣6.3=3.8,女生为9.4﹣5.1=4.3,
据此可知与男生相比,女生每周锻炼身体的平均时长波动性比较大,
所以,与男生相比,女生每周锻炼身体的平均时长波动性比较大,D对.
故选:BD.
【点评】本题主要考查了平均数、极差的计算,考查了古典概型的概率公式,属于中档题.
(多选)11.下列关于成对数据的统计说法正确的有( )
A.若当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关
B.样本相关系数r的绝对值大小可以反映成对样本数据之间线性相关的程度
C.通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据
D.决定系数R2越大,模型的拟合效果越差
【分析】根据题意,由变量间相关关系的定义依次分析选项是否正确,即可得答案.
【解答】解:根据题意,依次分析选项:
对于A,由变量相关的定义,可得A正确;
对于B,样本相关系数r的绝对值越大,样本数据之间线性相关的程度越高,则样本相关系数r的绝对值大小可以反映成对样本数据之间线性相关的程度,B正确;
对于C,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据,C正确;
对于D,系数R2越大,模型的拟合效果越好,D错误.
故选:ABC.
【点评】本题考查变量间的相关关系,涉及回归分析的基本概念,属于基础题.
(多选)12.某校抽取了某班20名学生的化学成绩,并将他们的成绩制成如下所示的表格.
成绩 60 65 70 75 80 85 90
人数 2 3 3 5 4 2 1
下列结论正确的是( )
A.这20人成绩的众数为75
B.这20人成绩的极差为30
C.这20人成绩的25%分位数为65
D.这20人成绩的平均数为75
【分析】根据众数的概念,极差的概念,百分位数的概念,平均数的概念,即可分别求解.
【解答】解:对A选项,∵这20名学生的化学成绩的众数为75,∴A正确;
对B选项,∵这20名学生的化学成绩的极差为90﹣60=30,∴B正确;
对C选项,∵20×25%=5,∴这20人成绩的25%分位数为=67.5,∴C错误;
对D选项,∵这20名学生的化学成绩的平均数为:
=74,∴D错误.
故选:AB.
【点评】本题考众数的概念,极差的概念,百分位数的概念,平均数的概念,属基础题.
三.填空题(共4小题)
13.某高中的三个年级共有学生2000人,其中高一600人,高二680人,高三720人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 15 .
【分析】根据分层抽样原则直接计算即可.
【解答】解:由题意,从全校2000人中抽取50人访谈,按照年级分层,则高一年级应该抽人.
故答案为:15.
【点评】本题主要考查了分层抽样的定义,属于基础题.
14.某班共有50名学生,在期末考试中,小明因病未参加数学考试.参加考试的49名学生的数学成绩的方差为2.在评估数学成绩时,老师把小明的数学成绩按这49名学生的数学成绩的平均数来算,那么全班50名学生的数学成绩的标准差为 .
【分析】先由题意得到,再由数学成绩的标准差为求解.
【解答】解:设参加考试的49名学生的数学成绩为xi(i=1,2,3,...,49),平均成绩为,
由题意得,
则全班50名学生的数学成绩的标准差为:,=,=.
故答案为:.
【点评】本题主要考查了数据标准差的计算,属于基础题.
15.设一组样本数据x1,x2,…,x8的方差为6,则数据3x1+1,3x2+1,…,3x8+1的方差是 54 .
【分析】设x1,x2, ,x8的平均数为,结合x1,x2, ,x8的方差为6,根据平均数和方差的计算公式得到3x1+1,3x2+1, ,3x8+1的平均数和方差.
【解答】解:设x1,x2, ,x8的平均数为,
则x1+x2+…+x8=8,
又,
故3x1+1,3x2+1, ,3x8+1的平均数为,
方差为=.
故答案为:54.
【点评】本题主要考查了方差公式及方差性质的应用,属于基础题.
16.身体质量指数,也就是BMI指数,简称体质指数,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.某校为了解该校学生的身体健康情况,从某班随机抽取20名学生进行调查,得到这20名学生的BMI指数分别是15,15.3,15.6,15.9,16.2,16.6,17.5,17.8,18.2,18.7,19.3,19.5,20.3,21.1,21.5,22.7,22.9,23.1,23.4,23.5,则这组数据的第65百分位数是 20.7 .
【分析】根据百分位数的定义即可求解.
【解答】解:因为20×0.65=13,
所以这组数据的第65百分位数是.
故答案为:20.7.
【点评】本题主要考查百分数的定义,属于基础题.
四.解答题(共6小题)
17.某市从2020年5月1日开始,若电子警察抓拍到机动车不礼让行人的情况后,交警部门将会对不礼让行人的驾驶员进行扣3分,罚款200元的处罚,并在媒体上曝光.但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患和机动车通畅率降低的情况.交警部门在某十字路口根据以往的监测数据,得到行人闯红灯的概率为0.2,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯的情况进行统计,得到2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 25
未闯红灯数 85
合计 200
近期,为了整顿“行人闯红灯”这一不文明的违法行为,交警部门在该十字路口试行了对闯红灯的行人进行5元以上,50元以下的经济处罚.在试行经济处罚一段时间后,交警部门再次对穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯的情况进行统计,得到2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 5 15 20
未闯红灯人数 95 85 180
合计 100 100 200
将统计数据所得频率视为概率,完成下列问题:
(1)将2×2列联表填写完整(不需要写出填写过程),并根据表中数据分析,在试行对闯红灯的行人进行经济处罚前,是否有90%的把握认为闯红灯行为与年龄有关;
(2)在试行对闯红灯的行人进行经济处罚后,闯红灯现象是否有明显改善,请说明理由;
(3)结合调查结果,请你对“如何治理行人闯红灯现象”提出合理的建议(至少提出两条建议).
【分析】(1)根据题意,填写出2×2列联表,利用公式求得K2的值,结合附表,即可得到结论;
(2)求得试行对闯红灯的行人进行经济处罚后,行人闯红灯的概率,结合试行对闯红灯的行人进行经济处罚前的概率,可得出结论;
(3)结合表格中的数据,可针对45岁以上人群开展“道路安全”宣传教育;也可进行适当的经济处罚,得到相应的结论.
【解答】解:(1)2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 15 25 40
未闯红灯人数 85 75 160
合计 100 100 200
因为
所以有90%的把握认为闯红灯行为与年龄有关.
(2)在试行对闯红灯的行人进行经济处罚后,行人闯红灯的概率为,
而在试行对闯红灯的行人进行经济处罚前,行人闯红灯的概率为0.2,
故在试行对闯红灯的行人进行经济处罚后,闯红灯现象有明显改善.
(3)①根据调查数据显示,行人闯红灯与年龄有明显关系,故可以针对45岁以上人群开展“道路安全”宣传教育;
②由于经济处罚可以明显降低行人闯红灯的概率,故可以在法律允许范围内进行适当的经济处罚.
【点评】本题考查独立性检验,属于基础题.
18.红旗中学高三年级共有学生1800名,在一次数学考试后,抽取了200名同学的成绩(满分150分),绘制成频率分布直方图(如图),成绩的分组区间为[60,70),[70,80),[80,90),…,[140,150].
(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)由样本估计总体、估计这次考试,年级成绩优秀(分数大于或等于120分即为优秀)人数和平均分数(用各组的中点值代替该组的平均值).
【分析】(Ⅰ)根据频率之和为1即可求解;
(Ⅱ)求出样本中分数大于或等于120分的频率,从而求出人数,再根据平均数公式即可求解.
【解答】解:(Ⅰ)由题意,得(0.0010+0.0050+0.0100+a+0.0190+0.0250+a+0.0075+0.0025)×10=1,解得a=0.0150;
(Ⅱ)由频率分布直方图,得样本中,分数大于或等于120分的频率为(0.0150+0.0075+0.0025)×10=0.25,
由样本估计总体,得高三年级这次数学考试成绩的优秀率为25%,
这次考试年级优秀人数为1800×25%=450,
设样本的平均分数为,
=(65×0.0010+75×0.0050+85×0.0100+95×0.0150+105×0.0190+115×0.0250+125×0.0150+135×0.0075+145×0.0025)×10=108.35,
由样本估计总体,估计这次考试平均分数为108.35分,
这次数学考试,估计优秀人数有450人,平均分数为108.35分.
【点评】本题考查频率分布直方图的应用,属于基础题.
19.网络直播带货助力乡村振兴,它作为一种新颖的销售土特产的方式,受到社会各界的追捧.某直播间开展地标优品带货直播活动,其主播直播周期次数x(其中10场为一个周期)与产品销售额y(千元)的数据统计如下:
直播周期数x 1 2 3 4 5
产品销售额y(千元) 3 7 15 30 40
根据数据特点,甲认为样本点分布在指数型曲线y=2bx+a的周围,据此他对数据进行了一些初步处理.如下表:
3.7 55 382 65 978 101
其中zi=log2yi,=
(1)请根据表中数据,建立y关于x的回归方程(系数精确到0.01);
(2)①乙认为样本点分布在直线y=mx+n的周围,并计算得回归方程为=9.7x﹣10.1,以及该回归模型的相关指数R乙2=0.98,试比较甲、乙两人所建立的模型,谁的拟合效果更好?
②由①所得的结论,计算该直播间欲使产品销售额达到8万元以上,直播周期数至少为多少?(最终答案精确到1)
附:对于一组数据 (u1,v1)(u2,v2),…,(un,vn),其回归直线=+u的斜率和截距的最小二乘估计分别为=,=,相关系数:R2=1﹣.
【分析】(1)对y=2bx+a两边取对数,得log2y=bx+a,设z=log2y,有z=bx+a,根据已知数据求出z关于x的回归方程,即可得y关于x的回归方程;
(2)①计算可得R甲2≈0.90<0.98,再由相关系数越大,拟合效果越好,得解;
②令=9.7x﹣10.1>8,求出x的范围,即可.
【解答】解:(1)对y=2bx+a两边取对数,得log2y=(bx+a)log22=bx+a,
设z=log2y,则z=bx+a,
由表中数据可知,=×(1+2+3+4+5)=3,
所以===0.95,=﹣=3.7﹣0.95×3=0.85,
所以=0.95x+0.85,
所以log2y=0.95x+0.85,即y=20.95x+0.85,
故y关于x的回归方程为y=20.95x+0.85.
(2)①R甲2=1﹣=1﹣≈0.90<0.98,
所以乙建立的模型拟合效果更好.
②令=9.7x﹣10.1>8,解得x>≈1.9,
故该直播间欲使产品销售额达到8万元以上,直播周期数至少为2次.
【点评】本题考查回归方程的求法与应用,相关系数的含义,考查逻辑推理能力和运算能力,属于中档题.
20.据统计,某校高三打印室1﹣4月份购买的打印纸的箱数如表:
月份代号t 1 2 3 4
打印纸的数量y(箱) 60 65 70 85
(1)求相关系数r,并从r的角度分析能否用线性回归模型拟合y与t的关系(若|r|≥0.75,则线性相关程度很强,可用线性回归模型拟合);
(2)建立y关于t的回归方程,并用其预测5月份该校高三打印室需购买的打印纸约为多少箱.
参考公式:对于一组具有线性相关关系的数据(xi,yi)(i=1,2,3, ,n),其回归直线的斜率和截距的最小二乘估计分别为=,.
相关系数,参考数据:
【分析】(1)利用相关系数公式结合条件即得;
(2)根据最小二乘法可得线性回归直线方程,然后将t=5代入回归方程即得.
【解答】解:(1)由已知数据可得=,
又852=19950,,
所以===,
因为r>0.75,所以线性相关程度很强,可用线性回归模型拟合y与t的关系;
(2)因为b====8,,
所以y关于t的回归方程为y=8t+50,
将t=5代入回归方程,得箱,
所以预测5月份该校高三打印室需购买的打印纸约为90箱.
【点评】本题主要考查了相关系数的计算,考查了线性回归方程的应用,属于中档题.
21.中国男篮历史上曾12次参加亚运会,其中8次夺得金牌,是亚运会夺冠次数最多的球队.第19届亚运会将于2023年9月23日至10月8日在杭州举办.
(1)为了解喜爱篮球运动是否与性别有关,某学校随机抽取了男生和女生各100名进行调查,得到2×2列联表如下:
喜爱篮球 不喜爱篮球合计
男生 65 35 100
女生 25 75 100
合计 90 110 200
依据小概率值α=0.001的独立性检验,能否认为喜爱篮球运动与性别有关?
(2)校篮球队中的甲、乙、丙三名球员将进行传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,第n次触球者是甲的概率记为Pn,即P1=1.
(i)求P3,P4,并证明:为等比数列;
(ii)比较第15次触球者是甲与第15次触球者是乙的概率的大小.
参考公式:,其中n=a+b+c+d为样本容量.
参考数据:
P(K2≥k) 0.10 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
【分析】(1)假设H0:喜爱足球运动与性别独立,即喜爱足球运动与性别无关,计算K2,对照附表即可得出结论.
(2)(i)根据题意写出P3、P4的值,第n次触球者是甲的概率记为Pn,n≥2时,第n﹣1次触球者是甲的概率为Pn﹣1,第n﹣1次触球者不是甲的概率为1﹣Pn﹣1,由此得出Pn﹣=﹣(Pn﹣1﹣),即可判断{Pn﹣}是等比数列;
(ii)写出Pn,计算P15和Q15=(1﹣P15)的值,比较大小即可.
【解答】解:(1)假设H0:喜爱足球运动与性别独立,即喜爱足球运动与性别无关,
计算K2=≈32.323>10.828,
根据小概率值α=0.001的独立性检验,我们推断H0不成立,
即认为喜爱足球运动与性别有关,此推断犯错误的概率不超过0.001.
(2)(i)由题意知,P1=1,P2=0,P3=,P4=×0+(1﹣)×=;
证明:第n次触球者是甲的概率记为Pn,
则当n≥2时,第n﹣1次触球者是甲的概率为Pn﹣1,
第n﹣1次触球者不是甲的概率为1﹣Pn﹣1,
则Pn=Pn﹣1×0+(1﹣Pn﹣1)×=(1﹣Pn﹣1),
从而Pn﹣=﹣(Pn﹣1﹣),
又P1﹣=,
所以{Pn﹣}是以为首项,公比为﹣的等比数列,
(ii)第n次触球者是甲的概率为Pn=×+,
所以P15=×+=×+>,
第15次触球者是乙的概率为Q15=(1﹣P15)=(1﹣×﹣)=﹣×<,
所以第15次触球者是甲的概率比第15次触球者是乙的概率大.
【点评】本题考查了列联表与独立性检验应用问题,也考查了概率与统计的应用问题,是难题.
22.2022年11月17日,由工业和信息化部、安徽省人民政府共同主办的第十七届“中国芯”集成电路产业大会在合肥成功举办.此次大会以“强芯固基以质为本”为主题,旨在培育壮大我国集成电路产业,夯实产业基础、营造良好产业生态.2022年,全国芯片研发单位相比2006年增加194家,提交芯片数量增加299个,均增长超过6倍.某芯片研发单位用在“A芯片”上研发费用占本单位总研发费用的百分比y(%)如表所示.
年份 2016 2017 2018 2019 2020 2021 2022
年份代码 1 2 3 4 5 6 7
y 20% 30% 32% 39% 42% 46% 50%
(1)根据表中的数据,作出相应的折线图;并结合相关数据,计算相关系数r,并推断y与t线性相关程度;(已知:0.8≤|r|≤1,则认为y与t线性相关很强;0.3≤|r|<0.8,则认为y与t线性相关一般;|r|<0.3,则认为y与t线性相关较弱)
(2)求出y与t的回归直线方程(保留一位小数);
(3)请判断,若2024年用在“A芯片”上研发费用不低于295万元,则该单位2024年芯片研发的总费用预算为500万元是否符合研发要求?
附:相关数据:,,,.
相关计算公式:①相关系数;
在回归直线方程中,,.
【分析】(1)根据表格数据可绘制折线图,结合公式可求得相关系数r,对比已知线性相关强度判断依据即可得到结论;
(2)采用最小二乘法即可求得回归直线;
(3)将t=9代入回归直线可求得,进而计算得到预算为500万元时的研发费用的预估值,由此可得结论.
【解答】解:(1)折线图如下:
由题意得:,∴,∴,
∴,
∵|0.98|>0.8,∴y与t线性相关很强;
(2)由题意得:,∴,
∴y关于t的回归直线方程为;
(3)2024年对应的年份代码t=9,则当t=9时,,
∴预测2024年用在“A芯片”上的研发费用约为500×60.5%=302.5(万元),
∵302.5>295,∴符合研发要求.
【点评】本题主要考查了利用最小二乘法求回归直线方程,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2023年高中数学统计套题
一.选择题(共8小题)
1.空气质量指数是评估空气质量状况的一组数字,空气质量指数划分为[0,50)、[50,100)、[100,150)、[150,200)、[200,300)和[300,500]六档,分别对应“优”、“良”、“轻度污染”、“中度污染”、“重度污染”和“严重污染”六个等级.如图是某市2月1日至14日连续14天的空气质量指数趋势图,则下面说法中正确的是( )
A.这14天中有5天空气质量为“中度污染”
B.从2日到5日空气质量越来越好
C.这14天中空气质量指数的中位数是214
D.连续三天中空气质量指数方差最小是5日到7日
2.甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(图1),茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(图2)完好,则( )
A.甲的单场平均得分比乙低
B.乙的60%分位数为19
C.甲、乙的极差均为11
D.乙得分的中位数是16.5
3.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;方差分别为,则下面正确的是( )
A. B.
C. D.
4.某市质量检测部门从辖区内甲、乙两个地区的食品生产企业中分别随机抽取9家企业,根据食品安全管理考核指标对抽到的企业进行考核,并将各企业考核得分整理成如下的茎叶图.由茎叶图所给信息,可判断以下结论中正确是( )
A.若a=2,则甲地区考核得分的极差大于乙地区考核得分的极差
B.若a=4,则甲地区考核得分的平均数小于乙地区考核得分的平均数
C.若a=5,则甲地区考核得分的方差小于乙地区考核得分的方差
D.若a=6,则甲地区考核得分的中位数小于乙地区考核得分的中位数
5.关于统计数据的分析,有以下几个结论,其中正确的是( )
A.将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化
B.样本数据9、3、5、7、12、13、1、8、10、18的中位数是8或9
C.在刻画回归模型的拟合效果时,相关指数R2的值越大,说明拟合的效果越好
D.在调查影院中观众观后感时,从20排中(每排人数相同)每排任意抽取一人进行调查是系统抽样法
6.根据变量x与y的对应关系(如表),求得y关于x的线性回归方程为y=6.5x+17.5,则表中m的值为( )
x 2 4 5 6 8
y 30 40 m 50 70
A.60 B.55 C.50 D.45
7.已知变量的关系可以用模型y=kemx拟合,设z=lny,其变换后得到一组数据如下.由表可得线性回归方程z=3x+a,则k=( )
x 1 2 3 4 5
z 2 4 5 10 14
A.e﹣3 B.e﹣2 C.e2 D.e3
8.关于线性回归的描述,下列说法不正确的是( )
A.回归直线方程中变量x,y成正相关关系
B.相关系数r越接近1,相关程度越强
C.回归直线方程中变量x,y成正相关关系
D.残差平方和越小,拟合效果越好
二.多选题(共4小题)
(多选)9.给定数5,4,3,5,3,2,2,3,1,2,则这组数据的( )
A.中位数为3 B.方差为
C.众数为3 D.85%分位数为4.5
(多选)10.树人中学2006班某科研小组,持续跟踪调查了他们班全体同学一学期中16周锻炼身体的时长,经过整理得到男生、女生各周锻炼身体的平均时长(单位:h)的数据如下:
男生:6.3、7.4、7.6、8.1、8.2、8.2、8.5、8.6、8.6、8.6、8.6、9.0、9.2、9.3、9.8、10.1;
女生:5.1、5.6、6.0、6.3、6.5、6.8、7.2、7.3、7.5、7.7、8.1、8.2、8.4、8.6、9.2、9.4.
以下判断中正确的是( )
A.女生每周锻炼身体的平均时长的平均值等于8
B.男生每周锻炼身体的平均时长的80%分位数是9.2
C.男生每周锻炼身体的平均时长大于9h的概率的估计值为0.3125
D.与男生相比,女生每周锻炼身体的平均时长波动性比较大
(多选)11.下列关于成对数据的统计说法正确的有( )
A.若当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关
B.样本相关系数r的绝对值大小可以反映成对样本数据之间线性相关的程度
C.通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据
D.决定系数R2越大,模型的拟合效果越差
(多选)12.某校抽取了某班20名学生的化学成绩,并将他们的成绩制成如下所示的表格.
成绩 60 65 70 75 80 85 90
人数 2 3 3 5 4 2 1
下列结论正确的是( )
A.这20人成绩的众数为75
B.这20人成绩的极差为30
C.这20人成绩的25%分位数为65
D.这20人成绩的平均数为75
三.填空题(共4小题)
13.某高中的三个年级共有学生2000人,其中高一600人,高二680人,高三720人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 .
14.某班共有50名学生,在期末考试中,小明因病未参加数学考试.参加考试的49名学生的数学成绩的方差为2.在评估数学成绩时,老师把小明的数学成绩按这49名学生的数学成绩的平均数来算,那么全班50名学生的数学成绩的标准差为 .
15.设一组样本数据x1,x2,…,x8的方差为6,则数据3x1+1,3x2+1,…,3x8+1的方差是 .
16.身体质量指数,也就是BMI指数,简称体质指数,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.某校为了解该校学生的身体健康情况,从某班随机抽取20名学生进行调查,得到这20名学生的BMI指数分别是15,15.3,15.6,15.9,16.2,16.6,17.5,17.8,18.2,18.7,19.3,19.5,20.3,21.1,21.5,22.7,22.9,23.1,23.4,23.5,则这组数据的第65百分位数是 .
四.解答题(共6小题)
17.某市从2020年5月1日开始,若电子警察抓拍到机动车不礼让行人的情况后,交警部门将会对不礼让行人的驾驶员进行扣3分,罚款200元的处罚,并在媒体上曝光.但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患和机动车通畅率降低的情况.交警部门在某十字路口根据以往的监测数据,得到行人闯红灯的概率为0.2,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯的情况进行统计,得到2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 25
未闯红灯数 85
合计 200
近期,为了整顿“行人闯红灯”这一不文明的违法行为,交警部门在该十字路口试行了对闯红灯的行人进行5元以上,50元以下的经济处罚.在试行经济处罚一段时间后,交警部门再次对穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯的情况进行统计,得到2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 5 15 20
未闯红灯人数 95 85 180
合计 100 100 200
将统计数据所得频率视为概率,完成下列问题:
(1)将2×2列联表填写完整(不需要写出填写过程),并根据表中数据分析,在试行对闯红灯的行人进行经济处罚前,是否有90%的把握认为闯红灯行为与年龄有关;
(2)在试行对闯红灯的行人进行经济处罚后,闯红灯现象是否有明显改善,请说明理由;
(3)结合调查结果,请你对“如何治理行人闯红灯现象”提出合理的建议(至少提出两条建议).
18.红旗中学高三年级共有学生1800名,在一次数学考试后,抽取了200名同学的成绩(满分150分),绘制成频率分布直方图(如图),成绩的分组区间为[60,70),[70,80),[80,90),…,[140,150].
(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)由样本估计总体、估计这次考试,年级成绩优秀(分数大于或等于120分即为优秀)人数和平均分数(用各组的中点值代替该组的平均值).
19.网络直播带货助力乡村振兴,它作为一种新颖的销售土特产的方式,受到社会各界的追捧.某直播间开展地标优品带货直播活动,其主播直播周期次数x(其中10场为一个周期)与产品销售额y(千元)的数据统计如下:
直播周期数x 1 2 3 4 5
产品销售额y(千元) 3 7 15 30 40
根据数据特点,甲认为样本点分布在指数型曲线y=2bx+a的周围,据此他对数据进行了一些初步处理.如下表:
3.7 55 382 65 978 101
其中zi=log2yi,=
(1)请根据表中数据,建立y关于x的回归方程(系数精确到0.01);
(2)①乙认为样本点分布在直线y=mx+n的周围,并计算得回归方程为=9.7x﹣10.1,以及该回归模型的相关指数R乙2=0.98,试比较甲、乙两人所建立的模型,谁的拟合效果更好?
②由①所得的结论,计算该直播间欲使产品销售额达到8万元以上,直播周期数至少为多少?(最终答案精确到1)
附:对于一组数据 (u1,v1)(u2,v2),…,(un,vn),其回归直线=+u的斜率和截距的最小二乘估计分别为=,=,相关系数:R2=1﹣.
20.据统计,某校高三打印室1﹣4月份购买的打印纸的箱数如表:
月份代号t 1 2 3 4
打印纸的数量y(箱) 60 65 70 85
(1)求相关系数r,并从r的角度分析能否用线性回归模型拟合y与t的关系(若|r|≥0.75,则线性相关程度很强,可用线性回归模型拟合);
(2)建立y关于t的回归方程,并用其预测5月份该校高三打印室需购买的打印纸约为多少箱.
参考公式:对于一组具有线性相关关系的数据(xi,yi)(i=1,2,3, ,n),其回归直线的斜率和截距的最小二乘估计分别为=,.
相关系数,参考数据:
21.中国男篮历史上曾12次参加亚运会,其中8次夺得金牌,是亚运会夺冠次数最多的球队.第19届亚运会将于2023年9月23日至10月8日在杭州举办.
(1)为了解喜爱篮球运动是否与性别有关,某学校随机抽取了男生和女生各100名进行调查,得到2×2列联表如下:
喜爱篮球 不喜爱篮球合计
男生 65 35 100
女生 25 75 100
合计 90 110 200
依据小概率值α=0.001的独立性检验,能否认为喜爱篮球运动与性别有关?
(2)校篮球队中的甲、乙、丙三名球员将进行传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,第n次触球者是甲的概率记为Pn,即P1=1.
(i)求P3,P4,并证明:为等比数列;
(ii)比较第15次触球者是甲与第15次触球者是乙的概率的大小.
参考公式:,其中n=a+b+c+d为样本容量.
参考数据:
P(K2≥k) 0.10 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
22.2022年11月17日,由工业和信息化部、安徽省人民政府共同主办的第十七届“中国芯”集成电路产业大会在合肥成功举办.此次大会以“强芯固基以质为本”为主题,旨在培育壮大我国集成电路产业,夯实产业基础、营造良好产业生态.2022年,全国芯片研发单位相比2006年增加194家,提交芯片数量增加299个,均增长超过6倍.某芯片研发单位用在“A芯片”上研发费用占本单位总研发费用的百分比y(%)如表所示.
年份 2016 2017 2018 2019 2020 2021 2022
年份代码 1 2 3 4 5 6 7
y 20% 30% 32% 39% 42% 46% 50%
(1)根据表中的数据,作出相应的折线图;并结合相关数据,计算相关系数r,并推断y与t线性相关程度;(已知:0.8≤|r|≤1,则认为y与t线性相关很强;0.3≤|r|<0.8,则认为y与t线性相关一般;|r|<0.3,则认为y与t线性相关较弱)
(2)求出y与t的回归直线方程(保留一位小数);
(3)请判断,若2024年用在“A芯片”上研发费用不低于295万元,则该单位2024年芯片研发的总费用预算为500万元是否符合研发要求?
附:相关数据:,,,.
相关计算公式:①相关系数;
在回归直线方程中,,.
2023年高中数学统计套题
参考答案与试题解析
一.选择题(共8小题)
1.空气质量指数是评估空气质量状况的一组数字,空气质量指数划分为[0,50)、[50,100)、[100,150)、[150,200)、[200,300)和[300,500]六档,分别对应“优”、“良”、“轻度污染”、“中度污染”、“重度污染”和“严重污染”六个等级.如图是某市2月1日至14日连续14天的空气质量指数趋势图,则下面说法中正确的是( )
A.这14天中有5天空气质量为“中度污染”
B.从2日到5日空气质量越来越好
C.这14天中空气质量指数的中位数是214
D.连续三天中空气质量指数方差最小是5日到7日
【分析】根据题意,由折线图分析数据,由此分析选项是否正确,即可得答案.
【解答】解:根据题意,依次分析选项:
对于A,这14天中有4天空气质量指数在[150,200)之间,则有4天为“中度污染”,A错误;
对于B,从2日到5日空气质量逐渐下降,即空气质量越来越好,B正确;
对于C,将14组数据从小到大排列:80,83,138,155,157,165,179,214,214,221,243,260,263,275,其中位数为(179+214)=196.5,C错误;
对于D,5日到7日的三天,数据相差比较大,则连续三天中空气质量指数方差最小不是5日到7日,D错误.
故选:B.
【点评】本题考查由折线图分析数据,涉及中位数、方差的意义,属于基础题.
2.甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(图1),茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(图2)完好,则( )
A.甲的单场平均得分比乙低
B.乙的60%分位数为19
C.甲、乙的极差均为11
D.乙得分的中位数是16.5
【分析】根据茎叶图、折线图,平均数、中位数、百分数、极差的求法判断各项的正误即可.
【解答】解:A:由茎叶图和折线图,甲比赛得分为{9,12,13,14,15,20,26,28},平均得分为,
乙比赛得分为{9,14,15,16,17,18,19,20},平均得分为,甲高于乙,故A错误;
B:由8×60%=4.8,故乙的60%分位数为17,故B错误;
C:甲的极差为28﹣9=19,乙的极差为20﹣9=11,故C错误;
D:乙得分的中位数是,故D正确.
故选:D.
【点评】本题主要考查了茎叶图的应用,考查了平均数、百分位数、中位数和极差的计算,属于基础题.
3.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;方差分别为,则下面正确的是( )
A. B.
C. D.
【分析】根据直方图求出甲、乙地区用户满意度评分的中位数,并通过两地区用户满意度评分的集中程度即可得到哪个方差小.
【解答】解:由频率分布直方图得:
甲地区:[40,60)的频率为(0.015+0.020)×10=0.35,[60,70)的频率为0.025×10=0.25,
∴甲地区用户满意度评分的中位数,
乙地区:[50,70)的频率为(0.005+0.020)×10=0.25,[70,80)的频率为0.035×10=0.35,
∴乙地区用户满意度评分的中位数,
∴m1<m2,
由直方图可以看出,乙地区用户满意度评分的集中程度比甲地区的高,
∴.
故选:D.
【点评】本题主要考查了频率分布直方图的应用,考查了中位数和方差的计算,属于基础题.
4.某市质量检测部门从辖区内甲、乙两个地区的食品生产企业中分别随机抽取9家企业,根据食品安全管理考核指标对抽到的企业进行考核,并将各企业考核得分整理成如下的茎叶图.由茎叶图所给信息,可判断以下结论中正确是( )
A.若a=2,则甲地区考核得分的极差大于乙地区考核得分的极差
B.若a=4,则甲地区考核得分的平均数小于乙地区考核得分的平均数
C.若a=5,则甲地区考核得分的方差小于乙地区考核得分的方差
D.若a=6,则甲地区考核得分的中位数小于乙地区考核得分的中位数
【分析】根据极差、平均数、中位数的计算方法判断ABD;由波动程度判断C.
【解答】解:对于选项A:甲地区考核得分的极差为94﹣75=19,乙地区考核得分的极差为99﹣74=25,
即甲地区考核得分的极差小于乙地区考核得分的极差,故选项A错误;
对于选项B:甲地区考核得分的平均数为,
乙地区考核得分的平均数为,
即甲地区考核得分的平均数大于乙地区考核得分的平均数,故选项B错误;
对于选项C:甲地区考核得分从小到大排列为:75,78,81,84,85,88,92,93,94,
乙地区考核得分从小到大排列为:74,77,80,83,84,87,91,95,99,
由以上数据可知,乙地区考核得分的波动程度比甲地区考核得分的波动程度大,即甲地区考核得分的方差小于乙地区考核得分的方差,故选项C正确;
对于选项D:由茎叶图可知,甲地区考核得分的中位数为85,乙地区考核得分的中位数为84,即甲地区考核得分的中位数大于乙地区考核得分的中位数,故选项D错误;
故选:C.
【点评】本题主要考查了茎叶图的应用,考查了极差、平均数、中位数的计算,属于基础题.
5.关于统计数据的分析,有以下几个结论,其中正确的是( )
A.将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化
B.样本数据9、3、5、7、12、13、1、8、10、18的中位数是8或9
C.在刻画回归模型的拟合效果时,相关指数R2的值越大,说明拟合的效果越好
D.在调查影院中观众观后感时,从20排中(每排人数相同)每排任意抽取一人进行调查是系统抽样法
【分析】根据平均数与方差、中位数和线性相关系数,以及抽样方法的定义,对选项的问题分析与判断即可.
【解答】解:对于A,将一组数据中的每个数据都减去同一个数后,平均数减小,方差不变,所以选项A错误;
对于B,样本数据按从小到大顺序排列为1、3、5、7、8、9、10、12、13、18,所以中位数是=8.5,选项B错误;
对于C,刻画回归模型的拟合效果时,相关指数R2的值越大,说明拟合的效果越好,选项C正确;
对于D,调查影院中观众观后感时,从20排中(每排人数相同)每排任意抽取一人进行调查是简单随机抽样,不是系统抽样法,选项D错误;
故选:C.
【点评】本题考查了对平均数与方差、中位数和线性相关系数,以及抽样方法的理解与判断问题,是基础题.
6.根据变量x与y的对应关系(如表),求得y关于x的线性回归方程为y=6.5x+17.5,则表中m的值为( )
x 2 4 5 6 8
y 30 40 m 50 70
A.60 B.55 C.50 D.45
【分析】先求得样本点中心,再根据回归直线过样本点中心即可求解.
【解答】解:由表中数据,计算,,
因为回归直线方程过样本中心,
∴,
解得m=60.
故选:A.
【点评】本题考查线性回归方程的运用,解题的关键是利用线性回归方程恒过样本中心点,这是线性回归方程中最常考的知识点.属于基础题.
7.已知变量的关系可以用模型y=kemx拟合,设z=lny,其变换后得到一组数据如下.由表可得线性回归方程z=3x+a,则k=( )
x 1 2 3 4 5
z 2 4 5 10 14
A.e﹣3 B.e﹣2 C.e2 D.e3
【分析】根据样本中心点在回归方程上可得a=﹣2,再利用对数运算法则即可得lnk+mx=3x﹣2,所以k=e﹣2.
【解答】解:由表格数据知,.即样本中心点为(3,7),
由z=3x+a,得a=7﹣3×3=﹣2,
即z=3x﹣2,
所以z=lny=lnk+mx=3x﹣2,即lnk=﹣2,可得k=e﹣2,
故选:B.
【点评】本题考查线性回归方程的运用,解题的关键是利用线性回归方程恒过样本中心点,这是线性回归方程中最常考的知识点.属于基础题.
8.关于线性回归的描述,下列说法不正确的是( )
A.回归直线方程中变量x,y成正相关关系
B.相关系数r越接近1,相关程度越强
C.回归直线方程中变量x,y成正相关关系
D.残差平方和越小,拟合效果越好
【分析】根据线性回归的性质可知:b的正负决定正负相关,可判断选项A,C;根据相关系数的绝对值越接近1,相关性越强,可判断B;残差平方和越小,拟合效果越好,可判断选项D.
【解答】解:对于A,因为回归直线方程中的b<0,所以变量x,y成负相关关系,故选项A错误;
对于B,因为相关系数r的绝对值越接近1,相关度越强,所以当相关系数r越接近1,相关程度越强,故选项B正确;
对于C,因为回归直线方程中的b=1.1>0,所以变量x,y成正相关关系,故选项C正确;
对于D,因为残差平方和越小,拟合效果越好,所以选项D正确,
综上:说法不正确的是A,
故选:A.
【点评】本题主要考查了线性回归方程的应用,属于基础题.
二.多选题(共4小题)
(多选)9.给定数5,4,3,5,3,2,2,3,1,2,则这组数据的( )
A.中位数为3 B.方差为
C.众数为3 D.85%分位数为4.5
【分析】先将数5,4,3,5,3,2,2,3,1,2,按小到大的顺序排列,再逐项判断.
【解答】解:将数5,4,3,5,3,2,2,3,1,2,按小到大的顺序排列为:1,2,2,2,3,3,3,4,5,5,
则这组数据的中位数为,故A正确;
数据中2,3,出现的次数最多,所以众数为2和3,故C错误;
平均数为:,
则方差为,故B正确;
第85%分位数是数据中至少有85%的数据小于或等于该数,因此,从小到大第9个数字为5,故D错误,
故选:AB.
【点评】本题主要考查了中位数,平均数和方差的计算,属于基础题.
(多选)10.树人中学2006班某科研小组,持续跟踪调查了他们班全体同学一学期中16周锻炼身体的时长,经过整理得到男生、女生各周锻炼身体的平均时长(单位:h)的数据如下:
男生:6.3、7.4、7.6、8.1、8.2、8.2、8.5、8.6、8.6、8.6、8.6、9.0、9.2、9.3、9.8、10.1;
女生:5.1、5.6、6.0、6.3、6.5、6.8、7.2、7.3、7.5、7.7、8.1、8.2、8.4、8.6、9.2、9.4.
以下判断中正确的是( )
A.女生每周锻炼身体的平均时长的平均值等于8
B.男生每周锻炼身体的平均时长的80%分位数是9.2
C.男生每周锻炼身体的平均时长大于9h的概率的估计值为0.3125
D.与男生相比,女生每周锻炼身体的平均时长波动性比较大
【分析】根据平均数公式可判断A选项;利用百分位数的定义可判断B选项;利用频率估计概率可判断C选项;利用极差与男生、女生锻炼的平均时长的分布可判断D选项.
【解答】解:对于A选项,由平均数公式可知,
女生每周锻炼身体的平均时长的平均值等于=7.36875(h),A错;
对于B选项,因为16×0.8=12.8,
因此,男生每周锻炼身体的平均时长的80%分位数是9.2h,B对;
对于C选项,男生每周锻炼身体的平均时长大于9h的有4周,
所求概率为,C错;
对于D选项,男生每周锻炼身体的平均时长分布在区间(8,9)内共有8个,女生有4个,
男生每周锻炼身体的平均时长分布在区间(7,10)内的共14个,女生为10个,
男生每周锻炼身体的平均时长的极差为10.1﹣6.3=3.8,女生为9.4﹣5.1=4.3,
据此可知与男生相比,女生每周锻炼身体的平均时长波动性比较大,
所以,与男生相比,女生每周锻炼身体的平均时长波动性比较大,D对.
故选:BD.
【点评】本题主要考查了平均数、极差的计算,考查了古典概型的概率公式,属于中档题.
(多选)11.下列关于成对数据的统计说法正确的有( )
A.若当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关
B.样本相关系数r的绝对值大小可以反映成对样本数据之间线性相关的程度
C.通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据
D.决定系数R2越大,模型的拟合效果越差
【分析】根据题意,由变量间相关关系的定义依次分析选项是否正确,即可得答案.
【解答】解:根据题意,依次分析选项:
对于A,由变量相关的定义,可得A正确;
对于B,样本相关系数r的绝对值越大,样本数据之间线性相关的程度越高,则样本相关系数r的绝对值大小可以反映成对样本数据之间线性相关的程度,B正确;
对于C,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据,C正确;
对于D,系数R2越大,模型的拟合效果越好,D错误.
故选:ABC.
【点评】本题考查变量间的相关关系,涉及回归分析的基本概念,属于基础题.
(多选)12.某校抽取了某班20名学生的化学成绩,并将他们的成绩制成如下所示的表格.
成绩 60 65 70 75 80 85 90
人数 2 3 3 5 4 2 1
下列结论正确的是( )
A.这20人成绩的众数为75
B.这20人成绩的极差为30
C.这20人成绩的25%分位数为65
D.这20人成绩的平均数为75
【分析】根据众数的概念,极差的概念,百分位数的概念,平均数的概念,即可分别求解.
【解答】解:对A选项,∵这20名学生的化学成绩的众数为75,∴A正确;
对B选项,∵这20名学生的化学成绩的极差为90﹣60=30,∴B正确;
对C选项,∵20×25%=5,∴这20人成绩的25%分位数为=67.5,∴C错误;
对D选项,∵这20名学生的化学成绩的平均数为:
=74,∴D错误.
故选:AB.
【点评】本题考众数的概念,极差的概念,百分位数的概念,平均数的概念,属基础题.
三.填空题(共4小题)
13.某高中的三个年级共有学生2000人,其中高一600人,高二680人,高三720人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 15 .
【分析】根据分层抽样原则直接计算即可.
【解答】解:由题意,从全校2000人中抽取50人访谈,按照年级分层,则高一年级应该抽人.
故答案为:15.
【点评】本题主要考查了分层抽样的定义,属于基础题.
14.某班共有50名学生,在期末考试中,小明因病未参加数学考试.参加考试的49名学生的数学成绩的方差为2.在评估数学成绩时,老师把小明的数学成绩按这49名学生的数学成绩的平均数来算,那么全班50名学生的数学成绩的标准差为 .
【分析】先由题意得到,再由数学成绩的标准差为求解.
【解答】解:设参加考试的49名学生的数学成绩为xi(i=1,2,3,...,49),平均成绩为,
由题意得,
则全班50名学生的数学成绩的标准差为:,=,=.
故答案为:.
【点评】本题主要考查了数据标准差的计算,属于基础题.
15.设一组样本数据x1,x2,…,x8的方差为6,则数据3x1+1,3x2+1,…,3x8+1的方差是 54 .
【分析】设x1,x2, ,x8的平均数为,结合x1,x2, ,x8的方差为6,根据平均数和方差的计算公式得到3x1+1,3x2+1, ,3x8+1的平均数和方差.
【解答】解:设x1,x2, ,x8的平均数为,
则x1+x2+…+x8=8,
又,
故3x1+1,3x2+1, ,3x8+1的平均数为,
方差为=.
故答案为:54.
【点评】本题主要考查了方差公式及方差性质的应用,属于基础题.
16.身体质量指数,也就是BMI指数,简称体质指数,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.某校为了解该校学生的身体健康情况,从某班随机抽取20名学生进行调查,得到这20名学生的BMI指数分别是15,15.3,15.6,15.9,16.2,16.6,17.5,17.8,18.2,18.7,19.3,19.5,20.3,21.1,21.5,22.7,22.9,23.1,23.4,23.5,则这组数据的第65百分位数是 20.7 .
【分析】根据百分位数的定义即可求解.
【解答】解:因为20×0.65=13,
所以这组数据的第65百分位数是.
故答案为:20.7.
【点评】本题主要考查百分数的定义,属于基础题.
四.解答题(共6小题)
17.某市从2020年5月1日开始,若电子警察抓拍到机动车不礼让行人的情况后,交警部门将会对不礼让行人的驾驶员进行扣3分,罚款200元的处罚,并在媒体上曝光.但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患和机动车通畅率降低的情况.交警部门在某十字路口根据以往的监测数据,得到行人闯红灯的概率为0.2,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯的情况进行统计,得到2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 25
未闯红灯数 85
合计 200
近期,为了整顿“行人闯红灯”这一不文明的违法行为,交警部门在该十字路口试行了对闯红灯的行人进行5元以上,50元以下的经济处罚.在试行经济处罚一段时间后,交警部门再次对穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯的情况进行统计,得到2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 5 15 20
未闯红灯人数 95 85 180
合计 100 100 200
将统计数据所得频率视为概率,完成下列问题:
(1)将2×2列联表填写完整(不需要写出填写过程),并根据表中数据分析,在试行对闯红灯的行人进行经济处罚前,是否有90%的把握认为闯红灯行为与年龄有关;
(2)在试行对闯红灯的行人进行经济处罚后,闯红灯现象是否有明显改善,请说明理由;
(3)结合调查结果,请你对“如何治理行人闯红灯现象”提出合理的建议(至少提出两条建议).
【分析】(1)根据题意,填写出2×2列联表,利用公式求得K2的值,结合附表,即可得到结论;
(2)求得试行对闯红灯的行人进行经济处罚后,行人闯红灯的概率,结合试行对闯红灯的行人进行经济处罚前的概率,可得出结论;
(3)结合表格中的数据,可针对45岁以上人群开展“道路安全”宣传教育;也可进行适当的经济处罚,得到相应的结论.
【解答】解:(1)2×2列联表如下:
45岁以下 45岁以上 合计
闯红灯人数 15 25 40
未闯红灯人数 85 75 160
合计 100 100 200
因为
所以有90%的把握认为闯红灯行为与年龄有关.
(2)在试行对闯红灯的行人进行经济处罚后,行人闯红灯的概率为,
而在试行对闯红灯的行人进行经济处罚前,行人闯红灯的概率为0.2,
故在试行对闯红灯的行人进行经济处罚后,闯红灯现象有明显改善.
(3)①根据调查数据显示,行人闯红灯与年龄有明显关系,故可以针对45岁以上人群开展“道路安全”宣传教育;
②由于经济处罚可以明显降低行人闯红灯的概率,故可以在法律允许范围内进行适当的经济处罚.
【点评】本题考查独立性检验,属于基础题.
18.红旗中学高三年级共有学生1800名,在一次数学考试后,抽取了200名同学的成绩(满分150分),绘制成频率分布直方图(如图),成绩的分组区间为[60,70),[70,80),[80,90),…,[140,150].
(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)由样本估计总体、估计这次考试,年级成绩优秀(分数大于或等于120分即为优秀)人数和平均分数(用各组的中点值代替该组的平均值).
【分析】(Ⅰ)根据频率之和为1即可求解;
(Ⅱ)求出样本中分数大于或等于120分的频率,从而求出人数,再根据平均数公式即可求解.
【解答】解:(Ⅰ)由题意,得(0.0010+0.0050+0.0100+a+0.0190+0.0250+a+0.0075+0.0025)×10=1,解得a=0.0150;
(Ⅱ)由频率分布直方图,得样本中,分数大于或等于120分的频率为(0.0150+0.0075+0.0025)×10=0.25,
由样本估计总体,得高三年级这次数学考试成绩的优秀率为25%,
这次考试年级优秀人数为1800×25%=450,
设样本的平均分数为,
=(65×0.0010+75×0.0050+85×0.0100+95×0.0150+105×0.0190+115×0.0250+125×0.0150+135×0.0075+145×0.0025)×10=108.35,
由样本估计总体,估计这次考试平均分数为108.35分,
这次数学考试,估计优秀人数有450人,平均分数为108.35分.
【点评】本题考查频率分布直方图的应用,属于基础题.
19.网络直播带货助力乡村振兴,它作为一种新颖的销售土特产的方式,受到社会各界的追捧.某直播间开展地标优品带货直播活动,其主播直播周期次数x(其中10场为一个周期)与产品销售额y(千元)的数据统计如下:
直播周期数x 1 2 3 4 5
产品销售额y(千元) 3 7 15 30 40
根据数据特点,甲认为样本点分布在指数型曲线y=2bx+a的周围,据此他对数据进行了一些初步处理.如下表:
3.7 55 382 65 978 101
其中zi=log2yi,=
(1)请根据表中数据,建立y关于x的回归方程(系数精确到0.01);
(2)①乙认为样本点分布在直线y=mx+n的周围,并计算得回归方程为=9.7x﹣10.1,以及该回归模型的相关指数R乙2=0.98,试比较甲、乙两人所建立的模型,谁的拟合效果更好?
②由①所得的结论,计算该直播间欲使产品销售额达到8万元以上,直播周期数至少为多少?(最终答案精确到1)
附:对于一组数据 (u1,v1)(u2,v2),…,(un,vn),其回归直线=+u的斜率和截距的最小二乘估计分别为=,=,相关系数:R2=1﹣.
【分析】(1)对y=2bx+a两边取对数,得log2y=bx+a,设z=log2y,有z=bx+a,根据已知数据求出z关于x的回归方程,即可得y关于x的回归方程;
(2)①计算可得R甲2≈0.90<0.98,再由相关系数越大,拟合效果越好,得解;
②令=9.7x﹣10.1>8,求出x的范围,即可.
【解答】解:(1)对y=2bx+a两边取对数,得log2y=(bx+a)log22=bx+a,
设z=log2y,则z=bx+a,
由表中数据可知,=×(1+2+3+4+5)=3,
所以===0.95,=﹣=3.7﹣0.95×3=0.85,
所以=0.95x+0.85,
所以log2y=0.95x+0.85,即y=20.95x+0.85,
故y关于x的回归方程为y=20.95x+0.85.
(2)①R甲2=1﹣=1﹣≈0.90<0.98,
所以乙建立的模型拟合效果更好.
②令=9.7x﹣10.1>8,解得x>≈1.9,
故该直播间欲使产品销售额达到8万元以上,直播周期数至少为2次.
【点评】本题考查回归方程的求法与应用,相关系数的含义,考查逻辑推理能力和运算能力,属于中档题.
20.据统计,某校高三打印室1﹣4月份购买的打印纸的箱数如表:
月份代号t 1 2 3 4
打印纸的数量y(箱) 60 65 70 85
(1)求相关系数r,并从r的角度分析能否用线性回归模型拟合y与t的关系(若|r|≥0.75,则线性相关程度很强,可用线性回归模型拟合);
(2)建立y关于t的回归方程,并用其预测5月份该校高三打印室需购买的打印纸约为多少箱.
参考公式:对于一组具有线性相关关系的数据(xi,yi)(i=1,2,3, ,n),其回归直线的斜率和截距的最小二乘估计分别为=,.
相关系数,参考数据:
【分析】(1)利用相关系数公式结合条件即得;
(2)根据最小二乘法可得线性回归直线方程,然后将t=5代入回归方程即得.
【解答】解:(1)由已知数据可得=,
又852=19950,,
所以===,
因为r>0.75,所以线性相关程度很强,可用线性回归模型拟合y与t的关系;
(2)因为b====8,,
所以y关于t的回归方程为y=8t+50,
将t=5代入回归方程,得箱,
所以预测5月份该校高三打印室需购买的打印纸约为90箱.
【点评】本题主要考查了相关系数的计算,考查了线性回归方程的应用,属于中档题.
21.中国男篮历史上曾12次参加亚运会,其中8次夺得金牌,是亚运会夺冠次数最多的球队.第19届亚运会将于2023年9月23日至10月8日在杭州举办.
(1)为了解喜爱篮球运动是否与性别有关,某学校随机抽取了男生和女生各100名进行调查,得到2×2列联表如下:
喜爱篮球 不喜爱篮球合计
男生 65 35 100
女生 25 75 100
合计 90 110 200
依据小概率值α=0.001的独立性检验,能否认为喜爱篮球运动与性别有关?
(2)校篮球队中的甲、乙、丙三名球员将进行传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,第n次触球者是甲的概率记为Pn,即P1=1.
(i)求P3,P4,并证明:为等比数列;
(ii)比较第15次触球者是甲与第15次触球者是乙的概率的大小.
参考公式:,其中n=a+b+c+d为样本容量.
参考数据:
P(K2≥k) 0.10 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
【分析】(1)假设H0:喜爱足球运动与性别独立,即喜爱足球运动与性别无关,计算K2,对照附表即可得出结论.
(2)(i)根据题意写出P3、P4的值,第n次触球者是甲的概率记为Pn,n≥2时,第n﹣1次触球者是甲的概率为Pn﹣1,第n﹣1次触球者不是甲的概率为1﹣Pn﹣1,由此得出Pn﹣=﹣(Pn﹣1﹣),即可判断{Pn﹣}是等比数列;
(ii)写出Pn,计算P15和Q15=(1﹣P15)的值,比较大小即可.
【解答】解:(1)假设H0:喜爱足球运动与性别独立,即喜爱足球运动与性别无关,
计算K2=≈32.323>10.828,
根据小概率值α=0.001的独立性检验,我们推断H0不成立,
即认为喜爱足球运动与性别有关,此推断犯错误的概率不超过0.001.
(2)(i)由题意知,P1=1,P2=0,P3=,P4=×0+(1﹣)×=;
证明:第n次触球者是甲的概率记为Pn,
则当n≥2时,第n﹣1次触球者是甲的概率为Pn﹣1,
第n﹣1次触球者不是甲的概率为1﹣Pn﹣1,
则Pn=Pn﹣1×0+(1﹣Pn﹣1)×=(1﹣Pn﹣1),
从而Pn﹣=﹣(Pn﹣1﹣),
又P1﹣=,
所以{Pn﹣}是以为首项,公比为﹣的等比数列,
(ii)第n次触球者是甲的概率为Pn=×+,
所以P15=×+=×+>,
第15次触球者是乙的概率为Q15=(1﹣P15)=(1﹣×﹣)=﹣×<,
所以第15次触球者是甲的概率比第15次触球者是乙的概率大.
【点评】本题考查了列联表与独立性检验应用问题,也考查了概率与统计的应用问题,是难题.
22.2022年11月17日,由工业和信息化部、安徽省人民政府共同主办的第十七届“中国芯”集成电路产业大会在合肥成功举办.此次大会以“强芯固基以质为本”为主题,旨在培育壮大我国集成电路产业,夯实产业基础、营造良好产业生态.2022年,全国芯片研发单位相比2006年增加194家,提交芯片数量增加299个,均增长超过6倍.某芯片研发单位用在“A芯片”上研发费用占本单位总研发费用的百分比y(%)如表所示.
年份 2016 2017 2018 2019 2020 2021 2022
年份代码 1 2 3 4 5 6 7
y 20% 30% 32% 39% 42% 46% 50%
(1)根据表中的数据,作出相应的折线图;并结合相关数据,计算相关系数r,并推断y与t线性相关程度;(已知:0.8≤|r|≤1,则认为y与t线性相关很强;0.3≤|r|<0.8,则认为y与t线性相关一般;|r|<0.3,则认为y与t线性相关较弱)
(2)求出y与t的回归直线方程(保留一位小数);
(3)请判断,若2024年用在“A芯片”上研发费用不低于295万元,则该单位2024年芯片研发的总费用预算为500万元是否符合研发要求?
附:相关数据:,,,.
相关计算公式:①相关系数;
在回归直线方程中,,.
【分析】(1)根据表格数据可绘制折线图,结合公式可求得相关系数r,对比已知线性相关强度判断依据即可得到结论;
(2)采用最小二乘法即可求得回归直线;
(3)将t=9代入回归直线可求得,进而计算得到预算为500万元时的研发费用的预估值,由此可得结论.
【解答】解:(1)折线图如下:
由题意得:,∴,∴,
∴,
∵|0.98|>0.8,∴y与t线性相关很强;
(2)由题意得:,∴,
∴y关于t的回归直线方程为;
(3)2024年对应的年份代码t=9,则当t=9时,,
∴预测2024年用在“A芯片”上的研发费用约为500×60.5%=302.5(万元),
∵302.5>295,∴符合研发要求.
【点评】本题主要考查了利用最小二乘法求回归直线方程,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
