人教版数学七年级下册7.1.2平面直角坐标系 同步练习(含答案)
文档属性
| 名称 | 人教版数学七年级下册7.1.2平面直角坐标系 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 641.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 19:21:34 | ||
图片预览


文档简介
7.1.2平面直角坐标系
一、单选题
1.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“炮”的点的坐标分别为,,则表示棋子“車”的点的坐标为( )
A. B. C. D.
2.在如图所示的平面直角坐标系中,点B的坐标为( )
A. B. C. D.
3.点P在x轴上,且到原点的距离为3,则点P的坐标是( )
A. B. C.或 D.或
4.若在轴上,则到轴的距离是( )
A. B.1 C.2 D.3
5.在平面直角坐标系中,已知点,,下列说法:①直线轴;②点A与点B的距离为6个单位长度;③点B到两坐标轴的距离相等;④连接,则为钝角;其中错误的说法的个数是( )
A.0 B.1 C.3 D.4
6.平面直角坐标系内有一点,已知,满足,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是( )
A. B. C. D.
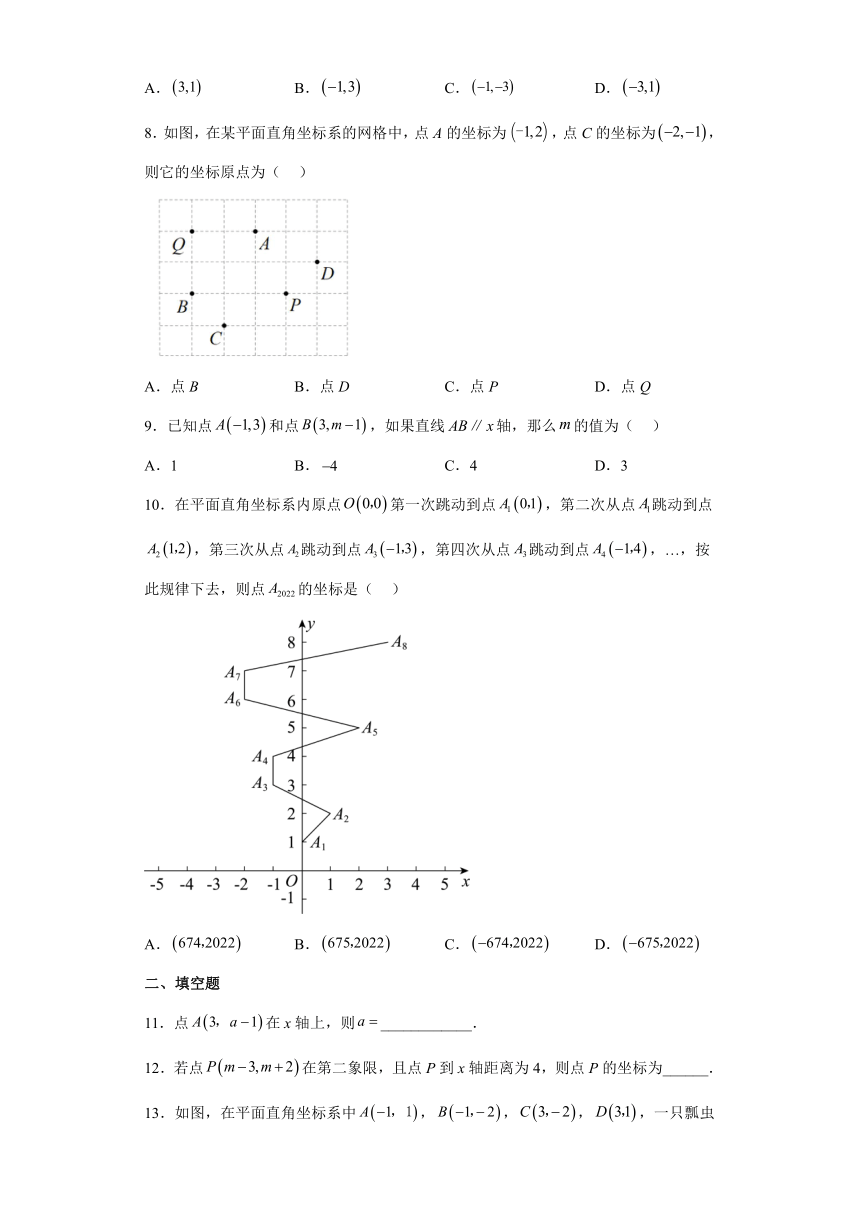
8.如图,在某平面直角坐标系的网格中,点A的坐标为,点C的坐标为,则它的坐标原点为( )
A.点B B.点D C.点P D.点Q
9.已知点和点,如果直线轴,那么的值为( )
A.1 B. C.4 D.3
10.在平面直角坐标系内原点第一次跳动到点,第二次从点跳动到点,第三次从点跳动到点,第四次从点跳动到点,…,按此规律下去,则点的坐标是( )
A. B. C. D.
二、填空题
11.点在x轴上,则____________.
12.若点在第二象限,且点P到x轴距离为4,则点P的坐标为______.
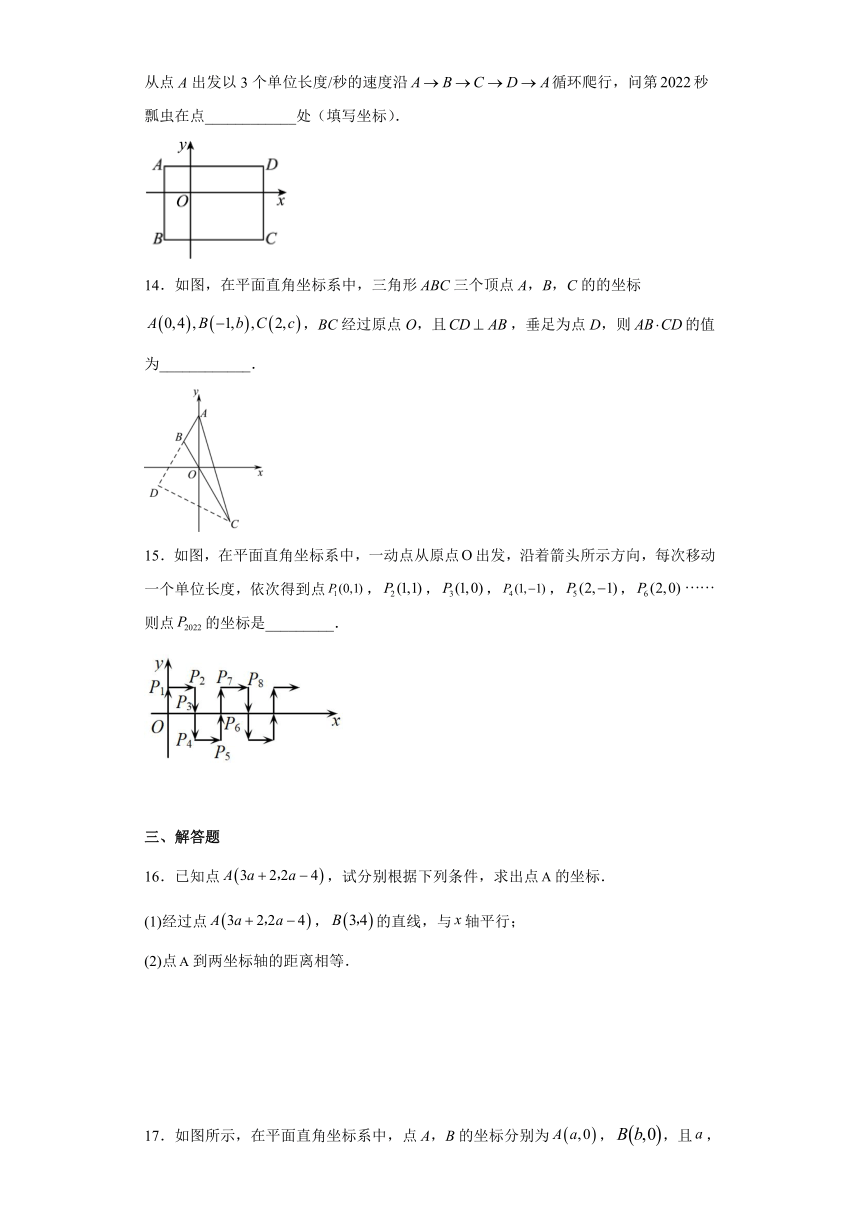
13.如图,在平面直角坐标系中,,,,一只瓢虫从点A出发以3个单位长度/秒的速度沿循环爬行,问第秒瓢虫在点____________处(填写坐标).
14.如图,在平面直角坐标系中,三角形ABC三个顶点A,B,C的的坐标,BC经过原点O,且,垂足为点D,则的值为____________.
15.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头所示方向,每次移动一个单位长度,依次得到点,,,,,则点的坐标是_________.
三、解答题
16.已知点,试分别根据下列条件,求出点的坐标.
(1)经过点,的直线,与轴平行;
(2)点到两坐标轴的距离相等.
17.如图所示,在平面直角坐标系中,点A,B的坐标分别为,,且,满足,点的坐标为.
(1)求,的值及;
(2)若点在轴上,且,试求点的坐标.
18.如图,已知在平面直角坐标系中,OA=OB=4,BC=12,点P的坐标是(a,6).
(1)直接写出ABC顶点A,C的坐标;
(2)若点P坐标为(1,6),连接PA,PB,求PAB的面积;
(3)是否存在点P,使PAB的面积等于ABC的面积?如果存在,请求出点P的坐标.
参考答案
1.C
2.A
3.D
4.C
5.A
6.B
7.B
8.C
9.C
10.C
11.1
12.
13.
14.12
15.
16.(1)解:∵经过点,的直线,与轴平行,
∴点A和点B的纵坐标相同,
∴,
∴,
∴,
∴点的坐标为;
(2)解:∵点到两坐标轴的距离相等,
∴,
∴或,
解得或,
当时,,
当时,,.
故点的坐标为或.
17.(1)∵,
∴,,
∴,,
∴点,点.
又∵点,
∴,,
∴.
(2)设点的坐标为,则,
又∵,
∴,
∴,
∴,
即,
解得:或,
故点的坐标为或.
18. (1)∵OA=OB=4,BC=12,
∴A(0,4),OC=12﹣4=8,
∴C(8,0);
(2)
连接OP,如图1所示:
∵点P坐标为(1,6),
∴△PAB的面积=△POB的面积﹣△AOB的面积﹣△OAP的面积=×4×6﹣×4×4﹣ ×4×1=2;
(3)
存在点P,使△PAB的面积等于△ABC的面积,理由如下:
∵点P的坐标是(a,6),
∴点P在直线y=6上运动,
分两种情况:
①当点P在y轴左侧时,a<0,
连接OP,如图2所示:
∵△PAB的面积=△OPB的面积+△OAP的面积﹣△AOB的面积,△PAB的面积=△ABC的面积,
∴×4×6+×4×(﹣a)﹣×4×4=×12×4,
解得:a=﹣10,
∴P(﹣10,6);
②当点P在y轴右侧时,a>0,
连接OP、CP,如图3所示:
∵△PAB的面积=△AOB的面积+AOP的面积+△OCP的面积﹣△BCP的面积,△PAB的面积=△ABC的面积,
∴×4×4+×4×a+×8×6﹣×12×6=×12×4,
解得:a=14,
∴P(14,6);
综上所述,存在点P,使△PAB的面积等于△ABC的面积,点P的坐标为(﹣10,6)或(14,6).
一、单选题
1.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“炮”的点的坐标分别为,,则表示棋子“車”的点的坐标为( )
A. B. C. D.
2.在如图所示的平面直角坐标系中,点B的坐标为( )
A. B. C. D.
3.点P在x轴上,且到原点的距离为3,则点P的坐标是( )
A. B. C.或 D.或
4.若在轴上,则到轴的距离是( )
A. B.1 C.2 D.3
5.在平面直角坐标系中,已知点,,下列说法:①直线轴;②点A与点B的距离为6个单位长度;③点B到两坐标轴的距离相等;④连接,则为钝角;其中错误的说法的个数是( )
A.0 B.1 C.3 D.4
6.平面直角坐标系内有一点,已知,满足,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是( )
A. B. C. D.
8.如图,在某平面直角坐标系的网格中,点A的坐标为,点C的坐标为,则它的坐标原点为( )
A.点B B.点D C.点P D.点Q
9.已知点和点,如果直线轴,那么的值为( )
A.1 B. C.4 D.3
10.在平面直角坐标系内原点第一次跳动到点,第二次从点跳动到点,第三次从点跳动到点,第四次从点跳动到点,…,按此规律下去,则点的坐标是( )
A. B. C. D.
二、填空题
11.点在x轴上,则____________.
12.若点在第二象限,且点P到x轴距离为4,则点P的坐标为______.
13.如图,在平面直角坐标系中,,,,一只瓢虫从点A出发以3个单位长度/秒的速度沿循环爬行,问第秒瓢虫在点____________处(填写坐标).
14.如图,在平面直角坐标系中,三角形ABC三个顶点A,B,C的的坐标,BC经过原点O,且,垂足为点D,则的值为____________.
15.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头所示方向,每次移动一个单位长度,依次得到点,,,,,则点的坐标是_________.
三、解答题
16.已知点,试分别根据下列条件,求出点的坐标.
(1)经过点,的直线,与轴平行;
(2)点到两坐标轴的距离相等.
17.如图所示,在平面直角坐标系中,点A,B的坐标分别为,,且,满足,点的坐标为.
(1)求,的值及;
(2)若点在轴上,且,试求点的坐标.
18.如图,已知在平面直角坐标系中,OA=OB=4,BC=12,点P的坐标是(a,6).
(1)直接写出ABC顶点A,C的坐标;
(2)若点P坐标为(1,6),连接PA,PB,求PAB的面积;
(3)是否存在点P,使PAB的面积等于ABC的面积?如果存在,请求出点P的坐标.
参考答案
1.C
2.A
3.D
4.C
5.A
6.B
7.B
8.C
9.C
10.C
11.1
12.
13.
14.12
15.
16.(1)解:∵经过点,的直线,与轴平行,
∴点A和点B的纵坐标相同,
∴,
∴,
∴,
∴点的坐标为;
(2)解:∵点到两坐标轴的距离相等,
∴,
∴或,
解得或,
当时,,
当时,,.
故点的坐标为或.
17.(1)∵,
∴,,
∴,,
∴点,点.
又∵点,
∴,,
∴.
(2)设点的坐标为,则,
又∵,
∴,
∴,
∴,
即,
解得:或,
故点的坐标为或.
18. (1)∵OA=OB=4,BC=12,
∴A(0,4),OC=12﹣4=8,
∴C(8,0);
(2)
连接OP,如图1所示:
∵点P坐标为(1,6),
∴△PAB的面积=△POB的面积﹣△AOB的面积﹣△OAP的面积=×4×6﹣×4×4﹣ ×4×1=2;
(3)
存在点P,使△PAB的面积等于△ABC的面积,理由如下:
∵点P的坐标是(a,6),
∴点P在直线y=6上运动,
分两种情况:
①当点P在y轴左侧时,a<0,
连接OP,如图2所示:
∵△PAB的面积=△OPB的面积+△OAP的面积﹣△AOB的面积,△PAB的面积=△ABC的面积,
∴×4×6+×4×(﹣a)﹣×4×4=×12×4,
解得:a=﹣10,
∴P(﹣10,6);
②当点P在y轴右侧时,a>0,
连接OP、CP,如图3所示:
∵△PAB的面积=△AOB的面积+AOP的面积+△OCP的面积﹣△BCP的面积,△PAB的面积=△ABC的面积,
∴×4×4+×4×a+×8×6﹣×12×6=×12×4,
解得:a=14,
∴P(14,6);
综上所述,存在点P,使△PAB的面积等于△ABC的面积,点P的坐标为(﹣10,6)或(14,6).
