2023年中考数学复习 二次函数(含答案)
文档属性
| 名称 | 2023年中考数学复习 二次函数(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 455.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 19:32:24 | ||
图片预览



文档简介
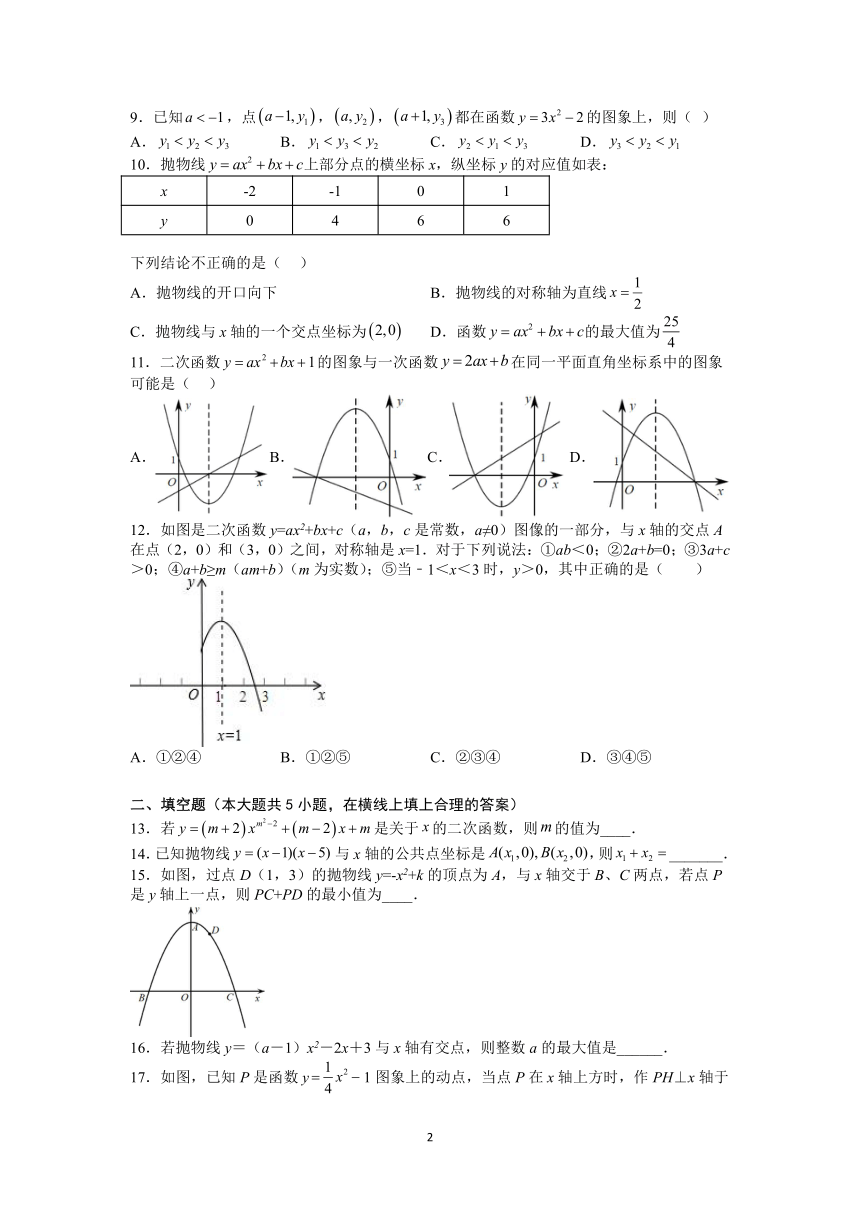
2023年中考数学复习:二次函数
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共12小题,在每小题列出的选项中,选出符合题目的一项)
1.抛物线的顶点坐标是( )
A. B. C. D.
2.关于二次函数的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
3.抛物线的顶点坐标为( )
A. B. C. D.
4.将抛物线向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).
A.; B.;
C.; D..
5.二次函数的部分图像如图所示,可知方程的所有解的积为( )
A.-4 B.4 C.5 D.-5
6.点A(m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上.若y1<y2,则m的取值范围为( )
A. B. C. D.
7.已知二次函数,其中、,则该函数的图象可能为( )
A.B.C.D.
8.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
9.已知,点,,都在函数的图象上,则( )
A. B. C. D.
10.抛物线上部分点的横坐标x,纵坐标y的对应值如表:
x -2 -1 0 1
y 0 4 6 6
下列结论不正确的是( )
A.抛物线的开口向下 B.抛物线的对称轴为直线
C.抛物线与x轴的一个交点坐标为 D.函数的最大值为
11.二次函数的图象与一次函数在同一平面直角坐标系中的图象可能是( )
A.B.C.D.
12.如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图像的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
A.①②④ B.①②⑤ C.②③④ D.③④⑤
二、填空题(本大题共5小题,在横线上填上合理的答案)
13.若是关于的二次函数,则的值为____.
14.已知抛物线与x轴的公共点坐标是,则_______.
15.如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为____.
16.若抛物线y=(a-1)x2-2x+3与x轴有交点,则整数a的最大值是______.
17.如图,已知P是函数y1图象上的动点,当点P在x轴上方时,作PH⊥x轴于点H,连接PO.小华用几何画板软件对PO,PH的数量关系进行了探讨,发现PO﹣PH是个定值,则这个定值为 _____.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
18.在平面直角坐标系中,二次函数的图象经过点.
(1)求二次函数的表达式;
(2)求二次函数图象的对称轴.
19.已知函数y=(m2-2)x2+(m+)x+8.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,求m的取值范围.
20.某种商品每件的进价为10元,若每件按20元的价格销售,则每月能卖出360件;若每件按30元的价格销售,则每月能卖出60件.假定每月的销售件数y是销售价格x(单位:元)的一次函数.
(1)求y关于x的一次函数解析式;
(2)当销售价格定为多少元时,每月获得的利润最大?并求此最大利润.
21.冰墩墩是2022年北京冬季奥运会的吉祥物.冰墩墩以熊猫为原型设计,寓意创造非凡、探索未来.某超市用2400元购进一批冰墩墩玩偶出售.若进价降低20%,则可以多买50个.市场调查发现:当每个冰墩墩玩偶的售价是20元时,每周可以销售200个;每涨价1元,每周少销售10个.
(1)求每个冰墩墩玩偶的进价;
(2)设每个冰墩墩玩偶的售价是x元(x是大于20的正整数),每周总利润是w元.
①求w关于x的函数解析式,并求每周总利润的最大值;
②当每周总利润不低于1870元时,求每个冰墩墩玩偶售价x的范围.
22.如图,二次函数的图象与轴的一个交点为,另一个交点为,且与轴交于点.
(1)求二次函数的解析式;
(2)求的面积;
(3)该二次函数图象上是否存在点,使与的面积相等?若存在,请求出点的坐标;若不存在,请说明理由.
23.如图在平面直角坐标系中,一次函数的图像经过点、交反比例函数的图像于点,点在反比例函数的图像上,横坐标为,轴交直线于点,是轴上任意一点,连接、.
(1)求一次函数和反比例函数的表达式;
(2)求面积的最大值.
答案:
1.B 2.D 3.B 4.B 5.D 6.B 7.C 8.C 9.D 10.C 11.A 12.A
13.2 14.6 15. 16.0 17.2
19解:(1)∵二次函数y=x2-2mx+5m的图象经过点(1,-2),
∴-2=1-2m+5m,
解得;
∴二次函数的表达式为y=x2+2x-5.
(2)二次函数图象的对称轴为直线;
故二次函数的对称轴为:直线;
20.(1)由题意得,,解得m=;
(2)由题意得,m2-2≠0,解得m≠且m≠-.
21.(1)解:设,把,和,代入可得
,
解得,
则;
(2)解:每月获得利润
.
∵,
∴当时,P有最大值,最大值为3630.
答:当价格为21元时,才能使每月获得最大利润,最大利润为3630元.
22.(1)设每个冰墩墩钥匙扣的进价为x元,
由题意得:,
解得,
经检验,是原方程的解且符合题意,
答:每个冰墩墩钥匙扣的进价为12元;
(2)①
∵且x是大于20的正整数
∴当时,w有最大值,最大值为1960元
②售价为24元或25元或26元或27元或28元.
解析如下:②由题意得,,
解得或29
∵抛物线开口向下,x是大于20的正整数
∴当时,每周总利润不低于1870元,
23(1)解:∵二次函数的图象与轴的一个交点为,
∴,
解得,
即,
;
(2)存在,或或,
理由如下,
由,令,
即,
解得,
,
;
(3)设,边上的高为,
与的面积相等,
,
是上的点,
则,
或,
解得或.,
或或.
24.解:(1)设直线AB为
把点、代入解析式得:
解得:
直线为
把代入得:
把代入:
,
(2)设 轴,
则 由<<,
即当时,
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共12小题,在每小题列出的选项中,选出符合题目的一项)
1.抛物线的顶点坐标是( )
A. B. C. D.
2.关于二次函数的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
3.抛物线的顶点坐标为( )
A. B. C. D.
4.将抛物线向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).
A.; B.;
C.; D..
5.二次函数的部分图像如图所示,可知方程的所有解的积为( )
A.-4 B.4 C.5 D.-5
6.点A(m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上.若y1<y2,则m的取值范围为( )
A. B. C. D.
7.已知二次函数,其中、,则该函数的图象可能为( )
A.B.C.D.
8.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
9.已知,点,,都在函数的图象上,则( )
A. B. C. D.
10.抛物线上部分点的横坐标x,纵坐标y的对应值如表:
x -2 -1 0 1
y 0 4 6 6
下列结论不正确的是( )
A.抛物线的开口向下 B.抛物线的对称轴为直线
C.抛物线与x轴的一个交点坐标为 D.函数的最大值为
11.二次函数的图象与一次函数在同一平面直角坐标系中的图象可能是( )
A.B.C.D.
12.如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图像的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
A.①②④ B.①②⑤ C.②③④ D.③④⑤
二、填空题(本大题共5小题,在横线上填上合理的答案)
13.若是关于的二次函数,则的值为____.
14.已知抛物线与x轴的公共点坐标是,则_______.
15.如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为____.
16.若抛物线y=(a-1)x2-2x+3与x轴有交点,则整数a的最大值是______.
17.如图,已知P是函数y1图象上的动点,当点P在x轴上方时,作PH⊥x轴于点H,连接PO.小华用几何画板软件对PO,PH的数量关系进行了探讨,发现PO﹣PH是个定值,则这个定值为 _____.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
18.在平面直角坐标系中,二次函数的图象经过点.
(1)求二次函数的表达式;
(2)求二次函数图象的对称轴.
19.已知函数y=(m2-2)x2+(m+)x+8.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,求m的取值范围.
20.某种商品每件的进价为10元,若每件按20元的价格销售,则每月能卖出360件;若每件按30元的价格销售,则每月能卖出60件.假定每月的销售件数y是销售价格x(单位:元)的一次函数.
(1)求y关于x的一次函数解析式;
(2)当销售价格定为多少元时,每月获得的利润最大?并求此最大利润.
21.冰墩墩是2022年北京冬季奥运会的吉祥物.冰墩墩以熊猫为原型设计,寓意创造非凡、探索未来.某超市用2400元购进一批冰墩墩玩偶出售.若进价降低20%,则可以多买50个.市场调查发现:当每个冰墩墩玩偶的售价是20元时,每周可以销售200个;每涨价1元,每周少销售10个.
(1)求每个冰墩墩玩偶的进价;
(2)设每个冰墩墩玩偶的售价是x元(x是大于20的正整数),每周总利润是w元.
①求w关于x的函数解析式,并求每周总利润的最大值;
②当每周总利润不低于1870元时,求每个冰墩墩玩偶售价x的范围.
22.如图,二次函数的图象与轴的一个交点为,另一个交点为,且与轴交于点.
(1)求二次函数的解析式;
(2)求的面积;
(3)该二次函数图象上是否存在点,使与的面积相等?若存在,请求出点的坐标;若不存在,请说明理由.
23.如图在平面直角坐标系中,一次函数的图像经过点、交反比例函数的图像于点,点在反比例函数的图像上,横坐标为,轴交直线于点,是轴上任意一点,连接、.
(1)求一次函数和反比例函数的表达式;
(2)求面积的最大值.
答案:
1.B 2.D 3.B 4.B 5.D 6.B 7.C 8.C 9.D 10.C 11.A 12.A
13.2 14.6 15. 16.0 17.2
19解:(1)∵二次函数y=x2-2mx+5m的图象经过点(1,-2),
∴-2=1-2m+5m,
解得;
∴二次函数的表达式为y=x2+2x-5.
(2)二次函数图象的对称轴为直线;
故二次函数的对称轴为:直线;
20.(1)由题意得,,解得m=;
(2)由题意得,m2-2≠0,解得m≠且m≠-.
21.(1)解:设,把,和,代入可得
,
解得,
则;
(2)解:每月获得利润
.
∵,
∴当时,P有最大值,最大值为3630.
答:当价格为21元时,才能使每月获得最大利润,最大利润为3630元.
22.(1)设每个冰墩墩钥匙扣的进价为x元,
由题意得:,
解得,
经检验,是原方程的解且符合题意,
答:每个冰墩墩钥匙扣的进价为12元;
(2)①
∵且x是大于20的正整数
∴当时,w有最大值,最大值为1960元
②售价为24元或25元或26元或27元或28元.
解析如下:②由题意得,,
解得或29
∵抛物线开口向下,x是大于20的正整数
∴当时,每周总利润不低于1870元,
23(1)解:∵二次函数的图象与轴的一个交点为,
∴,
解得,
即,
;
(2)存在,或或,
理由如下,
由,令,
即,
解得,
,
;
(3)设,边上的高为,
与的面积相等,
,
是上的点,
则,
或,
解得或.,
或或.
24.解:(1)设直线AB为
把点、代入解析式得:
解得:
直线为
把代入得:
把代入:
,
(2)设 轴,
则 由<<,
即当时,
同课章节目录
