2023年中考数学复习 反比例函数(含答案)
文档属性
| 名称 | 2023年中考数学复习 反比例函数(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 755.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 20:40:49 | ||
图片预览



文档简介
2023年中考数学复习:反比例函数
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.给出的六个关系式:①x(y+1);②;③;④;⑤y=;⑥;其中y是x的反比例函数是( )
A.①②③④⑥ B.③⑤⑥ C.①②④ D.④⑥
2.若点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数的图象上,则( )
A.y1>y2>y3 B.y2>y1>y3 C.y3>y1>y2 D.y1>y3>y2
3.若双曲线y=在每一个象限内,y随x的增大而减小,则k的取值范围是( )
A.k<3 B.k≥3 C.k>3 D.k≠3
4.如图,点是反比例函数(,)的图像上任意一点,过点作轴,垂足为.若的面积等于3,则的值等于( )
A. B.6 C. D.3
5.如图,点A是反比例函数图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足分别为B,C,则矩形ABOC的面积为( )
A.-4 B.2 C.4 D.8
6.如图,正比例函数y=mx与反比例函数y=(m、n是非零常数)的图象交于A、B两点.若点A的坐标为(1,2),则点B的坐标是( )
A.(-2,-4)
B.(-2,-1)
C.(-1,-2)
D.(-4,-2)
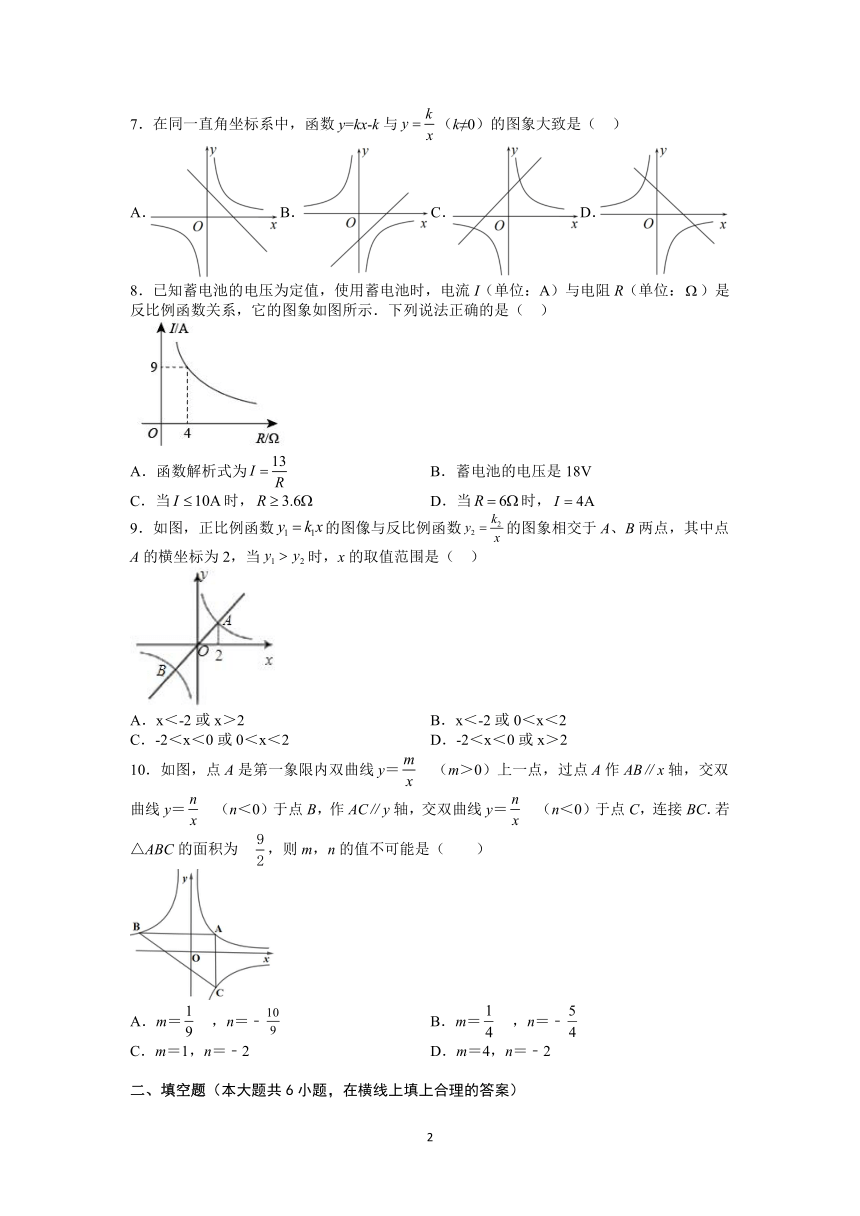
7.在同一直角坐标系中,函数y=kx-k与(k≠0)的图象大致是( )
A.B.C.D.
8.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
9.如图,正比例函数的图像与反比例函数的图象相交于A、B两点,其中点A的横坐标为2,当时,x的取值范围是( )
A.x<-2或x>2 B.x<-2或0<x<2
C.-2<x<0或0<x<2 D.-2<x<0或x>2
10.如图,点A是第一象限内双曲线y= (m>0)上一点,过点A作AB∥x轴,交双曲线y= (n<0)于点B,作AC∥y轴,交双曲线y= (n<0)于点C,连接BC.若△ABC的面积为 ,则m,n的值不可能是( )
A.m= ,n=﹣ B.m= ,n=﹣
C.m=1,n=﹣2 D.m=4,n=﹣2
二、填空题(本大题共6小题,在横线上填上合理的答案)
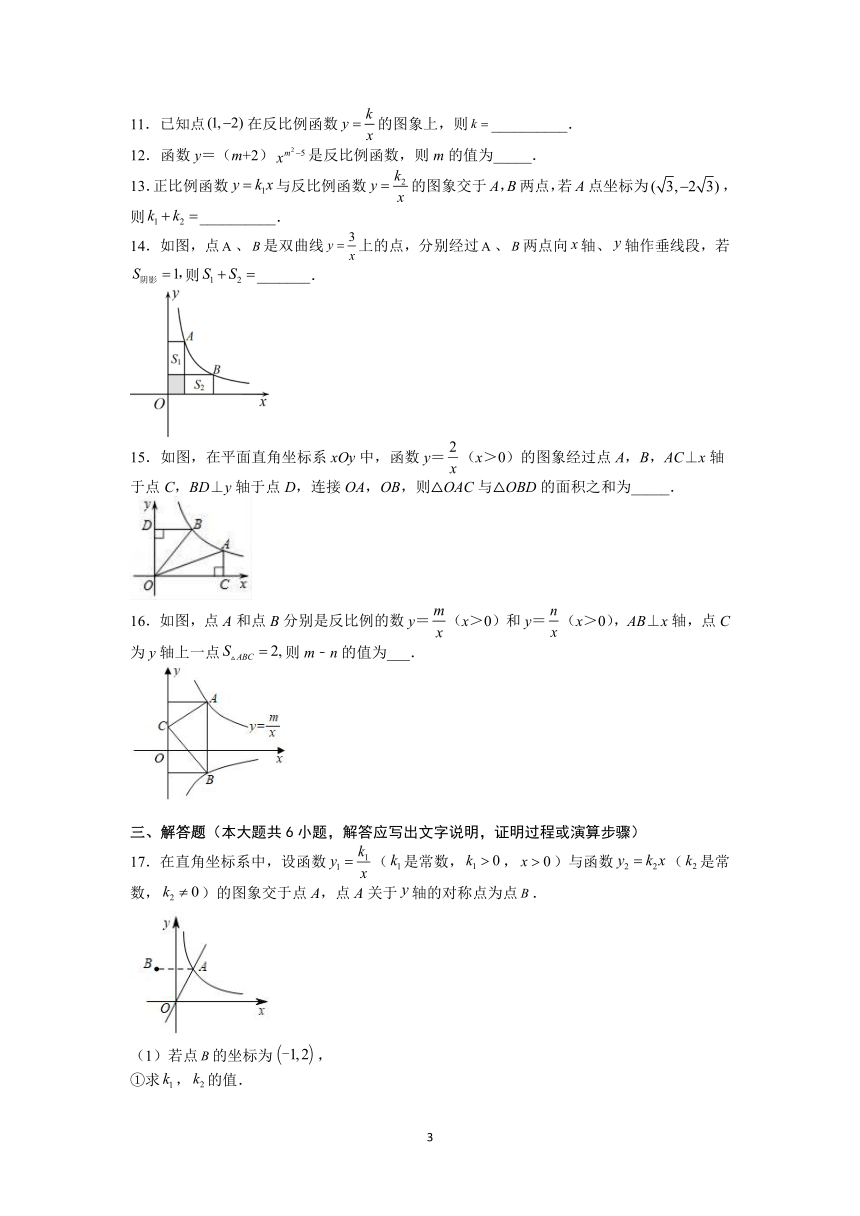
11.已知点在反比例函数的图象上,则__________.
12.函数y=(m+2)是反比例函数,则m的值为_____.
13.正比例函数与反比例函数的图象交于A,B两点,若A点坐标为,则__________.
14.如图,点、是双曲线上的点,分别经过、两点向轴、轴作垂线段,若则_______.
15.如图,在平面直角坐标系xOy中,函数y=(x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,连接OA,OB,则△OAC与△OBD的面积之和为_____.
16.如图,点A和点B分别是反比例的数y=(x>0)和y=(x>0),AB⊥x轴,点C为y轴上一点则m﹣n的值为___.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
17.在直角坐标系中,设函数(是常数,,)与函数(是常数,)的图象交于点A,点A关于轴的对称点为点.
(1)若点的坐标为,
①求,的值.
②当时,直接写出的取值范围.
若点在函数(是常数,)的图象上,求的值.
18.如图,点A在第一象限内,轴于点B,反比例函数的图象分别交于点C,D.已知点C的坐标为.
(1)求k的值及点D的坐标.
(2)已知点P在该反比例函数图象上,且在的内部(包括边界),直接写出点P的横坐标x的取值范围.
19.如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象分别交x轴,y轴于A,B两点,与反比例函数y=(k≠0)的图象交于C,D两点,DE⊥x轴于点E,点C的坐标为(6, 1) ,DE=3.
(1)求反比例函数与一次函数的表达式;
(2)若点P在反比例函数图象上,且△POA的面积等于8,求P点的坐标.
20.如图,已知反比例函数的图像与一次函数的图像交于点,点.
(1)求n和b的值;
(2)求△OAB的面积;
(3)观察图像,不等式的解集为________.
21.截止2021年3月15号,我国自主研发的新冠疫苗已接种超过6200万剂次,疫苗已经经过三期临床试验,测得成人注射一针疫苗后体内抗体浓度y(miu/ml)与注射时间x天之间的函数关系如图所示(当时,y与x是正比例函数关系;当时,y与x是反比例函数关系).
(1)根据图象求当时,y与x之间的函数关系式;
(2)根据图象求当时,y与x之间的函数关系式;
(3)体内抗体浓度不低于140miu/ml的持续时间为多少天?
22.如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知.
(1)求直线的解析式;
(2)求反比例函数的解析式;
(3)点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.
答案:
1.D 2.C 3.C 4.A 5.C 6.C 7.D 8.C 9.D 10.A 11. 12.2
13. 14.4 15.2 16.4
17.解(1)①由题意得,点A的坐标是,
因为函数的图象过点A,
所以,
同理.
②由图象可知,当时,反比例函数的图象位于正比例函数图象的下方,
即当时,.
(2)设点A的坐标是,则点的坐标是,
所以,,
所以.
18.(1)解:把C(2,2)代入,得,,
∴反比例函数函数为(x>0),
∵AB⊥x轴,BD=1,
∴D点纵坐标为1,
把代入,得,
∴点D坐标为(4,1);
(2)解:∵P点在点C(2,2)和点D(4,1)之间,
∴点P的横坐标:;
19.(1)解:∵点C(6,-1)在反比例函数y=(k≠0)的图象上,
∴k=6×(-1)=-6,
∴反比例函数的关系式为y=-,
∵点D在反比例函数y=-上,且DE=3,
∴y=3,代入求得:x=-2,
∴点D的坐标为(-2,3).
∵C、D两点在直线y=ax+b上,则,解得,
∴一次函数的关系式为y=-x+2;
(2)解:设点P的坐标是(m,n).
把y=0代入y=-x+2,解得x=4,
即A(4,0),则OA=4,
∵△POA的面积等于8,
∴×OA×|n|=8,
解得:|n|=4,
∴n1=4,n2=-4,
∴点P的坐标是(-,4)或(,-4).
20.(1)解:由题意,将点代入得:,
解得,
则一次函数的解析式为,
将点代入得:.
(2)解:如图,设一次函数与轴的交点为点,
当时,,解得,即,
,
的面积为.
(3)解:不等式表示的是反比例函数的图像位于一次函数的图像的上方,
则由函数图像得:或,
故答案为:或.
21.解:(1)设当x≤20时,y与x之间的函数关系式是y=kx,
图象过(20,280),
则20k=280,
解得:k=14,
y与x之间的函数关系式是:y=14x,
(2)设当x≥20时,y与x之间的函数关系式是y=,
图象过(20,280), ,
解得:k=5600,
y与x之间的函数关系式是y=;
(3)当x≤20时,140=14x,
解得:x=10.
当x≥20时,140=,
解得:x=40,
故40﹣10+1=31(天),
答:体内抗体浓度不低于140miu/ml的持续时间为31天.
22.解:(1) 点在反比例函数的图象上,
则
设直线为:
则
所以直线为:
(2) 轴, .
所以反比例函数为:
(3)设 而为的中点,
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.给出的六个关系式:①x(y+1);②;③;④;⑤y=;⑥;其中y是x的反比例函数是( )
A.①②③④⑥ B.③⑤⑥ C.①②④ D.④⑥
2.若点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数的图象上,则( )
A.y1>y2>y3 B.y2>y1>y3 C.y3>y1>y2 D.y1>y3>y2
3.若双曲线y=在每一个象限内,y随x的增大而减小,则k的取值范围是( )
A.k<3 B.k≥3 C.k>3 D.k≠3
4.如图,点是反比例函数(,)的图像上任意一点,过点作轴,垂足为.若的面积等于3,则的值等于( )
A. B.6 C. D.3
5.如图,点A是反比例函数图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足分别为B,C,则矩形ABOC的面积为( )
A.-4 B.2 C.4 D.8
6.如图,正比例函数y=mx与反比例函数y=(m、n是非零常数)的图象交于A、B两点.若点A的坐标为(1,2),则点B的坐标是( )
A.(-2,-4)
B.(-2,-1)
C.(-1,-2)
D.(-4,-2)
7.在同一直角坐标系中,函数y=kx-k与(k≠0)的图象大致是( )
A.B.C.D.
8.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
9.如图,正比例函数的图像与反比例函数的图象相交于A、B两点,其中点A的横坐标为2,当时,x的取值范围是( )
A.x<-2或x>2 B.x<-2或0<x<2
C.-2<x<0或0<x<2 D.-2<x<0或x>2
10.如图,点A是第一象限内双曲线y= (m>0)上一点,过点A作AB∥x轴,交双曲线y= (n<0)于点B,作AC∥y轴,交双曲线y= (n<0)于点C,连接BC.若△ABC的面积为 ,则m,n的值不可能是( )
A.m= ,n=﹣ B.m= ,n=﹣
C.m=1,n=﹣2 D.m=4,n=﹣2
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.已知点在反比例函数的图象上,则__________.
12.函数y=(m+2)是反比例函数,则m的值为_____.
13.正比例函数与反比例函数的图象交于A,B两点,若A点坐标为,则__________.
14.如图,点、是双曲线上的点,分别经过、两点向轴、轴作垂线段,若则_______.
15.如图,在平面直角坐标系xOy中,函数y=(x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,连接OA,OB,则△OAC与△OBD的面积之和为_____.
16.如图,点A和点B分别是反比例的数y=(x>0)和y=(x>0),AB⊥x轴,点C为y轴上一点则m﹣n的值为___.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
17.在直角坐标系中,设函数(是常数,,)与函数(是常数,)的图象交于点A,点A关于轴的对称点为点.
(1)若点的坐标为,
①求,的值.
②当时,直接写出的取值范围.
若点在函数(是常数,)的图象上,求的值.
18.如图,点A在第一象限内,轴于点B,反比例函数的图象分别交于点C,D.已知点C的坐标为.
(1)求k的值及点D的坐标.
(2)已知点P在该反比例函数图象上,且在的内部(包括边界),直接写出点P的横坐标x的取值范围.
19.如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象分别交x轴,y轴于A,B两点,与反比例函数y=(k≠0)的图象交于C,D两点,DE⊥x轴于点E,点C的坐标为(6, 1) ,DE=3.
(1)求反比例函数与一次函数的表达式;
(2)若点P在反比例函数图象上,且△POA的面积等于8,求P点的坐标.
20.如图,已知反比例函数的图像与一次函数的图像交于点,点.
(1)求n和b的值;
(2)求△OAB的面积;
(3)观察图像,不等式的解集为________.
21.截止2021年3月15号,我国自主研发的新冠疫苗已接种超过6200万剂次,疫苗已经经过三期临床试验,测得成人注射一针疫苗后体内抗体浓度y(miu/ml)与注射时间x天之间的函数关系如图所示(当时,y与x是正比例函数关系;当时,y与x是反比例函数关系).
(1)根据图象求当时,y与x之间的函数关系式;
(2)根据图象求当时,y与x之间的函数关系式;
(3)体内抗体浓度不低于140miu/ml的持续时间为多少天?
22.如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知.
(1)求直线的解析式;
(2)求反比例函数的解析式;
(3)点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.
答案:
1.D 2.C 3.C 4.A 5.C 6.C 7.D 8.C 9.D 10.A 11. 12.2
13. 14.4 15.2 16.4
17.解(1)①由题意得,点A的坐标是,
因为函数的图象过点A,
所以,
同理.
②由图象可知,当时,反比例函数的图象位于正比例函数图象的下方,
即当时,.
(2)设点A的坐标是,则点的坐标是,
所以,,
所以.
18.(1)解:把C(2,2)代入,得,,
∴反比例函数函数为(x>0),
∵AB⊥x轴,BD=1,
∴D点纵坐标为1,
把代入,得,
∴点D坐标为(4,1);
(2)解:∵P点在点C(2,2)和点D(4,1)之间,
∴点P的横坐标:;
19.(1)解:∵点C(6,-1)在反比例函数y=(k≠0)的图象上,
∴k=6×(-1)=-6,
∴反比例函数的关系式为y=-,
∵点D在反比例函数y=-上,且DE=3,
∴y=3,代入求得:x=-2,
∴点D的坐标为(-2,3).
∵C、D两点在直线y=ax+b上,则,解得,
∴一次函数的关系式为y=-x+2;
(2)解:设点P的坐标是(m,n).
把y=0代入y=-x+2,解得x=4,
即A(4,0),则OA=4,
∵△POA的面积等于8,
∴×OA×|n|=8,
解得:|n|=4,
∴n1=4,n2=-4,
∴点P的坐标是(-,4)或(,-4).
20.(1)解:由题意,将点代入得:,
解得,
则一次函数的解析式为,
将点代入得:.
(2)解:如图,设一次函数与轴的交点为点,
当时,,解得,即,
,
的面积为.
(3)解:不等式表示的是反比例函数的图像位于一次函数的图像的上方,
则由函数图像得:或,
故答案为:或.
21.解:(1)设当x≤20时,y与x之间的函数关系式是y=kx,
图象过(20,280),
则20k=280,
解得:k=14,
y与x之间的函数关系式是:y=14x,
(2)设当x≥20时,y与x之间的函数关系式是y=,
图象过(20,280), ,
解得:k=5600,
y与x之间的函数关系式是y=;
(3)当x≤20时,140=14x,
解得:x=10.
当x≥20时,140=,
解得:x=40,
故40﹣10+1=31(天),
答:体内抗体浓度不低于140miu/ml的持续时间为31天.
22.解:(1) 点在反比例函数的图象上,
则
设直线为:
则
所以直线为:
(2) 轴, .
所以反比例函数为:
(3)设 而为的中点,
同课章节目录
