基本不等式:(广东省珠海市香洲区)
文档属性
| 名称 | 基本不等式:(广东省珠海市香洲区) |  | |
| 格式 | rar | ||
| 文件大小 | 82.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-05 23:04:00 | ||
图片预览




文档简介
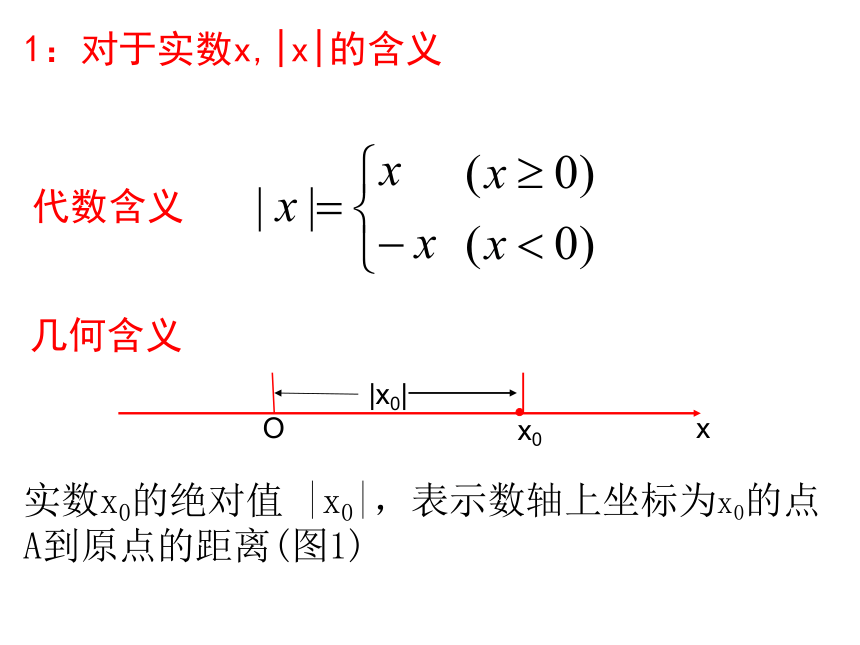
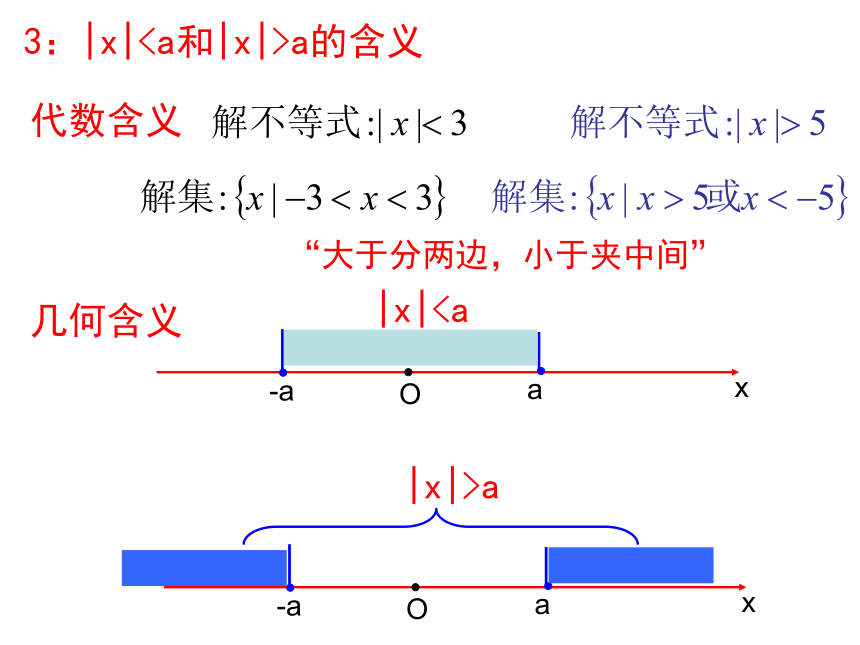
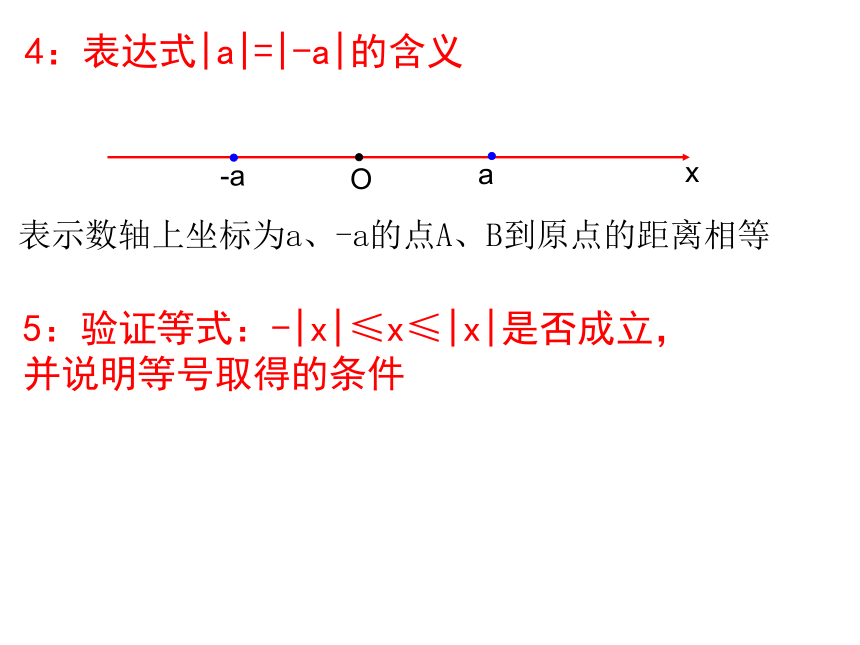
课件15张PPT。绝对值不等式1:对于实数x,|x|的含义代数含义几何含义实数x0的绝对值 |x0|,表示数轴上坐标为x0的点A到原点的距离(图1)|x0|Oxx02:对于实数a,b,|a-b|的含义代数含义几何含义实数a,b的绝对值 |a-b|,表示数轴上坐标为a、b的点A、B到原点的距离(图1)xabO|a-b|试解释:y=|x-3|+|x+1|的几何含义,并求其最值3:|x|a的含义代数含义“大于分两边,小于夹中间”几何含义xaO-a|x|a4:表达式|a|=|-a|的含义xaO-a表示数轴上坐标为a、-a的点A、B到原点的距离相等5:验证等式:-|x|≤x≤|x|是否成立,并说明等号取得的条件6:绝对值不等式的性质不等式有乘、除的不变性,那么不等式相加减有何性质?7、|a| , |b| ,|a+b|之间有何关系?“三角形中,两边之和大于第三边,
两边之差小于第三边““三角形中,两边之和大于第三边,
两边之差小于第三边“(1) 当 不共线时有探究“=”取得的条件(2) 当 共线且同向时有8:在实数范围内,不等式
成立吗? 定理1 如果a,b是实数,则
|a+b| ≤|a| +|b| ,
当且仅当ab≥0时,等号成立。 定理2 如果a,b是实数,则
|a| --|b| ≤ |a+b| ≤|a| +|b| ,| |a,b同号,取“=”a,b异号,取“=”推论1: 推论2: 证明:在定理中以 即: a,b异号,取“=”2006—2007学年度广东省高三年级水平测试.
函数的最小值为--------------------定理2 如果a,b,c是实数,那么
当且仅当(a-b)(b-c)≥0时,等号成立几何含义实数a,b的绝对值 |a-b|,表示数轴上坐标为a、b的点A、B到原点的距离(图1)xabO|a-b|定理2 如果a,b,c是实数,那么
当且仅当(a-b)(b-c)≥0时,等号成立xac|a-c|1、b在a,c之间b|a-b||b-c|取“=”2、b不在a,c之间xac|a-c|b显然成立小结:1、|a-b|的几何含义及其应用
两边之差小于第三边““三角形中,两边之和大于第三边,
两边之差小于第三边“(1) 当 不共线时有探究“=”取得的条件(2) 当 共线且同向时有8:在实数范围内,不等式
成立吗? 定理1 如果a,b是实数,则
|a+b| ≤|a| +|b| ,
当且仅当ab≥0时,等号成立。 定理2 如果a,b是实数,则
|a| --|b| ≤ |a+b| ≤|a| +|b| ,| |a,b同号,取“=”a,b异号,取“=”推论1: 推论2: 证明:在定理中以 即: a,b异号,取“=”2006—2007学年度广东省高三年级水平测试.
函数的最小值为--------------------定理2 如果a,b,c是实数,那么
当且仅当(a-b)(b-c)≥0时,等号成立几何含义实数a,b的绝对值 |a-b|,表示数轴上坐标为a、b的点A、B到原点的距离(图1)xabO|a-b|定理2 如果a,b,c是实数,那么
当且仅当(a-b)(b-c)≥0时,等号成立xac|a-c|1、b在a,c之间b|a-b||b-c|取“=”2、b不在a,c之间xac|a-c|b显然成立小结:1、|a-b|的几何含义及其应用
