解绝对值不等式(广东省珠海市香洲区)
文档属性
| 名称 | 解绝对值不等式(广东省珠海市香洲区) |  | |
| 格式 | rar | ||
| 文件大小 | 39.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-08-29 18:50:00 | ||
图片预览





文档简介
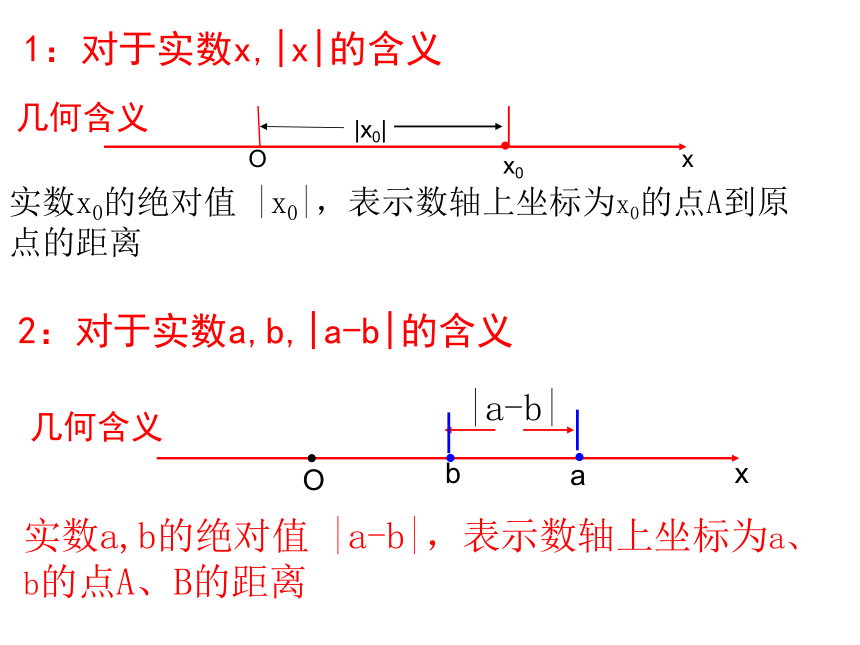
课件16张PPT。绝对值不等式的解法1:对于实数x,|x|的含义几何含义实数x0的绝对值 |x0|,表示数轴上坐标为x0的点A到原点的距离|x0|Oxx02:对于实数a,b,|a-b|的含义几何含义实数a,b的绝对值 |a-b|,表示数轴上坐标为a、b的点A、B的距离xabO|a-b|观察、思考:
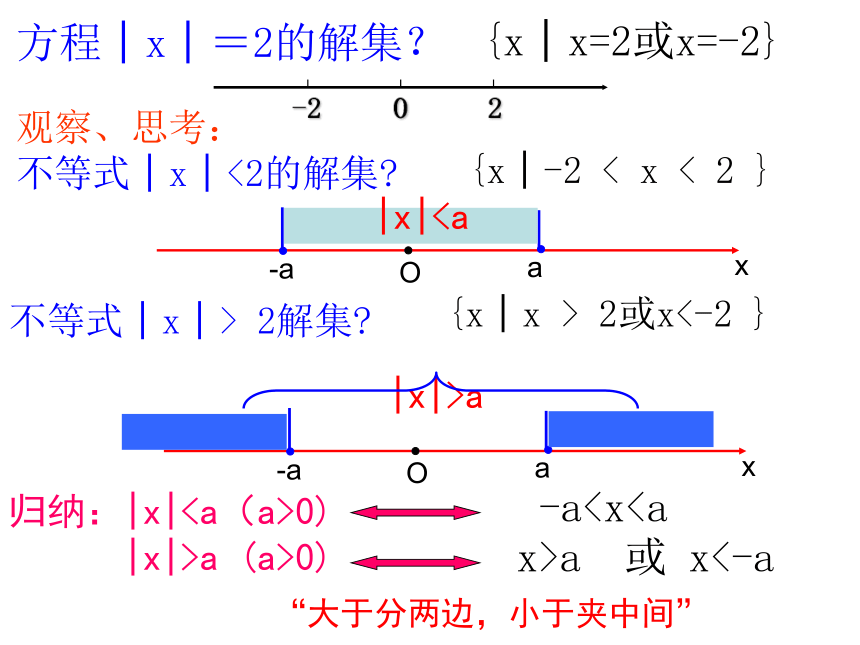
不等式│x│<2的解集?方程│x│=2的解集?{x│x=2或x=-2}{x│-2 < x < 2 }不等式│x│> 2解集?{x│x > 2或x<-2 }-aa 或 x<-axaO-a|x|a归纳:|x|0)
|x|>a (a>0)“大于分两边,小于夹中间”如果把|x|<2中的x换成“x-1”,也就是|x-1|<2如何解?引伸: 解题反思:如果把|x|>2中的x换成“3x-1”,也就是|3x-1|>2如何解?整体换元。例 1 解不等式 解:这个不等式等价于因此,不等式的解集是(–1,4)例 2 解不等式解:这个不等式等价于∴ 原不等式的解集是
(4,+∞)∪ (-∞,-1)。注:最后要写成区间或集合的形式归纳:型如| f(x)|a (a>0)
不等式的解法:“小于夹中间”“大于分两边”巩固练习:
求下列不等式的解集
|2x+1|<5
3<|1-4x|<9
|x2-5x|>-6
3<| 2x+1 | <5(-3,2)(-∞,-1/2)∪(1,+ ∞)R(-3,-2)∪(1,2) 例:解不等式 | 5x-6 | < 6 – x引伸:
型如 | f(x)|a的不等式中
“a”用代数式替换,如何解?解:对绝对值里面的代数式符号讨论:5x-6 ≥ 0 5x-6<6-x(Ⅰ) 或 (Ⅱ) 5x-6<0-(5x-6)<6-x解(Ⅰ)得:6/5≤x<2解(Ⅱ) 得:00 所以00时,转化为-(6-x)<5x-6<(6-x)由绝对值的意义,原不等式转化为:6-x>0-(6-x)<5x-6<(6-x)综合得0|f(x)||f(x)|>g(x) f(x)>g(x) 或f(x)<--g(x) 解不等式 | 5x-6 | < 6 – x进一步反思:不等式组中6-x>0是否可以去掉6-x>0-(6-x)<5x-6<(6-x)6-x≤0无解练习:把下列绝对值不等式转化为同解的非绝对值不等式。3、| x-1 | > 2( x-3)1、|2x-3|<5x 2、|x2-3x-4|>4-x类型2例如:方法1:几何意义方法2:去绝对值方法3:函数的观点距离的观点零点分段法零点分段法、分段函数 注:每段求出的解集需要和小前提求交集,最后各段求并集解不等式 课堂小结:(1)数学知识:
常见的绝对值不等式的解法(2)数学思想分类讨论的思想整体的思想数形结合的思想
不等式│x│<2的解集?方程│x│=2的解集?{x│x=2或x=-2}{x│-2 < x < 2 }不等式│x│> 2解集?{x│x > 2或x<-2 }-a
|x|>a (a>0)“大于分两边,小于夹中间”如果把|x|<2中的x换成“x-1”,也就是|x-1|<2如何解?引伸: 解题反思:如果把|x|>2中的x换成“3x-1”,也就是|3x-1|>2如何解?整体换元。例 1 解不等式 解:这个不等式等价于因此,不等式的解集是(–1,4)例 2 解不等式解:这个不等式等价于∴ 原不等式的解集是
(4,+∞)∪ (-∞,-1)。注:最后要写成区间或集合的形式归纳:型如| f(x)|
不等式的解法:“小于夹中间”“大于分两边”巩固练习:
求下列不等式的解集
|2x+1|<5
3<|1-4x|<9
|x2-5x|>-6
3<| 2x+1 | <5(-3,2)(-∞,-1/2)∪(1,+ ∞)R(-3,-2)∪(1,2) 例:解不等式 | 5x-6 | < 6 – x引伸:
型如 | f(x)|
“a”用代数式替换,如何解?解:对绝对值里面的代数式符号讨论:5x-6 ≥ 0 5x-6<6-x(Ⅰ) 或 (Ⅱ) 5x-6<0-(5x-6)<6-x解(Ⅰ)得:6/5≤x<2解(Ⅱ) 得:0
常见的绝对值不等式的解法(2)数学思想分类讨论的思想整体的思想数形结合的思想
