吉林省长春市第56中学2022-2023学年第二学期九年级数学3月阶段检测试题(PDF版,无答案)
文档属性
| 名称 | 吉林省长春市第56中学2022-2023学年第二学期九年级数学3月阶段检测试题(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 603.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 10:30:53 | ||
图片预览



文档简介
56 中学九年级阶段检测数学试卷
考试时间:120 分钟 满分:120 分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第 I卷(选择题)
一、单选题(每小题 3分,共 24分)
1. 2023 ( )
1 1
A.2023 B. 2023 C. D.
2023 2023
2.第 19届亚运会将于 2023年 9月 23日至 10月 8日在中国浙江省杭州市举行,杭州奥体博览城,将成
为杭州 2023年亚运会的主场馆,杭州奥体博览城核心区占地 154.37公顷,建筑总面积 2720000平方米,
将数 2720000用科学记数法表示为( )
A.0.272 107 B. 2.72 106 C. 27.2 105 D. 272 104
3.以下由 6个正方形纸片拼接成的图形中,不能折叠围成正方体的是( ).
A. B.
C. D.
4.下列式子中,属于最简二次根式的是( )
A. 18 B. 20 C 1. D. 7
3
3x 2 1
5.已知不等式组 ,其解集在数轴上表示正确的是( )
2x 4
A. B.
C. D.
6.如图,在 ABC中, AC 2, B 45 , C 30 ,则 BC的长度为( )
A. 3 B.2 C.1 3 D.3
试卷第 1页,共 8页
7.如图,在 ABC中, ACB 2 B,下列尺规作图,不能得到 ADC 2 B的是( )
A. B. C. D.
1
8.如图,在平面直角坐标系中,正比例函数 y kx与反比例函数 y x的图象交于 A,B两点,过 A作 y
k
轴的垂线,交反比例函数 y x 0 的图象于点 C,连接 BC,若 S△ABC 3,则 k的值为( )x
A.2 B.3 C.4 D.5
第 II 卷(非选择题)(本大题共 10 小题,共 78 分)
二、填空题(每小题 3分,共 18分)
9.分解因式: a3 9a ______.
10.关于 x的一元二次方程 kx2 3x 2 0有两个不相等的实数根, k的取值范围是______.
11.如图,AB∥CD∥EF,直线 l1,l2与这三条平行线分别交于点A,C,E和点 B,D,F .已知 AC 3,
AE 7,DF 5,则 BF的长为________.
12.在活动课上,“凌志组”用含30 角的直角三角尺设计风车.如图, C 90 , ABC 30 , AC 2,
将直角三角尺绕点 A逆时针旋转得到△AB C ,使点C 落在 AB边上,此时 B与 B 两点间的距离为 _____.
试卷第 2页,共 8页
13.如图, AB是 O的直径, AC是 O的切线,OC与 O相交于点 D.若 C 40 ,OA 9,则劣弧
BD的长为______.(结果保留 )
14.如图,正方形OABC的顶点 B在抛物线 y 2x2的第一象限的图象上,若点 B的纵坐标是横坐标的 2
倍,则对角线 AC的长为______.
三、解答题(本大题共 10 小题,共 78 分)
2 a 1
15 2a 1 2a 1 2a 1 .(6 分)化简求值: ,其中 2.
16.(6 分)
明明和文文周末相约到某植物园晨练,这个植物园有 A,B,C,D四个入口,他们可随机选择一个人口进
入植物园,假设选择每个入口的可能性相同.
(1)他们其中一人进入植物园时,从 B入口处进入的概率为______.
(2)用树状图或列表法求她们两人选择相同入口进入植物园的概率.
试卷第 3页,共 8页
17.(6 分)
“双减”政策受到各地教育部门的积极响应,某校为增加学生的课外活动时间,现决定增购两种体育器材:
跳绳和毽子.已知跳绳的单价比毽子的单价多 3元,用 800元购买的跳绳数量和用 500元购买的键子数量
相同.求跳绳和毽子的单价分别是多少元?
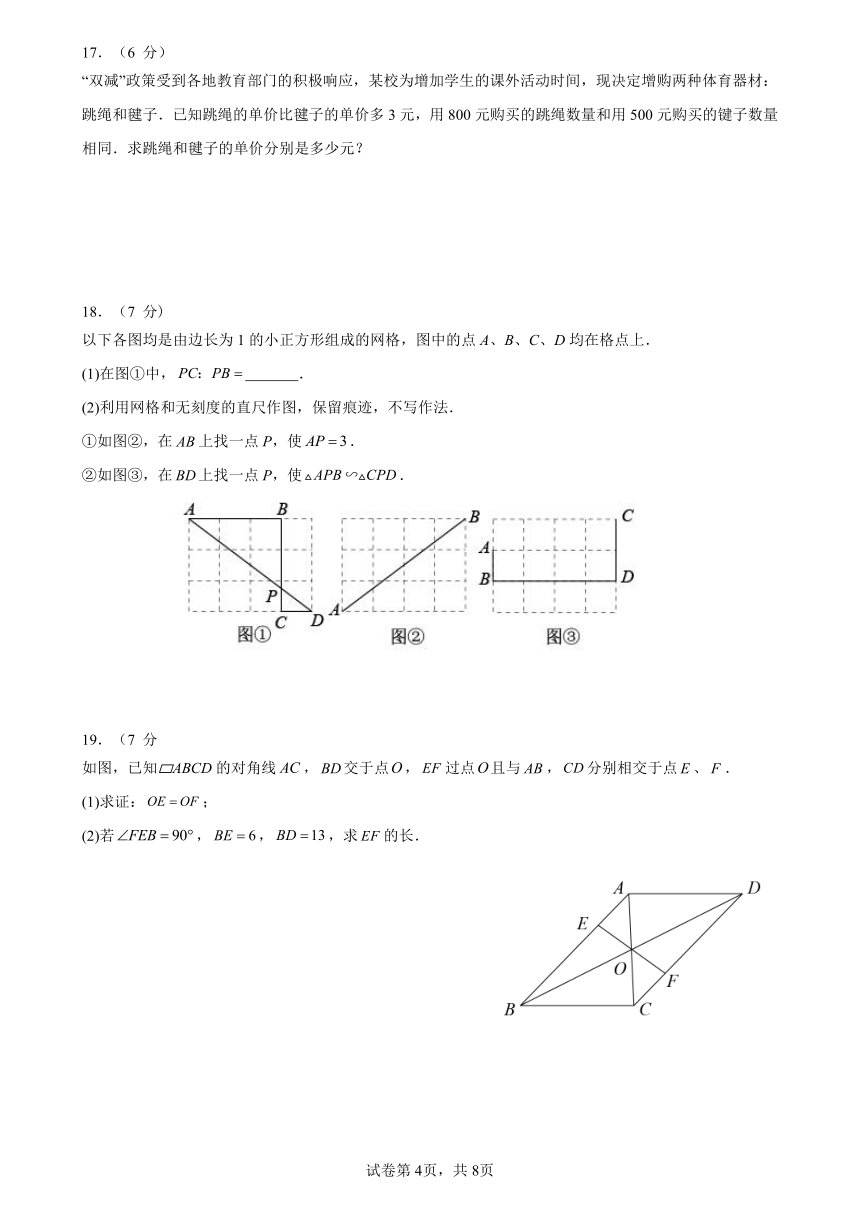
18.(7 分)
以下各图均是由边长为 1的小正方形组成的网格,图中的点 A、B、C、D均在格点上.
(1)在图①中, PC:PB .
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法.
①如图②,在 AB上找一点 P,使 AP 3.
②如图③,在 BD上找一点 P,使 APB∽ CPD.
19.(7 分
如图,已知 ABCD的对角线 AC,BD交于点O, EF 过点O且与 AB,CD分别相交于点 E、 F .
(1)求证:OE OF;
(2)若 FEB 90 , BE 6, BD 13,求 EF 的长.
试卷第 4页,共 8页
20.(7 分)2023年 2月 6日土耳其发生 7.8级地震,牵动世界各国人民的心!为进一步宣传防震减灾科
普知识,增强学生应急避险和自救互救能力,某校组织全校学生进行“防震减灾知识测试”,现随机抽取部
分学生的测试成绩 x(单位:分)整理成 A : 60 x 70,B : 70 x 80,C :80 x 90,D : 90 x 100四
个等级,绘制成如下频数分布表和扇形统计图
被抽取学生的测试成绩的频数表
等级 成绩/分 频数/人 各组总分/分
A 60 x 70 10 650
B 70 x 80 b 1050
C 80 x 90 21 1785
D 90 x 100 5 455
根据以上信息,解答下列问题:
(1)填空:a __________,b _____________;
(2)此次被抽取学生的测试成绩的中位数落在____________等级,求此次被抽取学生的测试成绩的平均数;
(3)如果 90分以上(含 90分)为优秀,请估计全校 2000名学生中此次测试成绩优秀的学生人数.
21.(8 分)
某水果生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温
系统从开启到关闭后,大棚内的温度 y ℃ 与时间 x h 之间的函数关系,其中线段,表示恒温系统开启后阶
段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)这个恒温系统设定的恒定温度为多少℃;
(2)求全天的温度 y与时间 x之间的函数关系式;
(3)若大棚内的温度低于10 ℃ 不利于新品种水果的生长,问这天内,相对有利于水果生长的时间共多少小
时?
试卷第 5页,共 8页
22.(9 分)
感知:数学课上,老师给出了一个模型:如图 1,点 A在直线DE上,且 BDA BAC AEC 90 ,
像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角“模型.
应用:
(1)如图2,Rt△ABC中, ACB 90 ,CB CA,直线 ED经过点C,过A作 AD ED于点D,过B作 BE ED
于点 E.求证: BEC≌ CDA.
(2)如图 3,在 ABC中,D是BC上一点, CAD 90 ,AC AD,
DBA DAB,AB 2 3,求点 C到 AB边的距离.
(3)如图 4,在 ABCD中,E为边 BC上的一点,F为边 AB上的一点.若
EF
DEF B,AB 10,BE 6,求 的值.
DE
试卷第 6页,共 8页
tanB 4
23.(10 分)如图 1,∠C 90
,BC 6, 3,点M 从点 B出发以每秒 1个单位长度的速度向点C
运动,点 N同时从点C出发以每秒 2个单位长度的速度向点 A运动,当一点到达终点时,另一点也停止运
动.
(1)求 AB的长.
(2)当以点K、C、N为顶点的三角形与 ABC相似时,求 t的值.
(3)如图 2,将本题改为点M 从点B出发以每秒 3个单位长度的速度在 BA上向点A运动,点N同时从点A
出发向点C运动,其速度是每秒 2个单位长度,其它条件不变,求当 t为何值时,△MNA为等腰三角形.
试卷第 7页,共 8页
2
24 B 5,0 .(12 分)如图,已知抛物线 y x 4x k与 x轴的一个交点为 ,与 y轴交于点 A,
(1)求抛物线的解析式;
(2)若点 P是抛物线上位于直线 AB上方的动点,分别过点 P作 x轴的平行线交抛物线于点 Q,作 y轴的平
行线交直线 AB于点 D,以 PQ、PD为边作矩形 PQED,求矩形 PQED周长的最大值,并求出此时点 P的
坐标;
(3)若点 N是抛物线对称轴上的一点,在抛物线上是否存在一点 M,使得以 A、N、B、M为顶点的四边形
是平行四边形,若存在,请直接写出点
试卷第 8页,共 8页
试卷第 9页,共 1页
考试时间:120 分钟 满分:120 分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第 I卷(选择题)
一、单选题(每小题 3分,共 24分)
1. 2023 ( )
1 1
A.2023 B. 2023 C. D.
2023 2023
2.第 19届亚运会将于 2023年 9月 23日至 10月 8日在中国浙江省杭州市举行,杭州奥体博览城,将成
为杭州 2023年亚运会的主场馆,杭州奥体博览城核心区占地 154.37公顷,建筑总面积 2720000平方米,
将数 2720000用科学记数法表示为( )
A.0.272 107 B. 2.72 106 C. 27.2 105 D. 272 104
3.以下由 6个正方形纸片拼接成的图形中,不能折叠围成正方体的是( ).
A. B.
C. D.
4.下列式子中,属于最简二次根式的是( )
A. 18 B. 20 C 1. D. 7
3
3x 2 1
5.已知不等式组 ,其解集在数轴上表示正确的是( )
2x 4
A. B.
C. D.
6.如图,在 ABC中, AC 2, B 45 , C 30 ,则 BC的长度为( )
A. 3 B.2 C.1 3 D.3
试卷第 1页,共 8页
7.如图,在 ABC中, ACB 2 B,下列尺规作图,不能得到 ADC 2 B的是( )
A. B. C. D.
1
8.如图,在平面直角坐标系中,正比例函数 y kx与反比例函数 y x的图象交于 A,B两点,过 A作 y
k
轴的垂线,交反比例函数 y x 0 的图象于点 C,连接 BC,若 S△ABC 3,则 k的值为( )x
A.2 B.3 C.4 D.5
第 II 卷(非选择题)(本大题共 10 小题,共 78 分)
二、填空题(每小题 3分,共 18分)
9.分解因式: a3 9a ______.
10.关于 x的一元二次方程 kx2 3x 2 0有两个不相等的实数根, k的取值范围是______.
11.如图,AB∥CD∥EF,直线 l1,l2与这三条平行线分别交于点A,C,E和点 B,D,F .已知 AC 3,
AE 7,DF 5,则 BF的长为________.
12.在活动课上,“凌志组”用含30 角的直角三角尺设计风车.如图, C 90 , ABC 30 , AC 2,
将直角三角尺绕点 A逆时针旋转得到△AB C ,使点C 落在 AB边上,此时 B与 B 两点间的距离为 _____.
试卷第 2页,共 8页
13.如图, AB是 O的直径, AC是 O的切线,OC与 O相交于点 D.若 C 40 ,OA 9,则劣弧
BD的长为______.(结果保留 )
14.如图,正方形OABC的顶点 B在抛物线 y 2x2的第一象限的图象上,若点 B的纵坐标是横坐标的 2
倍,则对角线 AC的长为______.
三、解答题(本大题共 10 小题,共 78 分)
2 a 1
15 2a 1 2a 1 2a 1 .(6 分)化简求值: ,其中 2.
16.(6 分)
明明和文文周末相约到某植物园晨练,这个植物园有 A,B,C,D四个入口,他们可随机选择一个人口进
入植物园,假设选择每个入口的可能性相同.
(1)他们其中一人进入植物园时,从 B入口处进入的概率为______.
(2)用树状图或列表法求她们两人选择相同入口进入植物园的概率.
试卷第 3页,共 8页
17.(6 分)
“双减”政策受到各地教育部门的积极响应,某校为增加学生的课外活动时间,现决定增购两种体育器材:
跳绳和毽子.已知跳绳的单价比毽子的单价多 3元,用 800元购买的跳绳数量和用 500元购买的键子数量
相同.求跳绳和毽子的单价分别是多少元?
18.(7 分)
以下各图均是由边长为 1的小正方形组成的网格,图中的点 A、B、C、D均在格点上.
(1)在图①中, PC:PB .
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法.
①如图②,在 AB上找一点 P,使 AP 3.
②如图③,在 BD上找一点 P,使 APB∽ CPD.
19.(7 分
如图,已知 ABCD的对角线 AC,BD交于点O, EF 过点O且与 AB,CD分别相交于点 E、 F .
(1)求证:OE OF;
(2)若 FEB 90 , BE 6, BD 13,求 EF 的长.
试卷第 4页,共 8页
20.(7 分)2023年 2月 6日土耳其发生 7.8级地震,牵动世界各国人民的心!为进一步宣传防震减灾科
普知识,增强学生应急避险和自救互救能力,某校组织全校学生进行“防震减灾知识测试”,现随机抽取部
分学生的测试成绩 x(单位:分)整理成 A : 60 x 70,B : 70 x 80,C :80 x 90,D : 90 x 100四
个等级,绘制成如下频数分布表和扇形统计图
被抽取学生的测试成绩的频数表
等级 成绩/分 频数/人 各组总分/分
A 60 x 70 10 650
B 70 x 80 b 1050
C 80 x 90 21 1785
D 90 x 100 5 455
根据以上信息,解答下列问题:
(1)填空:a __________,b _____________;
(2)此次被抽取学生的测试成绩的中位数落在____________等级,求此次被抽取学生的测试成绩的平均数;
(3)如果 90分以上(含 90分)为优秀,请估计全校 2000名学生中此次测试成绩优秀的学生人数.
21.(8 分)
某水果生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温
系统从开启到关闭后,大棚内的温度 y ℃ 与时间 x h 之间的函数关系,其中线段,表示恒温系统开启后阶
段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)这个恒温系统设定的恒定温度为多少℃;
(2)求全天的温度 y与时间 x之间的函数关系式;
(3)若大棚内的温度低于10 ℃ 不利于新品种水果的生长,问这天内,相对有利于水果生长的时间共多少小
时?
试卷第 5页,共 8页
22.(9 分)
感知:数学课上,老师给出了一个模型:如图 1,点 A在直线DE上,且 BDA BAC AEC 90 ,
像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角“模型.
应用:
(1)如图2,Rt△ABC中, ACB 90 ,CB CA,直线 ED经过点C,过A作 AD ED于点D,过B作 BE ED
于点 E.求证: BEC≌ CDA.
(2)如图 3,在 ABC中,D是BC上一点, CAD 90 ,AC AD,
DBA DAB,AB 2 3,求点 C到 AB边的距离.
(3)如图 4,在 ABCD中,E为边 BC上的一点,F为边 AB上的一点.若
EF
DEF B,AB 10,BE 6,求 的值.
DE
试卷第 6页,共 8页
tanB 4
23.(10 分)如图 1,∠C 90
,BC 6, 3,点M 从点 B出发以每秒 1个单位长度的速度向点C
运动,点 N同时从点C出发以每秒 2个单位长度的速度向点 A运动,当一点到达终点时,另一点也停止运
动.
(1)求 AB的长.
(2)当以点K、C、N为顶点的三角形与 ABC相似时,求 t的值.
(3)如图 2,将本题改为点M 从点B出发以每秒 3个单位长度的速度在 BA上向点A运动,点N同时从点A
出发向点C运动,其速度是每秒 2个单位长度,其它条件不变,求当 t为何值时,△MNA为等腰三角形.
试卷第 7页,共 8页
2
24 B 5,0 .(12 分)如图,已知抛物线 y x 4x k与 x轴的一个交点为 ,与 y轴交于点 A,
(1)求抛物线的解析式;
(2)若点 P是抛物线上位于直线 AB上方的动点,分别过点 P作 x轴的平行线交抛物线于点 Q,作 y轴的平
行线交直线 AB于点 D,以 PQ、PD为边作矩形 PQED,求矩形 PQED周长的最大值,并求出此时点 P的
坐标;
(3)若点 N是抛物线对称轴上的一点,在抛物线上是否存在一点 M,使得以 A、N、B、M为顶点的四边形
是平行四边形,若存在,请直接写出点
试卷第 8页,共 8页
试卷第 9页,共 1页
同课章节目录
