吉林省长春市赫行实验学校2022-2023学年第二学期九年级数学第一次月考试题(图片版,无答案)
文档属性
| 名称 | 吉林省长春市赫行实验学校2022-2023学年第二学期九年级数学第一次月考试题(图片版,无答案) | 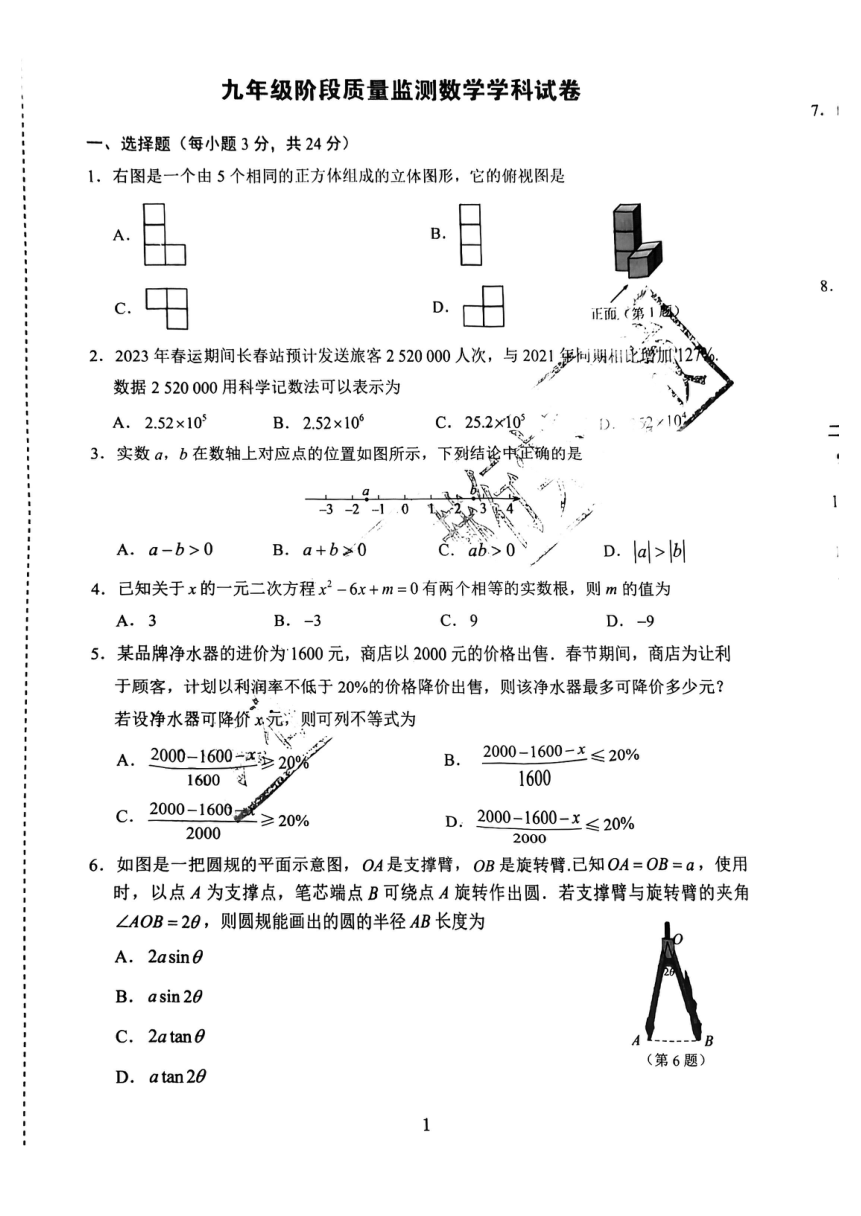 | |
| 格式 | |||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 10:33:05 | ||
图片预览



文档简介
九年级阶段质量监测数学学科试卷
7.1
一、选择题(每小题3分,共24分)
1.右图是一个由5个相同的正方体组成的立体图形,它的俯视图是
8.
D.
正面(第1
2.2023年春运期间长春站预计发送旅客2520000人次,与2021年向明相加12九%
数据2520000用科学记数法可以表示为
A.2.52×10
B.2.52×10
C.25.2×103
210
3,实数a,b在数轴上对应点的位置如图所示,下列结论中确的是
内202g34
A.a-b>0
B.a+b≥0
C.ab.>0
D.a
4.已知关于x的一元二次方程x2-6x+m=0有两个相等的实数根,则m的值为
A.3
B.-3
C.9
D.-9
5.某品牌净水器的进价为1600元,商店以2000元的价格出售.春节期间,商店为让利
于顾客,计划以利润率不低于20%的价格降价出售,则该净水器最多可降价多少元?
若设净水器可降价:元,则可列不等式为
A.
2000-1600-x20%
B.
2000-1600-x≤20%
1600
1600
C
2000-1600≥20%
D.2000-1600-x≤20%
2000
2000
6.如图是一把圆规的平面示意图,OA是支撑臂,OB是旋转臂.已知OA=OB=a,使用
时,以点A为支撑点,笔芯端点B可绕点A旋转作出圆,若支撑臂与旋转臂的夹角
∠AOB=20,则圆规能画出的圆的半径AB长度为
A.2asina
B.asin 26
C.2atan
B
(第6题)
D.atan 20
1
7.已知点P是∠AOB的边OA上一点,根据尺规作图痕迹,射线PQ不一定与OB平行的是
2
D
8.如图,正方形BCD的顶点分别在函数y=依>0)和y=(体0)的图象才D∥y
轴,点C的纵坐标为4,则k+k的值为
A.26
B.28
C.30
D.32
二、填空题(每小题3分,共18分)
0
9.因式分解:a2-2ab=—
(第8题)
10.若代数式】有意义,则实数x的取值范围是
3-x
11.已知v万12.《算法统宗》是我国古代的重要的数学著作,几名学生要凑钱购买1本,若每人出9
元,则多了5元:若每人出8元,则少了2元.问学生人数和该书单价各是多少?若
设学生有x公一书的单价为y元,则可列方程组为一·
13.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个
大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则
大正方形的边长为
D
3
B
123x
(第13题)
(第14题)
14.如图,己知平面直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).二次函
数y=ax2+x+c的图象经过其中任意三个点,当a的值最大时,二次函数的解析式
为
7.1
一、选择题(每小题3分,共24分)
1.右图是一个由5个相同的正方体组成的立体图形,它的俯视图是
8.
D.
正面(第1
2.2023年春运期间长春站预计发送旅客2520000人次,与2021年向明相加12九%
数据2520000用科学记数法可以表示为
A.2.52×10
B.2.52×10
C.25.2×103
210
3,实数a,b在数轴上对应点的位置如图所示,下列结论中确的是
内202g34
A.a-b>0
B.a+b≥0
C.ab.>0
D.a
4.已知关于x的一元二次方程x2-6x+m=0有两个相等的实数根,则m的值为
A.3
B.-3
C.9
D.-9
5.某品牌净水器的进价为1600元,商店以2000元的价格出售.春节期间,商店为让利
于顾客,计划以利润率不低于20%的价格降价出售,则该净水器最多可降价多少元?
若设净水器可降价:元,则可列不等式为
A.
2000-1600-x20%
B.
2000-1600-x≤20%
1600
1600
C
2000-1600≥20%
D.2000-1600-x≤20%
2000
2000
6.如图是一把圆规的平面示意图,OA是支撑臂,OB是旋转臂.已知OA=OB=a,使用
时,以点A为支撑点,笔芯端点B可绕点A旋转作出圆,若支撑臂与旋转臂的夹角
∠AOB=20,则圆规能画出的圆的半径AB长度为
A.2asina
B.asin 26
C.2atan
B
(第6题)
D.atan 20
1
7.已知点P是∠AOB的边OA上一点,根据尺规作图痕迹,射线PQ不一定与OB平行的是
2
D
8.如图,正方形BCD的顶点分别在函数y=依>0)和y=(体0)的图象才D∥y
轴,点C的纵坐标为4,则k+k的值为
A.26
B.28
C.30
D.32
二、填空题(每小题3分,共18分)
0
9.因式分解:a2-2ab=—
(第8题)
10.若代数式】有意义,则实数x的取值范围是
3-x
11.已知v万
元,则多了5元:若每人出8元,则少了2元.问学生人数和该书单价各是多少?若
设学生有x公一书的单价为y元,则可列方程组为一·
13.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个
大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则
大正方形的边长为
D
3
B
123x
(第13题)
(第14题)
14.如图,己知平面直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).二次函
数y=ax2+x+c的图象经过其中任意三个点,当a的值最大时,二次函数的解析式
为
同课章节目录
