2023年中考数学复习 锐角三角函数(含答案)
文档属性
| 名称 | 2023年中考数学复习 锐角三角函数(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 738.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 21:37:51 | ||
图片预览



文档简介
2023年中考数学复习:锐角三角函数
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
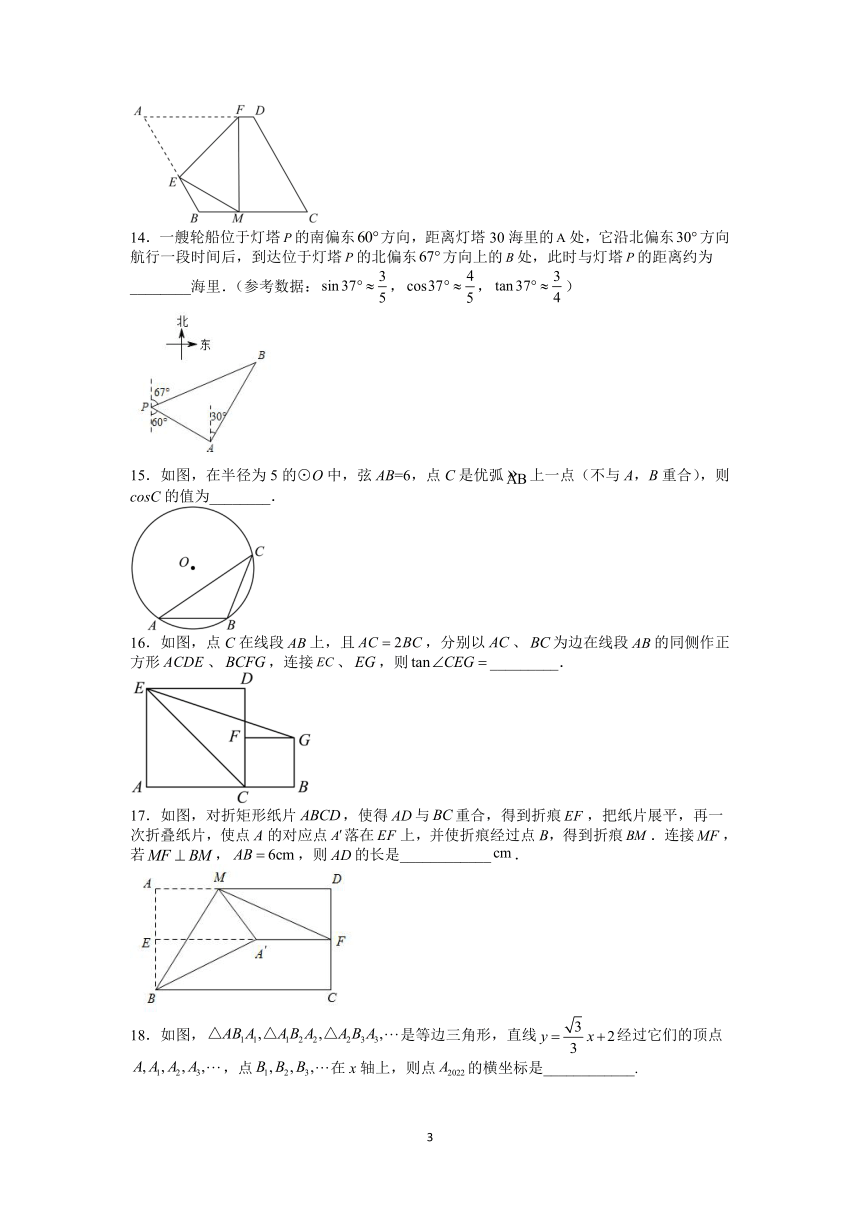
1.计算的值为( )
A. B.0 C. D.
2.在中,,则的值是( ).
A. B. C. D.
3.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
A. B. C. D.1
4.如图,是的高,若,,则边的长为( )
A. B. C. D.
5.如图,在中,.边在轴上,顶点的坐标分别为和.将正方形沿轴向右平移当点落在边上时,点的坐标为( )
A. B. C. D.
6.如图,甲、乙为两座建筑物,它们之间的水平距离为,在A点测得D点的仰角为,在B点测得D点的仰角为,则乙建筑物的高度为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠C=90°,AB=6,AC=2,CD⊥AB于D,设∠ACD=α,则cosα的值为( )
A. B. C. D.
8.在中,若,都是锐角,且,,则的形状是( )
A.钝角三角形 B.等腰三角形 C.锐角三角形 D.直角三角形
9.如图,在中,,,,将绕点A逆时针旋转得到,使点落在AB边上,连结,则的值为( )
A. B. C. D.
10.如图⊙O的直径垂直于弦,垂足是,,,的长为( )
A. B.4 C. D.8
二、填空题(本大题共8小题,在横线上填上合理的答案)
11.计算:(π﹣3)0+(﹣)﹣2﹣4sin30°=___.
12.如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=___________.
13.如图,在菱形ABCD中,∠A=60°,AB=6.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M与点B重合时,EF的长为________;当点M的位置变化时,DF长的最大值为________.
14.一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为________海里.(参考数据:,,)
15.如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为________.
16.如图,点C在线段上,且,分别以、为边在线段的同侧作正方形、,连接、,则_________.
17.如图,对折矩形纸片,使得与重合,得到折痕,把纸片展平,再一次折叠纸片,使点A的对应点落在上,并使折痕经过点B,得到折痕.连接,若,,则的长是____________.
18.如图,是等边三角形,直线经过它们的顶点,点在x轴上,则点的横坐标是____________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
19.计算:
(1)3tan30°+cos245°-2sin60°; (2)-cos30°+sin45°.
20.已知:如图在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,.求:
(1)线段DC的长;
(2)tan∠EDC的值.
21.如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果保留根号)
22.小明学了《解直角三角形》内容后,对一条东西走向的隧道进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东方向上,他沿西北方向前进米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西方向上,(点A、B、C、D在同一平面内)
(1)求点D与点A的距离;
(2)求隧道的长度.(结果保留根号)
23.如图,已知四边形ABCD为矩形,,点E在BC上,,将△ABC沿AC翻折到△AFC,连接EF.
(1)求EF的长;
(2)求sin∠CEF的值.
答案:
1.C 2.C 3.B 4.D 5.B 6.B 7.A 8.D 9.C 10.C 11.3 12.105°.
13. 14.50 15. 16. 17. 18.
19.(1)原式=3×+2-2×=.
(2)原式=-×+×=0.
20.(1)解:在△ABC中,∵AD是边BC上的高,
∴AD⊥BC.
∴.
∵AD=12,
∴.
在Rt△ABD中,∵,
∴CD=BC﹣BD=14﹣9=5.
(2)解:在Rt△ADC中,E是AC的中点,
∴DE=EC,
∴∠EDC=∠C.
∴==.
21.如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.
则DE=BF=CH=10m,
在中,∵AF=80m 10m=70m,
∴DF=AF=70m.
在中,∵DE=10m,
∴
∴
答:障碍物B,C两点间的距离为
22.(1)由题意可知:,
在中,
∴(米)
答:点D与点A的距离为300米.
(2)过点D作于点E.
∵是东西走向
∴
在中,
∴
在中,
∴
∴(米)
答:隧道的长为米
23.(1)设,则,
∴,
在中,,
∴,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
由折叠可知,
∴,,
∴,
∴,
在中,.
(2)过F作FM⊥BC于M,
∴∠FME=∠FMC=90°,
设EM=a,则EC=3-a,
在中, ,
在中,,
∴,
∴,
∴,
∴,
∴,
∴ .
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.计算的值为( )
A. B.0 C. D.
2.在中,,则的值是( ).
A. B. C. D.
3.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
A. B. C. D.1
4.如图,是的高,若,,则边的长为( )
A. B. C. D.
5.如图,在中,.边在轴上,顶点的坐标分别为和.将正方形沿轴向右平移当点落在边上时,点的坐标为( )
A. B. C. D.
6.如图,甲、乙为两座建筑物,它们之间的水平距离为,在A点测得D点的仰角为,在B点测得D点的仰角为,则乙建筑物的高度为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠C=90°,AB=6,AC=2,CD⊥AB于D,设∠ACD=α,则cosα的值为( )
A. B. C. D.
8.在中,若,都是锐角,且,,则的形状是( )
A.钝角三角形 B.等腰三角形 C.锐角三角形 D.直角三角形
9.如图,在中,,,,将绕点A逆时针旋转得到,使点落在AB边上,连结,则的值为( )
A. B. C. D.
10.如图⊙O的直径垂直于弦,垂足是,,,的长为( )
A. B.4 C. D.8
二、填空题(本大题共8小题,在横线上填上合理的答案)
11.计算:(π﹣3)0+(﹣)﹣2﹣4sin30°=___.
12.如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=___________.
13.如图,在菱形ABCD中,∠A=60°,AB=6.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M与点B重合时,EF的长为________;当点M的位置变化时,DF长的最大值为________.
14.一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为________海里.(参考数据:,,)
15.如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为________.
16.如图,点C在线段上,且,分别以、为边在线段的同侧作正方形、,连接、,则_________.
17.如图,对折矩形纸片,使得与重合,得到折痕,把纸片展平,再一次折叠纸片,使点A的对应点落在上,并使折痕经过点B,得到折痕.连接,若,,则的长是____________.
18.如图,是等边三角形,直线经过它们的顶点,点在x轴上,则点的横坐标是____________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
19.计算:
(1)3tan30°+cos245°-2sin60°; (2)-cos30°+sin45°.
20.已知:如图在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,.求:
(1)线段DC的长;
(2)tan∠EDC的值.
21.如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果保留根号)
22.小明学了《解直角三角形》内容后,对一条东西走向的隧道进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东方向上,他沿西北方向前进米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西方向上,(点A、B、C、D在同一平面内)
(1)求点D与点A的距离;
(2)求隧道的长度.(结果保留根号)
23.如图,已知四边形ABCD为矩形,,点E在BC上,,将△ABC沿AC翻折到△AFC,连接EF.
(1)求EF的长;
(2)求sin∠CEF的值.
答案:
1.C 2.C 3.B 4.D 5.B 6.B 7.A 8.D 9.C 10.C 11.3 12.105°.
13. 14.50 15. 16. 17. 18.
19.(1)原式=3×+2-2×=.
(2)原式=-×+×=0.
20.(1)解:在△ABC中,∵AD是边BC上的高,
∴AD⊥BC.
∴.
∵AD=12,
∴.
在Rt△ABD中,∵,
∴CD=BC﹣BD=14﹣9=5.
(2)解:在Rt△ADC中,E是AC的中点,
∴DE=EC,
∴∠EDC=∠C.
∴==.
21.如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.
则DE=BF=CH=10m,
在中,∵AF=80m 10m=70m,
∴DF=AF=70m.
在中,∵DE=10m,
∴
∴
答:障碍物B,C两点间的距离为
22.(1)由题意可知:,
在中,
∴(米)
答:点D与点A的距离为300米.
(2)过点D作于点E.
∵是东西走向
∴
在中,
∴
在中,
∴
∴(米)
答:隧道的长为米
23.(1)设,则,
∴,
在中,,
∴,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
由折叠可知,
∴,,
∴,
∴,
在中,.
(2)过F作FM⊥BC于M,
∴∠FME=∠FMC=90°,
设EM=a,则EC=3-a,
在中, ,
在中,,
∴,
∴,
∴,
∴,
∴,
∴ .
同课章节目录
