九年级下(辽宁省大连市中山区)
图片预览
文档简介
来源于:优雅的夏日,邮箱:herewave@
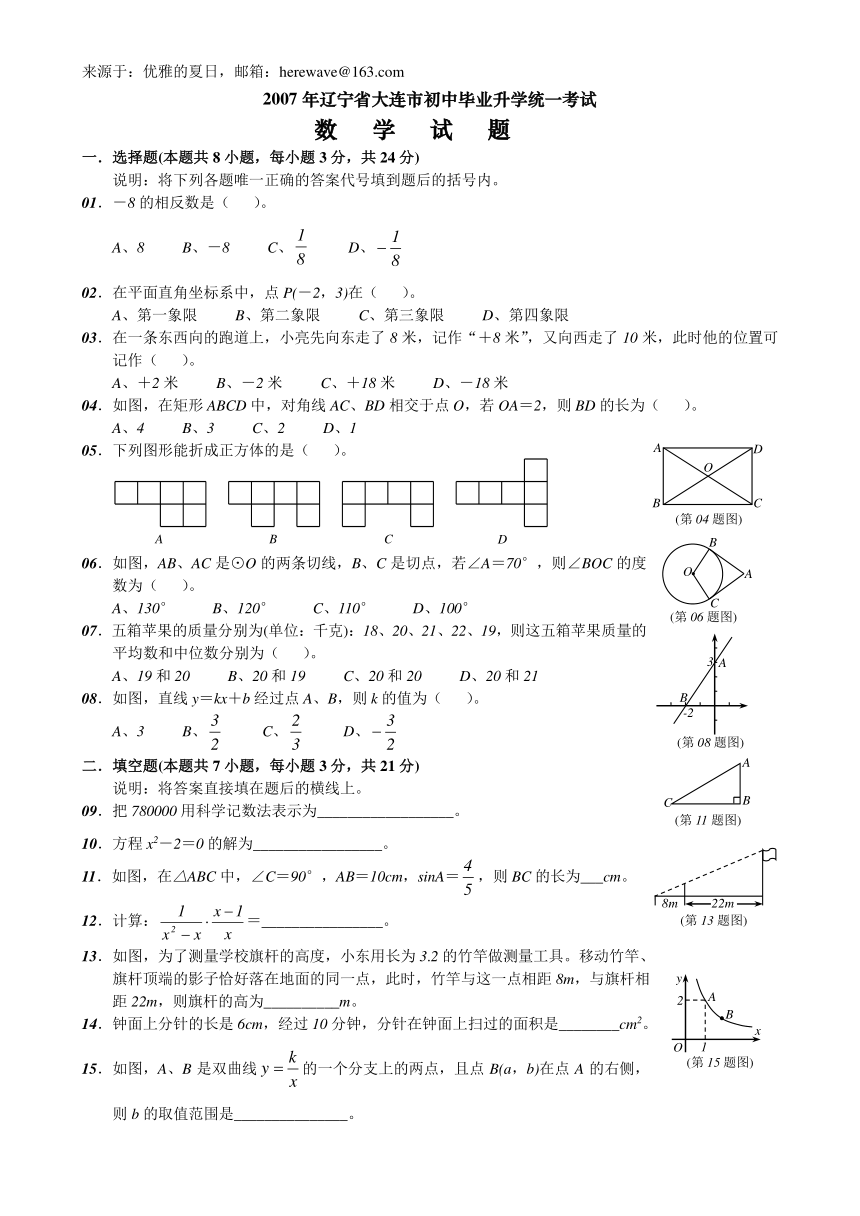
2007年辽宁省大连市初中毕业升学统一考试
数学试题
一.选择题(本题共8小题,每小题3分,共24分)
说明:将下列各题唯一正确的答案代号填到题后的括号内。
01.-8的相反数是( )。
A、8 B、-8 C、 D、
02.在平面直角坐标系中,点P(-2,3)在( )。
A、第一象限 B、第二象限 C、第三象限 D、第四象限
03.在一条东西向的跑道上,小亮先向东走了8米,记作“+8米”,又向西走了10米,此时他的位置可记作( )。
A、+2米 B、-2米 C、+18米 D、-18米
04.如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为( )。
A、4 B、3 C、2 D、1
05.下列图形能折成正方体的是( )。
06.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为( )。
A、130° B、120° C、110° D、100°
07.五箱苹果的质量分别为(单位:千克):18、20、21、22、19,则这五箱苹果质量的平均数和中位数分别为( )。
A、19和20 B、20和19 C、20和20 D、20和21
08.如图,直线y=kx+b经过点A、B,则k的值为( )。
A、3 B、 C、 D、
二.填空题(本题共7小题,每小题3分,共21分)
说明:将答案直接填在题后的横线上。
09.把780000用科学记数法表示为__________________。
10.方程x2-2=0的解为_________________。
11.如图,在△ABC中,∠C=90°,AB=10cm,sinA=,则BC的长为___cm。
12.计算:=________________。
13.如图,为了测量学校旗杆的高度,小东用长为3.2的竹竿做测量工具。移动竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为__________m。
14.钟面上分针的长是6cm,经过10分钟,分针在钟面上扫过的面积是________cm2。
15.如图,A、B是双曲线的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是_______________。
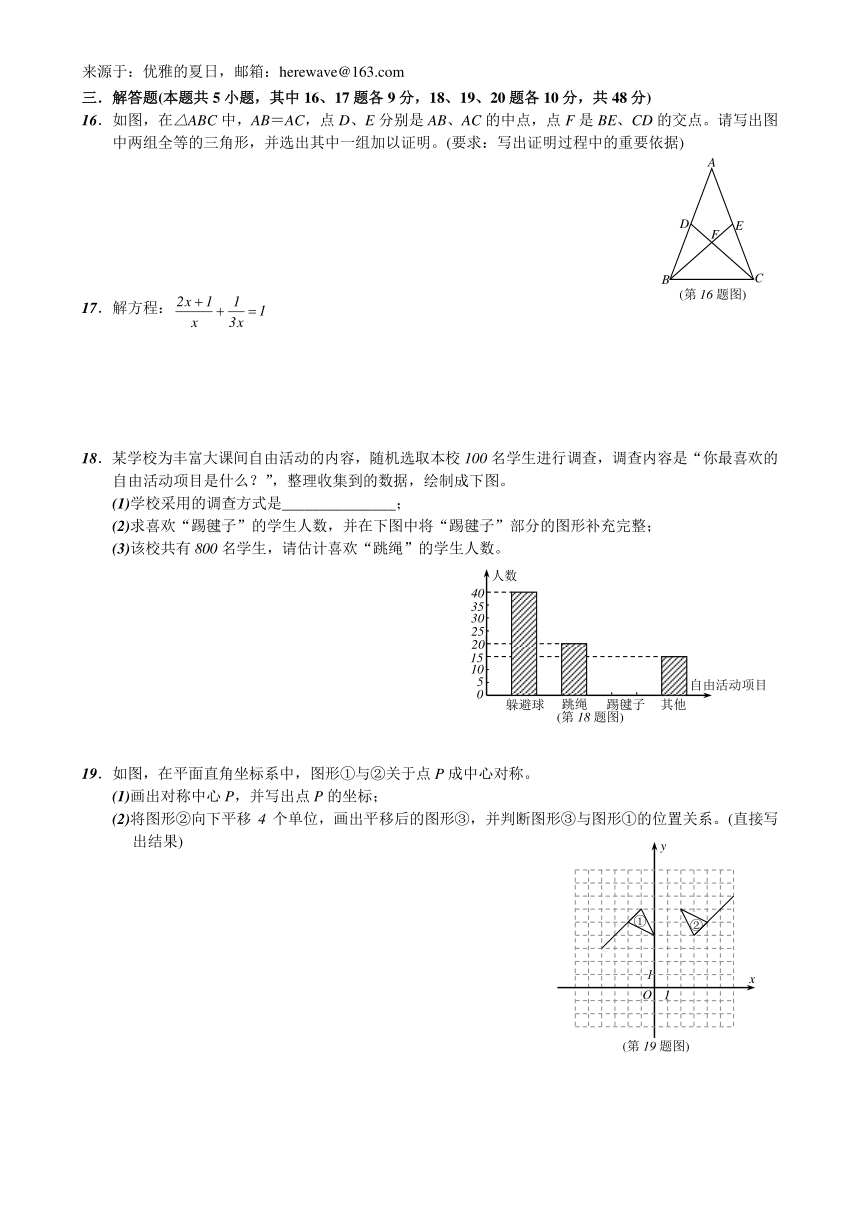
三.解答题(本题共5小题,其中16、17题各9分,18、19、20题各10分,共48分)
16.如图,在△ABC中,AB=AC,点D、E分别是AB、AC的中点,点F是BE、CD的交点。请写出图中两组全等的三角形,并选出其中一组加以证明。(要求:写出证明过程中的重要依据)
17.解方程:
18.某学校为丰富大课间自由活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么?”,整理收集到的数据,绘制成下图。
(1)学校采用的调查方式是_______________;
(2)求喜欢“踢毽子”的学生人数,并在下图中将“踢毽子”部分的图形补充完整;
(3)该校共有800名学生,请估计喜欢“跳绳”的学生人数。
19.如图,在平面直角坐标系中,图形①与②关于点P成中心对称。
(1)画出对称中心P,并写出点P的坐标;
(2)将图形②向下平移4个单位,画出平移后的图形③,并判断图形③与图形①的位置关系。(直接写出结果)
20.为丰富学生的校园文化生活,振兴中学举办了一次学生才艺比赛,三个年级都有男、女各一名选手进入决赛,初一年级选手编号为男1号、女1号,初二年级选手编号为男2号、女2号,初三年级选手编号为男3号、女3号。比赛规则是男、女各一名选手组成搭档展示才艺。
(1)用列举法说明所有可能出现搭档的结果;
(2)求同一年级男、女选手组成搭档的概率;
(3)求高年级男选手与低年级女选手组成搭档的概率。
四.解答题(本题共3小题,其中21、22题各8分,23题7分,共23分)
21.星期天,小强骑自行车到郊外与同学一起游玩,从家出发2小时到达目的地,游玩3小时后按原路以原速返回,小强离家4小时40分钟后,妈妈驾车沿相同路线迎接小强,如图,是他们离家的路程y(千米)与时间x(时)的函数图像。已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时。
(1)小强家与游玩地的距离是多少?
(2)妈妈出发多长时间与小强相遇?
22.某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元。若2元的奖品购买a件。
(1)用含a的代数式表示另外两种奖品的件数;
(2)请你设计购买方案,并说明理由。
23.如图①,小明在研究正方形ABCD的有关问题时,得出:“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,那么EF⊥AE”。他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其它条件不变,发现仍然有“EF⊥AE”结论。
你同意小明的观点吗?若同意,请结合图④加以证明;若不同意,请说明理由。
五.解答题和附加题(解答题共3小题,其中24、25题各12分,26题10分,共34分;附加题5分,但全卷累计得分不超过150分。附加题较难,建议考生最后答附加题)
24.已知抛物线y=ax2+x+2。
(1)当a=-1时,求此抛物线的顶点坐标和对称轴;
(2)若代数式-x2+x+2的值为正整数,求x的值;
(3)当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点M(m,0);当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点N(n,0)。若点M在点N的左边,试比较a1与a2的大小。
25.两个全等的Rt△ABC和Rt△EDA如图放置,点B、A、D在同一条直线上。
操作:在图中,作∠ABC的平分线BF,过点D作DF⊥BF,垂足为F,连结CE。
探究:线段BF、CE的关系,并证明你的结论。
说明:如果你无法证明探究所得的结论,可以将“两个全等的Rt△ABC和Rt△EDA”改为“两个全等的等腰直角△ABC和等腰直角△EDA(点C、A、E在同一条直线上)”,其他条件不变,完成你的证明,此证明过程最多得2分。
26.如图,直线AB交x轴于点A(2,0),交抛物线y=ax2于点B(1,),点C到△OAB各顶点的距离相等,直线AC交y轴于点D。当x>0时,在直线OC和抛物线y=ax2上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,求点P、Q的坐标;若不存在,说明理由。
附加题:在26题中,抛物线的解析式和点D的坐标不变(如图)。当x>0时,在直线y=kx(0<k<1)和这条抛物线上,是否分别存在点P和点Q,使四边形DOPQ为以OD为底的等腰梯形。若存在,求点P、Q的坐标;若不存在,说明理由。
说明
在此,首先对扫描卷的制作者表示感谢。
由于本人水平有限,编辑过程中难免出错,如有错落,请大家见谅并对照扫描卷自行更正。
强烈鄙视转发此卷不注明出处、改头换面剥夺他人劳动成果的某些网站和个人。
天门市卢家口中学 Herewave
2007.07.07
QQ:23271156
MSN:herewave@msn.com
Email:herewave@
A
B
C
D
O
(第04题图)
A
B
C
D
A
(第06题图)
B
C
O
A
B
-2
3
(第08题图)
A
(第11题图)
B
C
8m
22m
(第13题图)
A
(第15题图)
B
1
2
O
x
y
A
(第16题图)
B
C
D
E
F
5
10
15
20
人数
30
25
40
35
0
跳绳
躲避球
踢毽子
其他
(第18题图)
自由活动项目
1
(第19题图)
1
O
x
y
①
②
(第21题图)
O
2
5
C
B
A
D
x(时)
y(千米)
(第23题图)
A
A
A
A
B
B
B
B
C
C
C
C
D
D
E
D
D
E
E
E
F
F
F
F
图①
图②
图③
图④
(第25题图)
A
B
C
D
E
(第26题图)
A
B
C
D
O
x
y
(附加题图)
D
O
x
y
2007年辽宁省大连市初中毕业升学统一考试
数学试题
一.选择题(本题共8小题,每小题3分,共24分)
说明:将下列各题唯一正确的答案代号填到题后的括号内。
01.-8的相反数是( )。
A、8 B、-8 C、 D、
02.在平面直角坐标系中,点P(-2,3)在( )。
A、第一象限 B、第二象限 C、第三象限 D、第四象限
03.在一条东西向的跑道上,小亮先向东走了8米,记作“+8米”,又向西走了10米,此时他的位置可记作( )。
A、+2米 B、-2米 C、+18米 D、-18米
04.如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为( )。
A、4 B、3 C、2 D、1
05.下列图形能折成正方体的是( )。
06.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为( )。
A、130° B、120° C、110° D、100°
07.五箱苹果的质量分别为(单位:千克):18、20、21、22、19,则这五箱苹果质量的平均数和中位数分别为( )。
A、19和20 B、20和19 C、20和20 D、20和21
08.如图,直线y=kx+b经过点A、B,则k的值为( )。
A、3 B、 C、 D、
二.填空题(本题共7小题,每小题3分,共21分)
说明:将答案直接填在题后的横线上。
09.把780000用科学记数法表示为__________________。
10.方程x2-2=0的解为_________________。
11.如图,在△ABC中,∠C=90°,AB=10cm,sinA=,则BC的长为___cm。
12.计算:=________________。
13.如图,为了测量学校旗杆的高度,小东用长为3.2的竹竿做测量工具。移动竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为__________m。
14.钟面上分针的长是6cm,经过10分钟,分针在钟面上扫过的面积是________cm2。
15.如图,A、B是双曲线的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是_______________。
三.解答题(本题共5小题,其中16、17题各9分,18、19、20题各10分,共48分)
16.如图,在△ABC中,AB=AC,点D、E分别是AB、AC的中点,点F是BE、CD的交点。请写出图中两组全等的三角形,并选出其中一组加以证明。(要求:写出证明过程中的重要依据)
17.解方程:
18.某学校为丰富大课间自由活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么?”,整理收集到的数据,绘制成下图。
(1)学校采用的调查方式是_______________;
(2)求喜欢“踢毽子”的学生人数,并在下图中将“踢毽子”部分的图形补充完整;
(3)该校共有800名学生,请估计喜欢“跳绳”的学生人数。
19.如图,在平面直角坐标系中,图形①与②关于点P成中心对称。
(1)画出对称中心P,并写出点P的坐标;
(2)将图形②向下平移4个单位,画出平移后的图形③,并判断图形③与图形①的位置关系。(直接写出结果)
20.为丰富学生的校园文化生活,振兴中学举办了一次学生才艺比赛,三个年级都有男、女各一名选手进入决赛,初一年级选手编号为男1号、女1号,初二年级选手编号为男2号、女2号,初三年级选手编号为男3号、女3号。比赛规则是男、女各一名选手组成搭档展示才艺。
(1)用列举法说明所有可能出现搭档的结果;
(2)求同一年级男、女选手组成搭档的概率;
(3)求高年级男选手与低年级女选手组成搭档的概率。
四.解答题(本题共3小题,其中21、22题各8分,23题7分,共23分)
21.星期天,小强骑自行车到郊外与同学一起游玩,从家出发2小时到达目的地,游玩3小时后按原路以原速返回,小强离家4小时40分钟后,妈妈驾车沿相同路线迎接小强,如图,是他们离家的路程y(千米)与时间x(时)的函数图像。已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时。
(1)小强家与游玩地的距离是多少?
(2)妈妈出发多长时间与小强相遇?
22.某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元。若2元的奖品购买a件。
(1)用含a的代数式表示另外两种奖品的件数;
(2)请你设计购买方案,并说明理由。
23.如图①,小明在研究正方形ABCD的有关问题时,得出:“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,那么EF⊥AE”。他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其它条件不变,发现仍然有“EF⊥AE”结论。
你同意小明的观点吗?若同意,请结合图④加以证明;若不同意,请说明理由。
五.解答题和附加题(解答题共3小题,其中24、25题各12分,26题10分,共34分;附加题5分,但全卷累计得分不超过150分。附加题较难,建议考生最后答附加题)
24.已知抛物线y=ax2+x+2。
(1)当a=-1时,求此抛物线的顶点坐标和对称轴;
(2)若代数式-x2+x+2的值为正整数,求x的值;
(3)当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点M(m,0);当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点N(n,0)。若点M在点N的左边,试比较a1与a2的大小。
25.两个全等的Rt△ABC和Rt△EDA如图放置,点B、A、D在同一条直线上。
操作:在图中,作∠ABC的平分线BF,过点D作DF⊥BF,垂足为F,连结CE。
探究:线段BF、CE的关系,并证明你的结论。
说明:如果你无法证明探究所得的结论,可以将“两个全等的Rt△ABC和Rt△EDA”改为“两个全等的等腰直角△ABC和等腰直角△EDA(点C、A、E在同一条直线上)”,其他条件不变,完成你的证明,此证明过程最多得2分。
26.如图,直线AB交x轴于点A(2,0),交抛物线y=ax2于点B(1,),点C到△OAB各顶点的距离相等,直线AC交y轴于点D。当x>0时,在直线OC和抛物线y=ax2上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,求点P、Q的坐标;若不存在,说明理由。
附加题:在26题中,抛物线的解析式和点D的坐标不变(如图)。当x>0时,在直线y=kx(0<k<1)和这条抛物线上,是否分别存在点P和点Q,使四边形DOPQ为以OD为底的等腰梯形。若存在,求点P、Q的坐标;若不存在,说明理由。
说明
在此,首先对扫描卷的制作者表示感谢。
由于本人水平有限,编辑过程中难免出错,如有错落,请大家见谅并对照扫描卷自行更正。
强烈鄙视转发此卷不注明出处、改头换面剥夺他人劳动成果的某些网站和个人。
天门市卢家口中学 Herewave
2007.07.07
QQ:23271156
MSN:herewave@msn.com
Email:herewave@
A
B
C
D
O
(第04题图)
A
B
C
D
A
(第06题图)
B
C
O
A
B
-2
3
(第08题图)
A
(第11题图)
B
C
8m
22m
(第13题图)
A
(第15题图)
B
1
2
O
x
y
A
(第16题图)
B
C
D
E
F
5
10
15
20
人数
30
25
40
35
0
跳绳
躲避球
踢毽子
其他
(第18题图)
自由活动项目
1
(第19题图)
1
O
x
y
①
②
(第21题图)
O
2
5
C
B
A
D
x(时)
y(千米)
(第23题图)
A
A
A
A
B
B
B
B
C
C
C
C
D
D
E
D
D
E
E
E
F
F
F
F
图①
图②
图③
图④
(第25题图)
A
B
C
D
E
(第26题图)
A
B
C
D
O
x
y
(附加题图)
D
O
x
y
同课章节目录
