三角函数模型的简单应用(广东省东莞市)
文档属性
| 名称 | 三角函数模型的简单应用(广东省东莞市) |  | |
| 格式 | rar | ||
| 文件大小 | 80.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-08-31 19:08:00 | ||
图片预览



文档简介
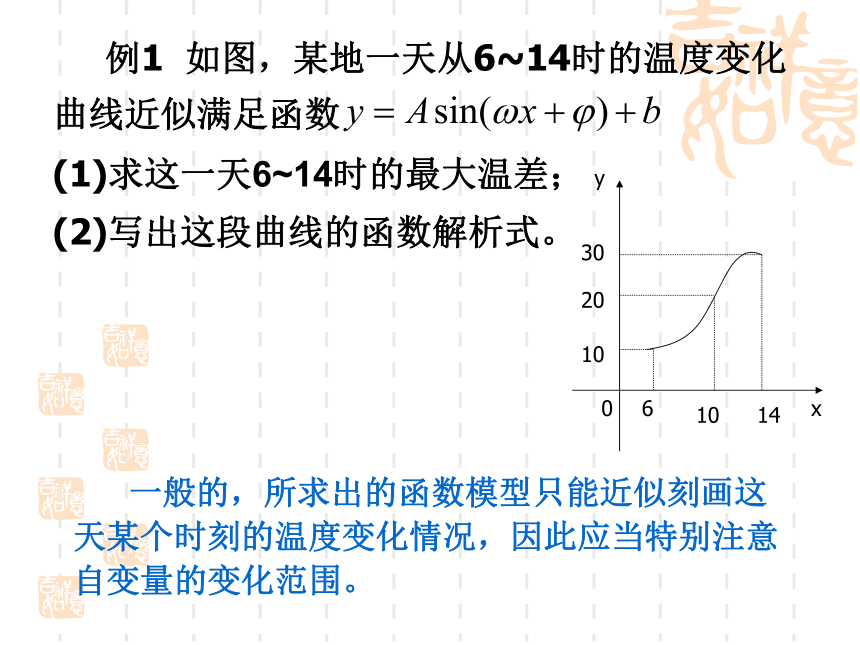
课件16张PPT。1.6 三角函数模型的简单应用 例1 如图,某地一天从6~14时的温度变化曲线近似满足函数
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式。 一般的,所求出的函数模型只能近似刻画这天某个时刻的温度变化情况,因此应当特别注意自变量的变化范围。 练习1:
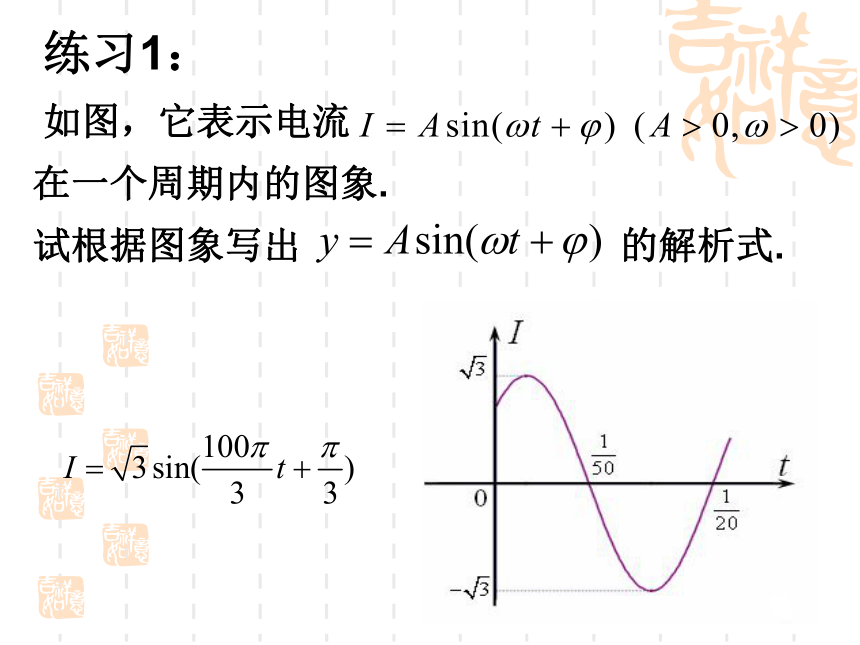
如图,它表示电流 在一个周期内的图象.
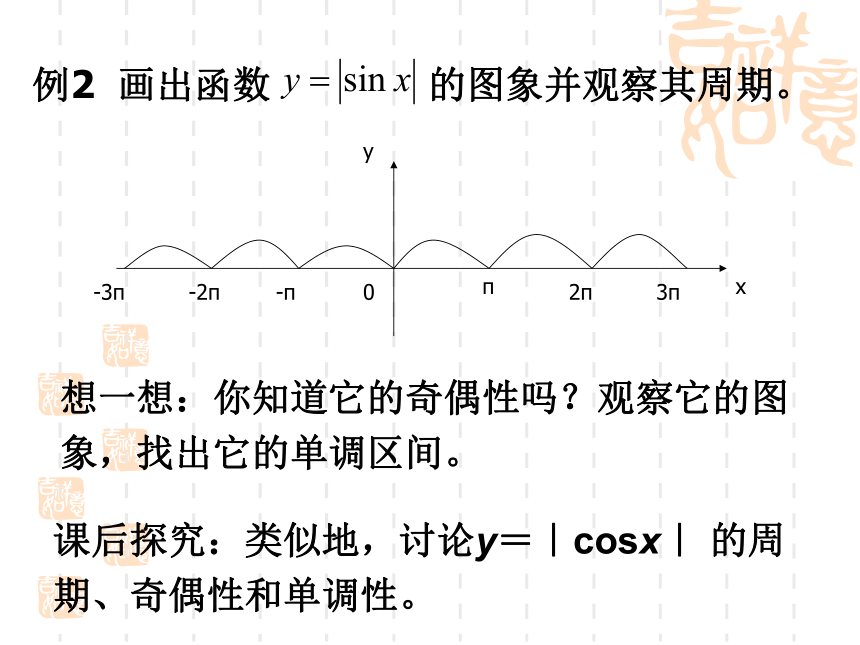
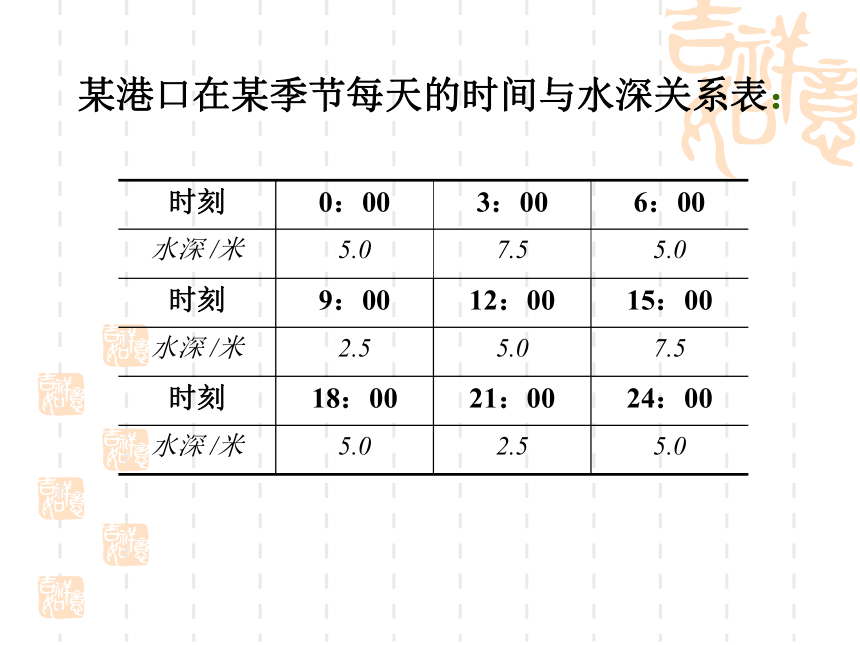
试根据图象写出 的解析式. 思考:例2 画出函数 的图象并观察其周期。想一想:你知道它的奇偶性吗?观察它的图象,找出它的单调区间。课后探究:类似地,讨论y=|cosx| 的周期、奇偶性和单调性。 某港口在某季节每天的时间与水深关系表:思考:
1、上述的变化过程中,哪些量在发生变化?哪个是自变量?哪个是因变量?
2、大约什么时间港口的水最深?深度约是多少?大约什么时间港口的水最浅?深度约是多少?
3、在什么时间范围内,港口的水深增长?在什么时间范围内,港口的水深减少? 4、试着用图形描述这个港口从0时到24时水深的变化情况。
5、用一个函数来近似描述这个港口的水深与时间的函数关系. 课堂练习:五、总结提炼
三角应用题的一般步骤是:
①分析:理解题意,分清已知与未知,画出示意图.
②建模:根据已知条件与求解目标,把已知量与求
解量尽量集中在有关的三角形中,建立一个解三角形的
数学模型.
③求解:利用三角形,求得数学模型的解.
④检验:检验上述所求的解是否符合实际意义,从
而得出实际问题的解.即解三角应用题的基本思路
例3 如图,设地球表面某地正午太阳高度
角为θ,δ为此时太阳直射纬度, 为该地
的纬度值,那么这三个量之间的关系是
当地夏半年δ取正值,
冬半年δ取负值。如果在北京地区(纬度数约为北纬 )
的一幢高为 的楼房北面盖一新楼,要使新
楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离不应小于多少?
所以即在盖楼时,为使后楼不被前楼遮挡,要
留出相当于楼高两倍的间距。解:如图,A、B、C分别为太阳直射北回归线、赤道、南回归线时楼顶在地面上的投影点。要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线的情况考虑,此时的太阳直射纬度为 .依题意两楼的间距应不小于MC.根据太阳高度角的定义,有 实际问题的背景往往比较复杂,而且需要综合应用多学科的知识才能解决它。因此,在应用数学知识解决实际问题时,应当注意从复杂的背景中抽取基本的数学关系,还要调动相关学科知识来帮助理解问题。演示课件作业设计:小结:
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式。 一般的,所求出的函数模型只能近似刻画这天某个时刻的温度变化情况,因此应当特别注意自变量的变化范围。 练习1:
如图,它表示电流 在一个周期内的图象.
试根据图象写出 的解析式. 思考:例2 画出函数 的图象并观察其周期。想一想:你知道它的奇偶性吗?观察它的图象,找出它的单调区间。课后探究:类似地,讨论y=|cosx| 的周期、奇偶性和单调性。 某港口在某季节每天的时间与水深关系表:思考:
1、上述的变化过程中,哪些量在发生变化?哪个是自变量?哪个是因变量?
2、大约什么时间港口的水最深?深度约是多少?大约什么时间港口的水最浅?深度约是多少?
3、在什么时间范围内,港口的水深增长?在什么时间范围内,港口的水深减少? 4、试着用图形描述这个港口从0时到24时水深的变化情况。
5、用一个函数来近似描述这个港口的水深与时间的函数关系. 课堂练习:五、总结提炼
三角应用题的一般步骤是:
①分析:理解题意,分清已知与未知,画出示意图.
②建模:根据已知条件与求解目标,把已知量与求
解量尽量集中在有关的三角形中,建立一个解三角形的
数学模型.
③求解:利用三角形,求得数学模型的解.
④检验:检验上述所求的解是否符合实际意义,从
而得出实际问题的解.即解三角应用题的基本思路
例3 如图,设地球表面某地正午太阳高度
角为θ,δ为此时太阳直射纬度, 为该地
的纬度值,那么这三个量之间的关系是
当地夏半年δ取正值,
冬半年δ取负值。如果在北京地区(纬度数约为北纬 )
的一幢高为 的楼房北面盖一新楼,要使新
楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离不应小于多少?
所以即在盖楼时,为使后楼不被前楼遮挡,要
留出相当于楼高两倍的间距。解:如图,A、B、C分别为太阳直射北回归线、赤道、南回归线时楼顶在地面上的投影点。要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线的情况考虑,此时的太阳直射纬度为 .依题意两楼的间距应不小于MC.根据太阳高度角的定义,有 实际问题的背景往往比较复杂,而且需要综合应用多学科的知识才能解决它。因此,在应用数学知识解决实际问题时,应当注意从复杂的背景中抽取基本的数学关系,还要调动相关学科知识来帮助理解问题。演示课件作业设计:小结:
