2.7正方形课件(共19张PPT) 2022-2023学年湘教版八年级下册数学
文档属性
| 名称 | 2.7正方形课件(共19张PPT) 2022-2023学年湘教版八年级下册数学 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 09:41:34 | ||
图片预览



文档简介
(共19张PPT)
第二章 四边形
2.7 正方形
新课导入
知识要点
思考 正方形跟我们前面学行四边形、矩形、菱形有什么关系?
正方形是特殊的平行四边形.
定义:一组邻边相等且有一个角是直角的平行四边形叫做正方形.
平行四边形不一定是正方形.
知识要点
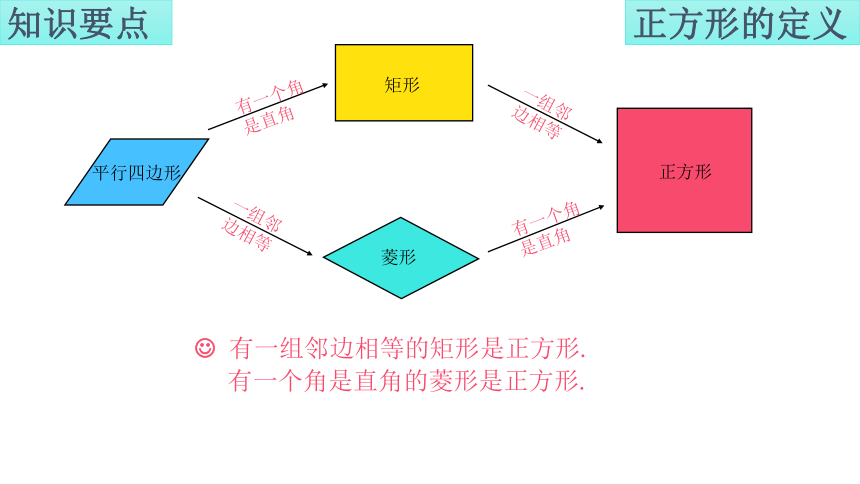
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
平行四边形
菱形
一组邻边相等
有一个角是直角
矩形
有一个角是直角
一组邻边相等
正方形
菱形
正方形的定义
知识要点
平行四边形
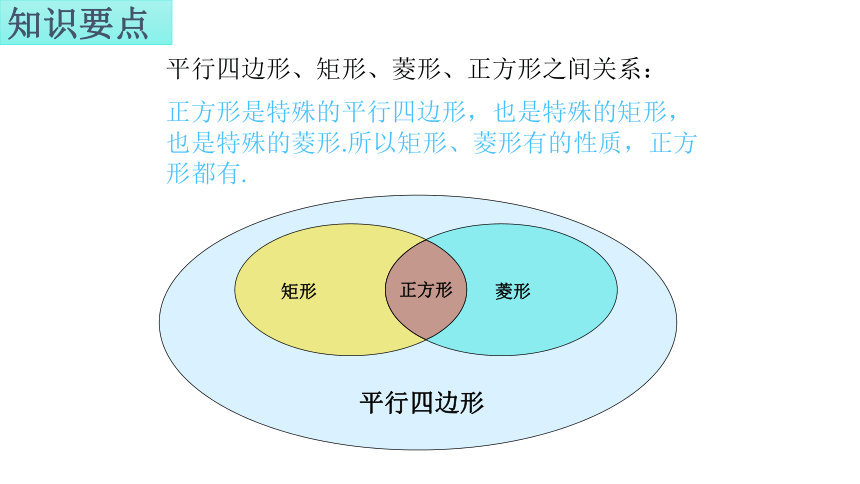
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
矩形
菱形
正方形
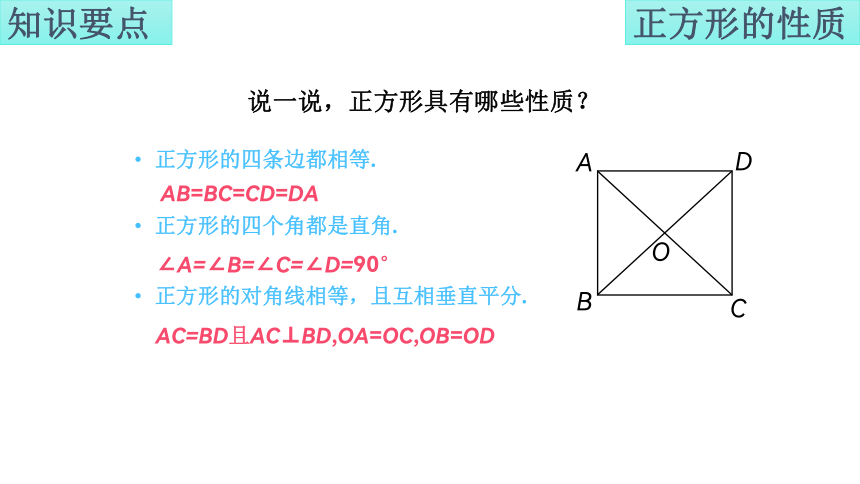
说一说,正方形具有哪些性质?
正方形的四条边都相等.
AB=BC=CD=DA
正方形的四个角都是直角.
∠A=∠B=∠C=∠D=90°
正方形的对角线相等,且互相垂直平分.
AC=BD且AC⊥BD,OA=OC,OB=OD
知识要点
A
B
C
O
D
正方形的性质
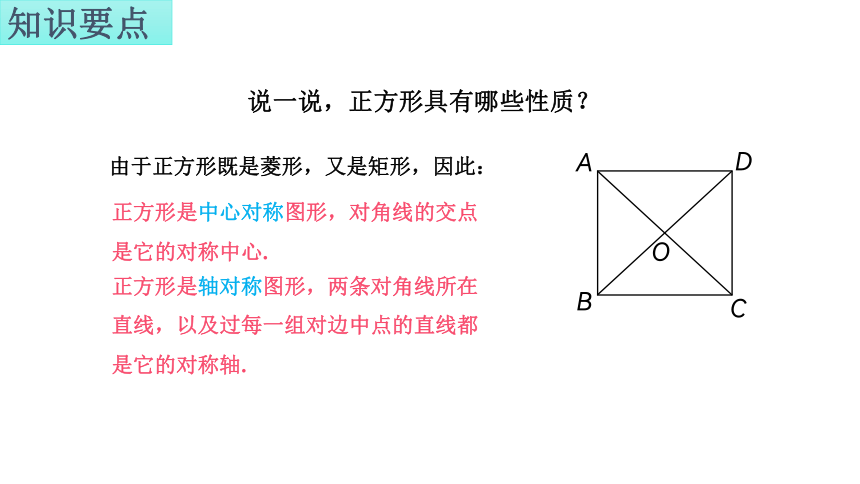
说一说,正方形具有哪些性质?
知识要点
A
B
C
O
D
由于正方形既是菱形,又是矩形,因此:
正方形是中心对称图形,对角线的交点是它的对称中心.
正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴.
典例精析
典例精析
例1 如图,点 E 是正方形 ABCD 的边 AB 上任意一点,过点 D 作 DF⊥DE 交 BC 的延长线于点 F.
求证:DE = DF.
证明:∵四边形 ABCD 为正方形,
∴ AD = CD,∠A = ∠DCF = 90°.
∵ DF⊥ DE,
∴ ∠EDF = 90°,即 ∠1+∠3 = 90°,
又 ∵∠2 +∠3 = 90°,∴∠1 = ∠2.
∴ △AED ≌ △CFD(ASA).
∴ DE = DF.
当堂练习
1.如图,四边形 ABCD 是正方形,对角线 AC 与BD 相交于点 O,AO=2,求正方形的周长与面积.
解:∵四边形 ABCD 是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD 中,由勾股定理,得
AD==2
∴正方形的周长为 4AD= 8 ,
面积为 AD2=8.
A
B
C
O
D
探究新知
说一说,如何判定一个四边形是正方形?
平行四边形
菱形
一组邻边相等
有一个角是直角
矩形
有一个角是直角
一组邻边相等
正方形
菱形
知识要点
正方形的判定方法:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
有一个直角
有一组邻边相等
(或对角线相等)
(或对角线垂直)
平行四边形
正方形
一组邻边相等且
有一个角是直角
正方形的判定
说一说,如何判定一个四边形是正方形?
典例精析
典例精析
例2 如图, 已知点 A′,B′,C′,D′ 分别是正方形 ABCD 四条边上的点,并且 AA′ = BB′ = CC′ = DD′.
求证:四边形 A′B′C′D′ 是正方形.
证明:∵ 四边形 ABCD 为正方形, ∴ AB = BC = CD = DA.
又∵ AA′ = BB′ = CC′ = DD′,∴ D′A = A′B = B′C = C′D.
又∵ ∠A =∠B =∠C =∠D = 90°,
∴ △AA′D′≌△BB′A′≌△CC′B′≌△DD′C′.
∴ A′D′= B′A′= C′B′= D′C′.
∴ 四边形 A′B′C′D′ 是菱形.
又∵ ∠1 =∠3, ∠1 +∠2 = 90°,∴ ∠2 +∠3 = 90°.
∴ ∠D′A′B′= 90°.
∴ 四边形 A′B′C′D′ 是正方形.
当堂练习
2.如图,在Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF是正方形.
证明:∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∠DFC=90°,∠DEC=90°,
又∵∠ACB=90°,
∴四边形DECF是矩形.
∵DE=DF,
∴矩形DECF是正方形.
知识要点
边 角 对角线 对称性
平行四边形
矩形
菱形
正方形
对边平行
且相等
对角相等
两条对角线互相平分
中心对称
对边平行
且相等
四个角
都是直角
两条对角线互相平分且相等
轴对称
中心对称
对边平行,
四条边都相等
对角相等
两条对角线互相垂直平分,
每条对角线平分一组对角
轴对称
中心对称
几种特殊四边形的性质
对边平行,
四条边都相等
四个角
都是直角
两条对角线互相垂直平分且相等, 每条对角线平分一组对角
轴对称
中心对称
特殊四边形的常用判定方法
平行
四边形
(1)两组对边分别平行;
(2)两组对边分别相等;
(3)一组对边
(4)两条对角线互相平分;
(5)两组对角分别相等
矩 形
(1)有三个角是直角;
(2)有一个角是直角的平行四边形;
(3)两条对角线相等的平行四边形
菱 形
(1)四条边都相等;
(2)有一组邻边相等的平行四边形;
(3) 两条对角线互相垂直的平行四边形
正方形
(2)有一组邻边相等的矩形;
(3)有一个角是直角的菱形
平行且相等;
(1)有一个角是直角的有一组邻边相等的平行四边形;
知识要点
当堂练习
3. 平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
4. 一个正方形的对角线长为 2 cm,则它的面积是 ( )
A. 2 cm2 B. 4 cm2 C. 6 cm2 D. 8 cm2
A
当堂练习
5.如图,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
解:(1)∵四边形ABCD为正方形,
∴∠B=90°.
∵EF⊥AC,∴∠EFA=90°.
∵AE平分∠BAC,
∴BE=EF.
又∵AC平分∠BCD,∴∠ACB=45°.
∴∠FEC=∠FCE.∴EF=FC.
∴BE=CF.
当堂练习
5.如图,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
解:(2)设BE=x,则EF=CF=x,
在Rt△CEF中,CE==x
∵BC=1,
∴x+ x=1,
解得x= -1,即BE的长为-1.
课堂小结
正方形
定义:一组邻边相等且有一个角是直角的平行四边形叫做正方形.
性质:正方形的对边平行,四条边都相等,四个角都是直角,对角线相等且互相垂直平分.
正方形是中心对称图形,也是轴对称图形.
判定:一组邻边相等且有一个角是直角的平行四边形叫做正方形.
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
第二章 四边形
2.7 正方形
新课导入
知识要点
思考 正方形跟我们前面学行四边形、矩形、菱形有什么关系?
正方形是特殊的平行四边形.
定义:一组邻边相等且有一个角是直角的平行四边形叫做正方形.
平行四边形不一定是正方形.
知识要点
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
平行四边形
菱形
一组邻边相等
有一个角是直角
矩形
有一个角是直角
一组邻边相等
正方形
菱形
正方形的定义
知识要点
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
矩形
菱形
正方形
说一说,正方形具有哪些性质?
正方形的四条边都相等.
AB=BC=CD=DA
正方形的四个角都是直角.
∠A=∠B=∠C=∠D=90°
正方形的对角线相等,且互相垂直平分.
AC=BD且AC⊥BD,OA=OC,OB=OD
知识要点
A
B
C
O
D
正方形的性质
说一说,正方形具有哪些性质?
知识要点
A
B
C
O
D
由于正方形既是菱形,又是矩形,因此:
正方形是中心对称图形,对角线的交点是它的对称中心.
正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴.
典例精析
典例精析
例1 如图,点 E 是正方形 ABCD 的边 AB 上任意一点,过点 D 作 DF⊥DE 交 BC 的延长线于点 F.
求证:DE = DF.
证明:∵四边形 ABCD 为正方形,
∴ AD = CD,∠A = ∠DCF = 90°.
∵ DF⊥ DE,
∴ ∠EDF = 90°,即 ∠1+∠3 = 90°,
又 ∵∠2 +∠3 = 90°,∴∠1 = ∠2.
∴ △AED ≌ △CFD(ASA).
∴ DE = DF.
当堂练习
1.如图,四边形 ABCD 是正方形,对角线 AC 与BD 相交于点 O,AO=2,求正方形的周长与面积.
解:∵四边形 ABCD 是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD 中,由勾股定理,得
AD==2
∴正方形的周长为 4AD= 8 ,
面积为 AD2=8.
A
B
C
O
D
探究新知
说一说,如何判定一个四边形是正方形?
平行四边形
菱形
一组邻边相等
有一个角是直角
矩形
有一个角是直角
一组邻边相等
正方形
菱形
知识要点
正方形的判定方法:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
有一个直角
有一组邻边相等
(或对角线相等)
(或对角线垂直)
平行四边形
正方形
一组邻边相等且
有一个角是直角
正方形的判定
说一说,如何判定一个四边形是正方形?
典例精析
典例精析
例2 如图, 已知点 A′,B′,C′,D′ 分别是正方形 ABCD 四条边上的点,并且 AA′ = BB′ = CC′ = DD′.
求证:四边形 A′B′C′D′ 是正方形.
证明:∵ 四边形 ABCD 为正方形, ∴ AB = BC = CD = DA.
又∵ AA′ = BB′ = CC′ = DD′,∴ D′A = A′B = B′C = C′D.
又∵ ∠A =∠B =∠C =∠D = 90°,
∴ △AA′D′≌△BB′A′≌△CC′B′≌△DD′C′.
∴ A′D′= B′A′= C′B′= D′C′.
∴ 四边形 A′B′C′D′ 是菱形.
又∵ ∠1 =∠3, ∠1 +∠2 = 90°,∴ ∠2 +∠3 = 90°.
∴ ∠D′A′B′= 90°.
∴ 四边形 A′B′C′D′ 是正方形.
当堂练习
2.如图,在Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF是正方形.
证明:∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∠DFC=90°,∠DEC=90°,
又∵∠ACB=90°,
∴四边形DECF是矩形.
∵DE=DF,
∴矩形DECF是正方形.
知识要点
边 角 对角线 对称性
平行四边形
矩形
菱形
正方形
对边平行
且相等
对角相等
两条对角线互相平分
中心对称
对边平行
且相等
四个角
都是直角
两条对角线互相平分且相等
轴对称
中心对称
对边平行,
四条边都相等
对角相等
两条对角线互相垂直平分,
每条对角线平分一组对角
轴对称
中心对称
几种特殊四边形的性质
对边平行,
四条边都相等
四个角
都是直角
两条对角线互相垂直平分且相等, 每条对角线平分一组对角
轴对称
中心对称
特殊四边形的常用判定方法
平行
四边形
(1)两组对边分别平行;
(2)两组对边分别相等;
(3)一组对边
(4)两条对角线互相平分;
(5)两组对角分别相等
矩 形
(1)有三个角是直角;
(2)有一个角是直角的平行四边形;
(3)两条对角线相等的平行四边形
菱 形
(1)四条边都相等;
(2)有一组邻边相等的平行四边形;
(3) 两条对角线互相垂直的平行四边形
正方形
(2)有一组邻边相等的矩形;
(3)有一个角是直角的菱形
平行且相等;
(1)有一个角是直角的有一组邻边相等的平行四边形;
知识要点
当堂练习
3. 平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
4. 一个正方形的对角线长为 2 cm,则它的面积是 ( )
A. 2 cm2 B. 4 cm2 C. 6 cm2 D. 8 cm2
A
当堂练习
5.如图,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
解:(1)∵四边形ABCD为正方形,
∴∠B=90°.
∵EF⊥AC,∴∠EFA=90°.
∵AE平分∠BAC,
∴BE=EF.
又∵AC平分∠BCD,∴∠ACB=45°.
∴∠FEC=∠FCE.∴EF=FC.
∴BE=CF.
当堂练习
5.如图,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
解:(2)设BE=x,则EF=CF=x,
在Rt△CEF中,CE==x
∵BC=1,
∴x+ x=1,
解得x= -1,即BE的长为-1.
课堂小结
正方形
定义:一组邻边相等且有一个角是直角的平行四边形叫做正方形.
性质:正方形的对边平行,四条边都相等,四个角都是直角,对角线相等且互相垂直平分.
正方形是中心对称图形,也是轴对称图形.
判定:一组邻边相等且有一个角是直角的平行四边形叫做正方形.
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
