9.1.1 认识三角形 学案
图片预览



文档简介
中小学教育资源及组卷应用平台
9.1.1 认识三角形 导学案
课题 9.1.1 认识三角形 单元 第9单元 学科 数学 年级 七年级(下)
教材分析 在小学时,学生已经认识了三角形,在此基础上,来进一步理解三角形的概念,为以后进一步学习多边形及其性质作好铺垫.三角形是学生在生活中常见的图形,学生具备一定的认知能力,对三角形的边、角有关概念的学习不会有更大的障碍,但对外角的认识是一个难点,通过动手画一画、小组合作探究来帮助他们突破难点,从而实现本节课的教学目标.
核心素养分析 让学生通过“感知―概括―应用”的思维过程去发现知识、掌握规律,并通过师生间和生生间的多层次、多通道的主体信息交流,发展学生的逻辑推理能力.
学习目标 1.了解三角形的基本元素与中线、高线、角平分线.2.掌握不同形状的三角形,三角形按角、按边分类的方法.3.知道等腰三角形、等边三角形的概念.
重点 三角形的边和内角,以及外角,等腰三角形、等边三角形的区别和联系.
难点 对外角概念的理解.
教学过程
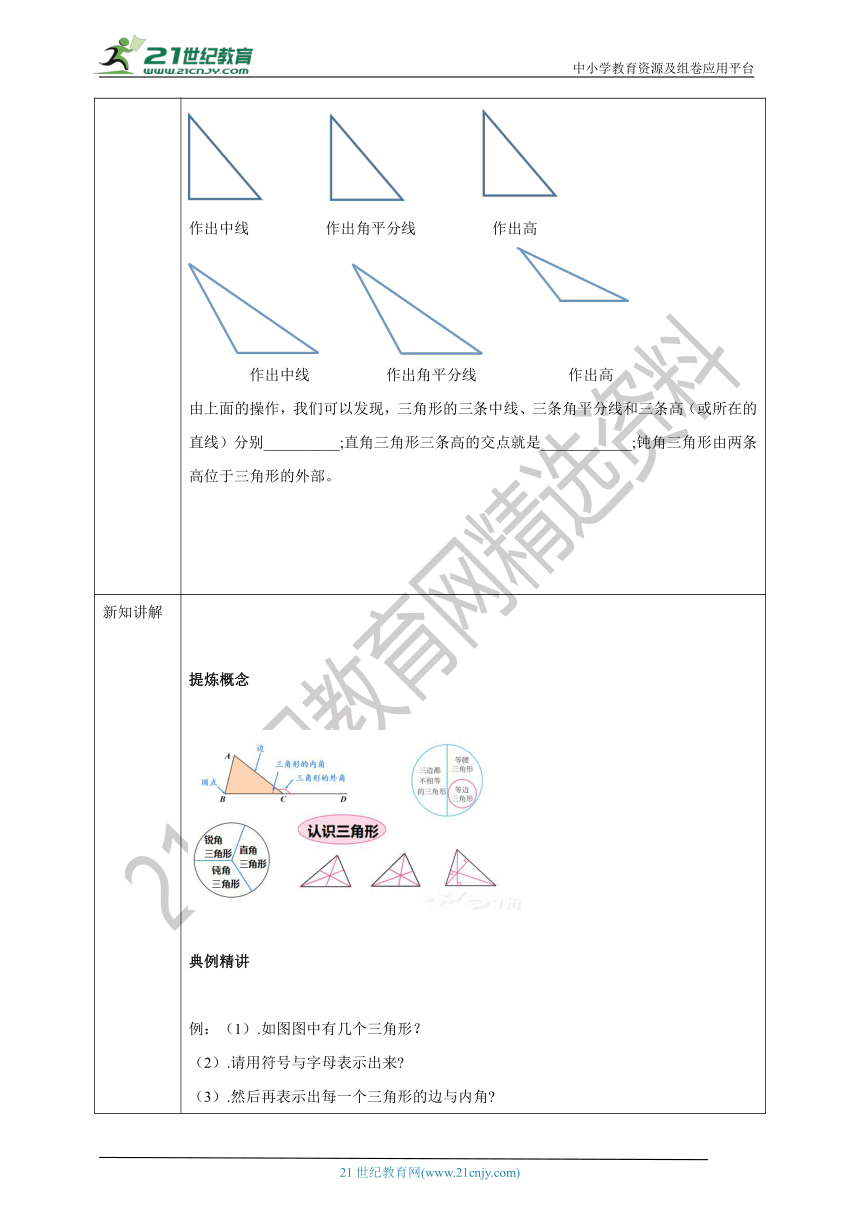
课前预学 引入思考探究一:三角形( triangle)是我们早就认识的几何图形,它是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形,这三条线段就是三角形的边.三角形的顶点采用大写字母A、B、C、…表示,如图9.1.2(1),整个三角形记为△ABC.图9.1.2(1)如图9.1.2(2)所示,在三角形中,每两条边所组成的角叫做三角形的内角,如∠ACB;三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角,如∠ACD是与△ABC的内角∠ACB相邻的外角.思考 △ABC有多少个内角 多少个外角 与内角∠A相邻的外角有几个 它们是什么关系 怎样画出△ABC的外角 探究二:图9.1.3中,三个三角形的内角各有什么特点 (1) (2) (3)第一个三角形中,三个内角均为锐角;第二个三角形中,有一个内角是直角;第三个三角形中,有一个内角是钝角.三角形可以按角来分类:试一试图9.1.4中,三个三角形的边各有什么特点 (1) (2) (3)第一个三角形的三边互不相等;第二个三角形有两条边相等;第三个三角形的三边都相等.我们把有两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形称为等边三角形(或正三角形).三角形可以按边来分类:探究三:如图9.1.6所示,取△ABC边AB的中点E,连结CE,线段CE就是△ABC的一条中线;图9.1.6作△ABC的内角∠BAC的平分线交对边BC于点D,线段AD就是∠ABC的一条角平分线过顶点B作△ABC的边AC的垂线,垂足为点F,线段BF就是△ABC的一条高.做一做下面给出了三个相同的锐角三角形,分别在这三个三角形中画出三条中线、三条角平分线和三条高。作出中线 作出角平分线 作出高把锐角三角形换成直角三角形或钝角三角形,再试一试,你发现了什么?作出中线 作出角平分线 作出高作出中线 作出角平分线 作出高由上面的操作,我们可以发现,三角形的三条中线、三条角平分线和三条高(或所在的直线)分别__________;直角三角形三条高的交点就是____________;钝角三角形由两条高位于三角形的外部。
新知讲解 提炼概念典例精讲 例:(1).如图图中有几个三角形?(2).请用符号与字母表示出来 (3).然后再表示出每一个三角形的边与内角
课堂练习 巩固训练 1.下列说法中错误的是( )A. 等腰三角形可能是钝角三角形B. 等边三角形是等腰三角形C. 等腰三角形一定是锐角三角形D. 等边三角形一定是锐角三角形2. 在下图中,正确画出△ABC 中边 BC 上高的是( )如图所示图中共有____个三角形,其中以BC为边的三角形是__________,∠BEC是________ 的内角,∠1是________的外角.4.三角形的一个内角与它相邻的外角的和为______.5.在图中找出等腰三角形、正三角形、锐角三角形、直角三角形和钝角三角形. 答案引入思考探究一思考三角形有3个内角,6个外角,与内角∠A相邻的外角有2个,它们是互补的。探究二三角形可以按角来分类:所有内角都是锐角——锐角三角形;有一个内角是直角——直角三角形;有一个内角是钝角——钝角三角形.我们把有两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形称为等边三角形(或正三角形).三角形可以按边来分类:提炼概念典例精讲 例(1)3个 (2)△ABC △ADC △ABD(3)(3)△ABC中 边:AB BC CD 内角为∠BAC ∠B ∠C △ADC中 边:AD AC CD 内角为∠DAC ∠ADC ∠C △ABD中 边:AD AB BD 内角为∠BAD ∠B ∠ADB 巩固训练CC4. 180°5. 等腰三角形:△MOH,△HOP,△POK正三角形:△MOH锐角三角形:△MOH,△HOP,△POK直角三角形:△BMH,△PRF,△DEF,△BAC钝角三角形:△PKF,△MFD,△MCD.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
9.1.1 认识三角形 导学案
课题 9.1.1 认识三角形 单元 第9单元 学科 数学 年级 七年级(下)
教材分析 在小学时,学生已经认识了三角形,在此基础上,来进一步理解三角形的概念,为以后进一步学习多边形及其性质作好铺垫.三角形是学生在生活中常见的图形,学生具备一定的认知能力,对三角形的边、角有关概念的学习不会有更大的障碍,但对外角的认识是一个难点,通过动手画一画、小组合作探究来帮助他们突破难点,从而实现本节课的教学目标.
核心素养分析 让学生通过“感知―概括―应用”的思维过程去发现知识、掌握规律,并通过师生间和生生间的多层次、多通道的主体信息交流,发展学生的逻辑推理能力.
学习目标 1.了解三角形的基本元素与中线、高线、角平分线.2.掌握不同形状的三角形,三角形按角、按边分类的方法.3.知道等腰三角形、等边三角形的概念.
重点 三角形的边和内角,以及外角,等腰三角形、等边三角形的区别和联系.
难点 对外角概念的理解.
教学过程
课前预学 引入思考探究一:三角形( triangle)是我们早就认识的几何图形,它是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形,这三条线段就是三角形的边.三角形的顶点采用大写字母A、B、C、…表示,如图9.1.2(1),整个三角形记为△ABC.图9.1.2(1)如图9.1.2(2)所示,在三角形中,每两条边所组成的角叫做三角形的内角,如∠ACB;三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角,如∠ACD是与△ABC的内角∠ACB相邻的外角.思考 △ABC有多少个内角 多少个外角 与内角∠A相邻的外角有几个 它们是什么关系 怎样画出△ABC的外角 探究二:图9.1.3中,三个三角形的内角各有什么特点 (1) (2) (3)第一个三角形中,三个内角均为锐角;第二个三角形中,有一个内角是直角;第三个三角形中,有一个内角是钝角.三角形可以按角来分类:试一试图9.1.4中,三个三角形的边各有什么特点 (1) (2) (3)第一个三角形的三边互不相等;第二个三角形有两条边相等;第三个三角形的三边都相等.我们把有两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形称为等边三角形(或正三角形).三角形可以按边来分类:探究三:如图9.1.6所示,取△ABC边AB的中点E,连结CE,线段CE就是△ABC的一条中线;图9.1.6作△ABC的内角∠BAC的平分线交对边BC于点D,线段AD就是∠ABC的一条角平分线过顶点B作△ABC的边AC的垂线,垂足为点F,线段BF就是△ABC的一条高.做一做下面给出了三个相同的锐角三角形,分别在这三个三角形中画出三条中线、三条角平分线和三条高。作出中线 作出角平分线 作出高把锐角三角形换成直角三角形或钝角三角形,再试一试,你发现了什么?作出中线 作出角平分线 作出高作出中线 作出角平分线 作出高由上面的操作,我们可以发现,三角形的三条中线、三条角平分线和三条高(或所在的直线)分别__________;直角三角形三条高的交点就是____________;钝角三角形由两条高位于三角形的外部。
新知讲解 提炼概念典例精讲 例:(1).如图图中有几个三角形?(2).请用符号与字母表示出来 (3).然后再表示出每一个三角形的边与内角
课堂练习 巩固训练 1.下列说法中错误的是( )A. 等腰三角形可能是钝角三角形B. 等边三角形是等腰三角形C. 等腰三角形一定是锐角三角形D. 等边三角形一定是锐角三角形2. 在下图中,正确画出△ABC 中边 BC 上高的是( )如图所示图中共有____个三角形,其中以BC为边的三角形是__________,∠BEC是________ 的内角,∠1是________的外角.4.三角形的一个内角与它相邻的外角的和为______.5.在图中找出等腰三角形、正三角形、锐角三角形、直角三角形和钝角三角形. 答案引入思考探究一思考三角形有3个内角,6个外角,与内角∠A相邻的外角有2个,它们是互补的。探究二三角形可以按角来分类:所有内角都是锐角——锐角三角形;有一个内角是直角——直角三角形;有一个内角是钝角——钝角三角形.我们把有两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形称为等边三角形(或正三角形).三角形可以按边来分类:提炼概念典例精讲 例(1)3个 (2)△ABC △ADC △ABD(3)(3)△ABC中 边:AB BC CD 内角为∠BAC ∠B ∠C △ADC中 边:AD AC CD 内角为∠DAC ∠ADC ∠C △ABD中 边:AD AB BD 内角为∠BAD ∠B ∠ADB 巩固训练CC4. 180°5. 等腰三角形:△MOH,△HOP,△POK正三角形:△MOH锐角三角形:△MOH,△HOP,△POK直角三角形:△BMH,△PRF,△DEF,△BAC钝角三角形:△PKF,△MFD,△MCD.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
