6.4.3.2正弦定理 课件(共37张PPT)
文档属性
| 名称 | 6.4.3.2正弦定理 课件(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-04 15:21:26 | ||
图片预览









文档简介
(共37张PPT)
6.4.3-2
正 弦 定 理
高一数学必修第二册 第六章 平面向量及其应用
借助向量的运算,探索三角形边长与角度的关系;
2.掌握正弦定理,并能利用正弦定理解三角形、判
断三角形解的个数问题;
3.能利用正弦、余弦定理解决三角形中边与角的关系;
4.掌握正弦、余弦定理的简单应用.
5.核心素养:数学抽象、数学建模、数学运算.
学习目标
黄河壶口瀑布
一.创设问题情境
任务:测量壶口瀑布壶口
处的距离AB.
工具:卷尺,测角仪.
A
B
如何测量呢
余弦定理及其推论分别给出了已知两边及其夹角、
已知三边直接解三角形的公式.如果已知两角和一边,
是否也有相应的直接三角形的公式呢?
二、探究新知
1.思考:
向量是数量积运算中出现了角的余弦,而我们需要
的是角的正弦,如何实现转化?
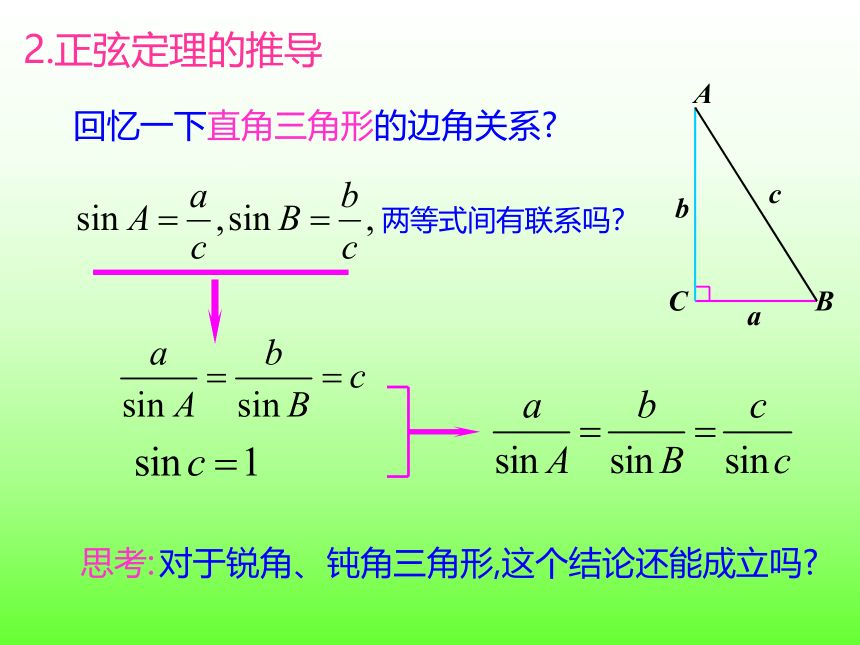
回忆一下直角三角形的边角关系
两等式间有联系吗?
思考:
对于锐角、钝角三角形,这个结论还能成立吗
2.正弦定理的推导
A
B
C
c
b
a
A
B
C
如图,在锐角 时
C
A
B
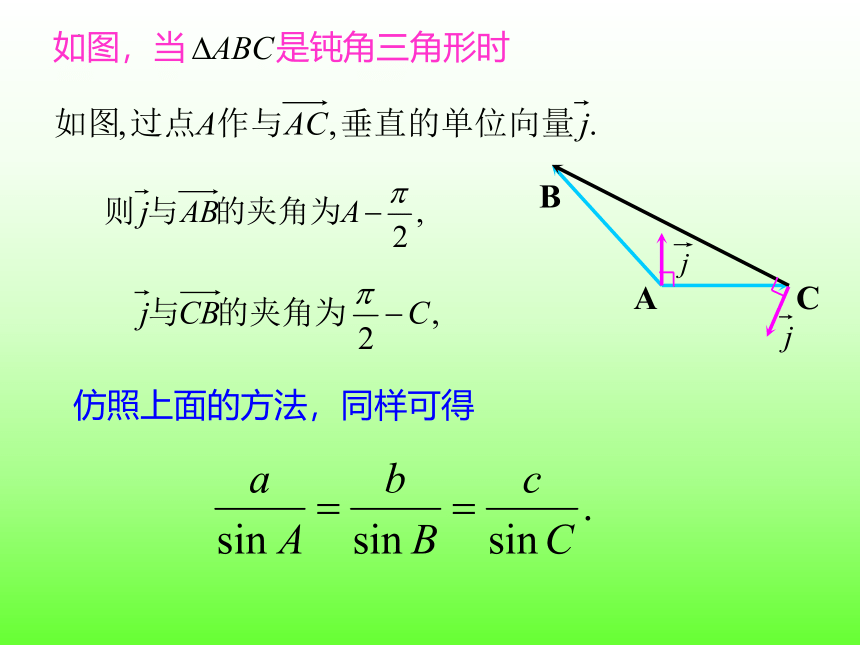
仿照上面的方法,同样可得
如图,当 是钝角三角形时
B
A
C
C1
a
b
c
· O
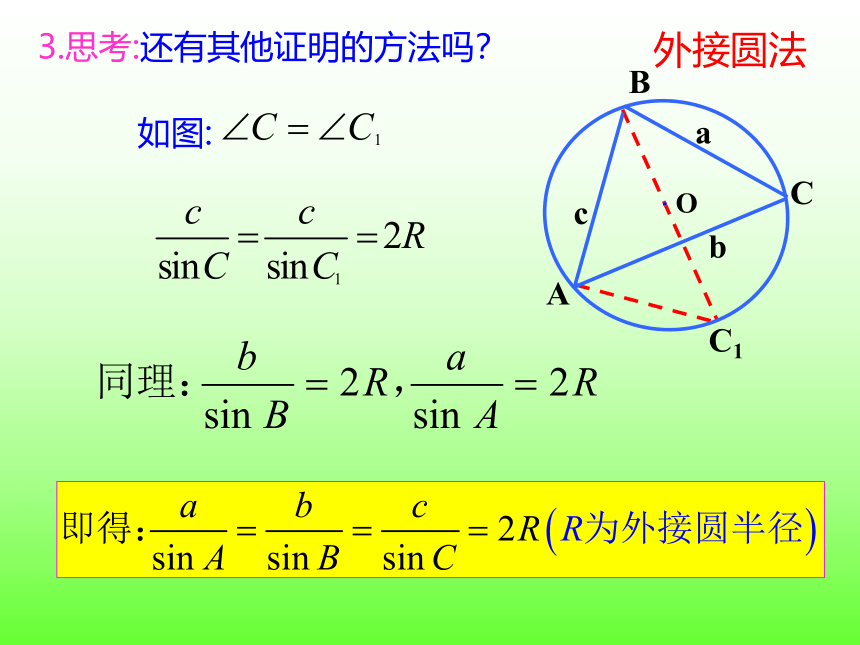
如图:
3.思考:还有其他证明的方法吗?
外接圆法
4.正弦定理:
含三角形的三边及三内角,由己知二角一边
或二边一角可表示其它的边和角.
定理结构特征:
在一个三角形中,各边和它所对角的
正弦的比相等,即
5.剖析定理、加深理解
(1).A+B+C=π.
(2).大角对大边,大边对大角.
2).一般地,把三角形的三个角A,B,C和它们的对边
a,b,c叫做三角形的元素。已知三角形的几个元
素求其他元素的过程叫解三角形
3).正弦定理可以解决三角形中的问题:
(1).已知两边和其中一边的对角,求另一边的对角, 进而
可求其他的边和角
(2).已知两角和一边,求其他角和边
1).
6.正弦定理的变形公式
1).
三、巩固新知
1.例7.
课本p47例7
(1)已知两角和任一边,求其他两边和一角
在△ABC 中,已知c = 10,A = 45。, C = 30。,解三角形.
得
b =
=
=
B
A
C
b
c
a
解:根据三角形内角和定理,
2.变式
(2)已知两边和其中一边的对角,求其它边和角.
(三角形中大边对大角)
3.例8.
课本p47例8
(三角形中大边对大角)
4.变式
5.例9.根据下列条件,判断△ABC的形状.
直角三角形
等腰三角形
直角三角形或等腰三角形
6.变式
7.例10.
8.变式
四、课堂检测
1.本节课你学习了哪些基本知识?
2.本节课你学会了哪些思想方法?
数形结合思想、化归转化思想
五、课堂小结
作业:(1)课本P48 练习 2、3题
(2)做完《一线课堂》对应习题
9.探究:引入时黄河壶口瀑布问题的解决方法
A
B
C
b
c
8
10
5
7
9
8
9
10
(1)
(2)
(3)
(4)
(5)
具备下列哪个条件可以直接使用正弦定理解三角形
6
(6)
已知两角一边,
可求其它边和角!
已知两边一对角,
可求其它边和角!
5.变式训练3
(2),(4),(5)
(1)b=11, a=20, B=30o
(2)c=54, b=39, C=120o
(3)b=26, c=15, C=30o
(4)a=2,b=6,A=30o
两解
一解
两解
无解
6.例3.判断满足下列的三角形的个数:
1).若A为锐角时:
2).若A为直角或钝角时:
7.已知a,b和A用正弦定理求B时的各种情况
无解
8.变式训练4
9.探究:引入时黄河壶口瀑布问题的解决方法
A
B
C
b
c
10.例4.根据下列条件,判断△ABC的形状.
直角三角形
等腰三角形
在△ABC中,已知
试判断△ABC的形状.
直角三角形
或等腰三角形
11.变式训练5
1.
四、课堂小结
2.正弦定理可以解决三角形中的问题:
(1).已知两边和其中一边的对角,求另一边的对角, 进而
可求其他的边和角
(2).已知两角和一边,求其他角和边
3.实现三角形当中边角之间的转化
作业:课本P48 练习 2、3题
七、能力提升
2.△ABC的三个内角A,B,C对应的三边长分别
为a,b,c且满足
①求角C的大小;
②若 求 和b的值.
3.
(4)△ABC的三个内角A,B,C对应三边长分别
为a,b,c且
①求角A的大小;
②若 试判断△ABC的形状.
正三角形
6.4.3-2
正 弦 定 理
高一数学必修第二册 第六章 平面向量及其应用
借助向量的运算,探索三角形边长与角度的关系;
2.掌握正弦定理,并能利用正弦定理解三角形、判
断三角形解的个数问题;
3.能利用正弦、余弦定理解决三角形中边与角的关系;
4.掌握正弦、余弦定理的简单应用.
5.核心素养:数学抽象、数学建模、数学运算.
学习目标
黄河壶口瀑布
一.创设问题情境
任务:测量壶口瀑布壶口
处的距离AB.
工具:卷尺,测角仪.
A
B
如何测量呢
余弦定理及其推论分别给出了已知两边及其夹角、
已知三边直接解三角形的公式.如果已知两角和一边,
是否也有相应的直接三角形的公式呢?
二、探究新知
1.思考:
向量是数量积运算中出现了角的余弦,而我们需要
的是角的正弦,如何实现转化?
回忆一下直角三角形的边角关系
两等式间有联系吗?
思考:
对于锐角、钝角三角形,这个结论还能成立吗
2.正弦定理的推导
A
B
C
c
b
a
A
B
C
如图,在锐角 时
C
A
B
仿照上面的方法,同样可得
如图,当 是钝角三角形时
B
A
C
C1
a
b
c
· O
如图:
3.思考:还有其他证明的方法吗?
外接圆法
4.正弦定理:
含三角形的三边及三内角,由己知二角一边
或二边一角可表示其它的边和角.
定理结构特征:
在一个三角形中,各边和它所对角的
正弦的比相等,即
5.剖析定理、加深理解
(1).A+B+C=π.
(2).大角对大边,大边对大角.
2).一般地,把三角形的三个角A,B,C和它们的对边
a,b,c叫做三角形的元素。已知三角形的几个元
素求其他元素的过程叫解三角形
3).正弦定理可以解决三角形中的问题:
(1).已知两边和其中一边的对角,求另一边的对角, 进而
可求其他的边和角
(2).已知两角和一边,求其他角和边
1).
6.正弦定理的变形公式
1).
三、巩固新知
1.例7.
课本p47例7
(1)已知两角和任一边,求其他两边和一角
在△ABC 中,已知c = 10,A = 45。, C = 30。,解三角形.
得
b =
=
=
B
A
C
b
c
a
解:根据三角形内角和定理,
2.变式
(2)已知两边和其中一边的对角,求其它边和角.
(三角形中大边对大角)
3.例8.
课本p47例8
(三角形中大边对大角)
4.变式
5.例9.根据下列条件,判断△ABC的形状.
直角三角形
等腰三角形
直角三角形或等腰三角形
6.变式
7.例10.
8.变式
四、课堂检测
1.本节课你学习了哪些基本知识?
2.本节课你学会了哪些思想方法?
数形结合思想、化归转化思想
五、课堂小结
作业:(1)课本P48 练习 2、3题
(2)做完《一线课堂》对应习题
9.探究:引入时黄河壶口瀑布问题的解决方法
A
B
C
b
c
8
10
5
7
9
8
9
10
(1)
(2)
(3)
(4)
(5)
具备下列哪个条件可以直接使用正弦定理解三角形
6
(6)
已知两角一边,
可求其它边和角!
已知两边一对角,
可求其它边和角!
5.变式训练3
(2),(4),(5)
(1)b=11, a=20, B=30o
(2)c=54, b=39, C=120o
(3)b=26, c=15, C=30o
(4)a=2,b=6,A=30o
两解
一解
两解
无解
6.例3.判断满足下列的三角形的个数:
1).若A为锐角时:
2).若A为直角或钝角时:
7.已知a,b和A用正弦定理求B时的各种情况
无解
8.变式训练4
9.探究:引入时黄河壶口瀑布问题的解决方法
A
B
C
b
c
10.例4.根据下列条件,判断△ABC的形状.
直角三角形
等腰三角形
在△ABC中,已知
试判断△ABC的形状.
直角三角形
或等腰三角形
11.变式训练5
1.
四、课堂小结
2.正弦定理可以解决三角形中的问题:
(1).已知两边和其中一边的对角,求另一边的对角, 进而
可求其他的边和角
(2).已知两角和一边,求其他角和边
3.实现三角形当中边角之间的转化
作业:课本P48 练习 2、3题
七、能力提升
2.△ABC的三个内角A,B,C对应的三边长分别
为a,b,c且满足
①求角C的大小;
②若 求 和b的值.
3.
(4)△ABC的三个内角A,B,C对应三边长分别
为a,b,c且
①求角A的大小;
②若 试判断△ABC的形状.
正三角形
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
