人教版八年级下册数学第18章平行四边形证明题(无答案)
文档属性
| 名称 | 人教版八年级下册数学第18章平行四边形证明题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 265.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 09:12:59 | ||
图片预览


文档简介
人教版八年级下册数学第18章平行四边形证明题
如图,已知菱形 中,对角线 相交于点 ,过点 作 ,过点 作 , 与 相交于点 .
(1) 求证:四边形 是矩形.
(2) 若 ,,求四边形 的周长.
如图,已知平行四边形 中, 是它的一条对角线,过 , 两点作 ,,垂足分别为 ,,延长 , 分别交 , 于点 ,.
(1) 求证:四边形 是平行四边形.
(2) 已知 ,,求 的长.
已知在平行四边形 中,点 , 在对角线 上,,点 , 在 , 延长线上,,连接 ,.试判断线段 与 的关系,并说明理由.
如图,已知点 , 分别是平行四边形 的边 , 上的中点,且 .
(1) 求证:四边形 是菱形.
(2) 若 ,,求菱形 面积.
如图,在矩形 中,对角线 的垂直平分线 与 相交于点 ,与 相交于点 ,与 相交于点 ,连接 ,.
(1) 求证:四边形 是菱形;
(2) 若 ,,求 的长.
如图,将平行四边形 的边 延长到点 ,使 , 交边 于点 .
(1) 求证:;
(2) 若 ,求证:四边形 是矩形.
如图,四边形 中,,,点 为 中点,射线 平分 ,交 的延长线于点 ,连接 .
(1) 求证:四边形 是菱形.
(2) 若 ,,求 的长.
如图,菱形 的对角线 和 交于点 ,分别过点 , 作 ,, 和 交于点 .
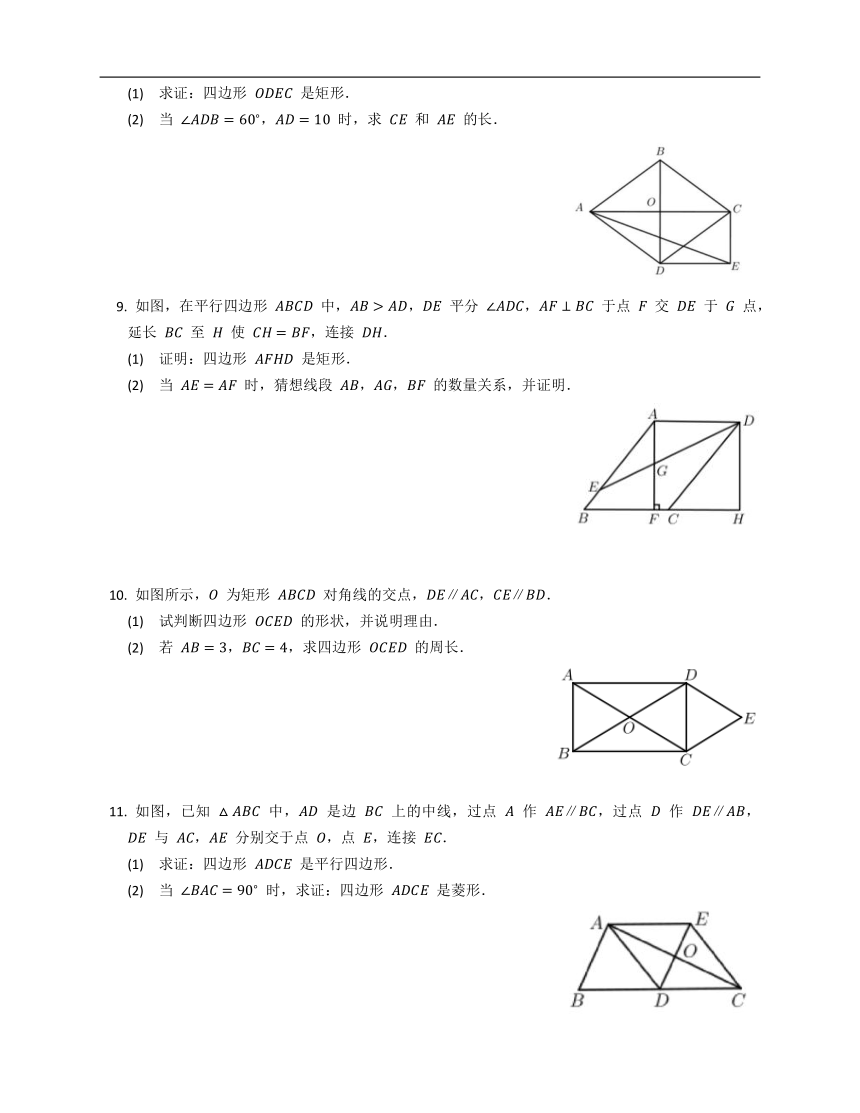
(1) 求证:四边形 是矩形.
(2) 当 , 时,求 和 的长.
如图,在平行四边形 中,, 平分 , 于点 交 于 点,延长 至 使 ,连接 .
(1) 证明:四边形 是矩形.
(2) 当 时,猜想线段 ,, 的数量关系,并证明.
如图所示, 为矩形 对角线的交点,,.
(1) 试判断四边形 的形状,并说明理由.
(2) 若 ,,求四边形 的周长.
如图,已知 中, 是边 上的中线,过点 作 ,过点 作 , 与 , 分别交于点 ,点 ,连接 .
(1) 求证:四边形 是平行四边形.
(2) 当 时,求证:四边形 是菱形.
在矩形 中, 于点 ,点 是边 上一点, 于点 ,.
(1) 试判断四边形 的形状,并说明理由.
(2) 若 ,,求四边形 的周长.
如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1) 求证:.
(2) 若 ,试判断四边形 的形状,并证明你的结论.
如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1) 试判断四边形 的形状,并证明;
(2) 若 试判断四边形 的形状,并证明.
已知:如图,四边形 的对角线 , 相交于点 ,,.
(1) 求证:四边形 是矩形;
(2) 如果点 在边 上, 平分 ,,求证:.
如图,在四边形 中,,,,点 为 的中点.
(1) 求证:四边形 是菱形;
(2) 连接 ,如果 平分 ,,求 的长.
已知:如图,在 中,,点 是斜边 的中点,,且 .
(1) 求证:;
(2) 求证:四边形 是菱形.
矩形 中 ,, 平分 交 于 , 平分 交 于 .
(1) 说明四边形 为平行四边形;
(2) 求四边形 的面积.
如图,在 中,, 是 边的中点,点 , 分别在 及其延长线上,且 ,连接 ,.
(1) 求证:四边形 是菱形;
(2) 若 ,,求四边形 的面积.
已知如图,在菱形 中,对角线 , 相交于点 ,,.
(1) 求证:四边形 是矩形.
(2) 若 ,,求四边形 的面积.
如图,已知菱形 中,对角线 相交于点 ,过点 作 ,过点 作 , 与 相交于点 .
(1) 求证:四边形 是矩形.
(2) 若 ,,求四边形 的周长.
如图,已知平行四边形 中, 是它的一条对角线,过 , 两点作 ,,垂足分别为 ,,延长 , 分别交 , 于点 ,.
(1) 求证:四边形 是平行四边形.
(2) 已知 ,,求 的长.
已知在平行四边形 中,点 , 在对角线 上,,点 , 在 , 延长线上,,连接 ,.试判断线段 与 的关系,并说明理由.
如图,已知点 , 分别是平行四边形 的边 , 上的中点,且 .
(1) 求证:四边形 是菱形.
(2) 若 ,,求菱形 面积.
如图,在矩形 中,对角线 的垂直平分线 与 相交于点 ,与 相交于点 ,与 相交于点 ,连接 ,.
(1) 求证:四边形 是菱形;
(2) 若 ,,求 的长.
如图,将平行四边形 的边 延长到点 ,使 , 交边 于点 .
(1) 求证:;
(2) 若 ,求证:四边形 是矩形.
如图,四边形 中,,,点 为 中点,射线 平分 ,交 的延长线于点 ,连接 .
(1) 求证:四边形 是菱形.
(2) 若 ,,求 的长.
如图,菱形 的对角线 和 交于点 ,分别过点 , 作 ,, 和 交于点 .
(1) 求证:四边形 是矩形.
(2) 当 , 时,求 和 的长.
如图,在平行四边形 中,, 平分 , 于点 交 于 点,延长 至 使 ,连接 .
(1) 证明:四边形 是矩形.
(2) 当 时,猜想线段 ,, 的数量关系,并证明.
如图所示, 为矩形 对角线的交点,,.
(1) 试判断四边形 的形状,并说明理由.
(2) 若 ,,求四边形 的周长.
如图,已知 中, 是边 上的中线,过点 作 ,过点 作 , 与 , 分别交于点 ,点 ,连接 .
(1) 求证:四边形 是平行四边形.
(2) 当 时,求证:四边形 是菱形.
在矩形 中, 于点 ,点 是边 上一点, 于点 ,.
(1) 试判断四边形 的形状,并说明理由.
(2) 若 ,,求四边形 的周长.
如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1) 求证:.
(2) 若 ,试判断四边形 的形状,并证明你的结论.
如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1) 试判断四边形 的形状,并证明;
(2) 若 试判断四边形 的形状,并证明.
已知:如图,四边形 的对角线 , 相交于点 ,,.
(1) 求证:四边形 是矩形;
(2) 如果点 在边 上, 平分 ,,求证:.
如图,在四边形 中,,,,点 为 的中点.
(1) 求证:四边形 是菱形;
(2) 连接 ,如果 平分 ,,求 的长.
已知:如图,在 中,,点 是斜边 的中点,,且 .
(1) 求证:;
(2) 求证:四边形 是菱形.
矩形 中 ,, 平分 交 于 , 平分 交 于 .
(1) 说明四边形 为平行四边形;
(2) 求四边形 的面积.
如图,在 中,, 是 边的中点,点 , 分别在 及其延长线上,且 ,连接 ,.
(1) 求证:四边形 是菱形;
(2) 若 ,,求四边形 的面积.
已知如图,在菱形 中,对角线 , 相交于点 ,,.
(1) 求证:四边形 是矩形.
(2) 若 ,,求四边形 的面积.
