第十八章 专题五 正方形的对角线与对角互补型-专题六 正方形与婆罗摩箥多变式图 热点专练(含答案)
文档属性
| 名称 | 第十八章 专题五 正方形的对角线与对角互补型-专题六 正方形与婆罗摩箥多变式图 热点专练(含答案) | 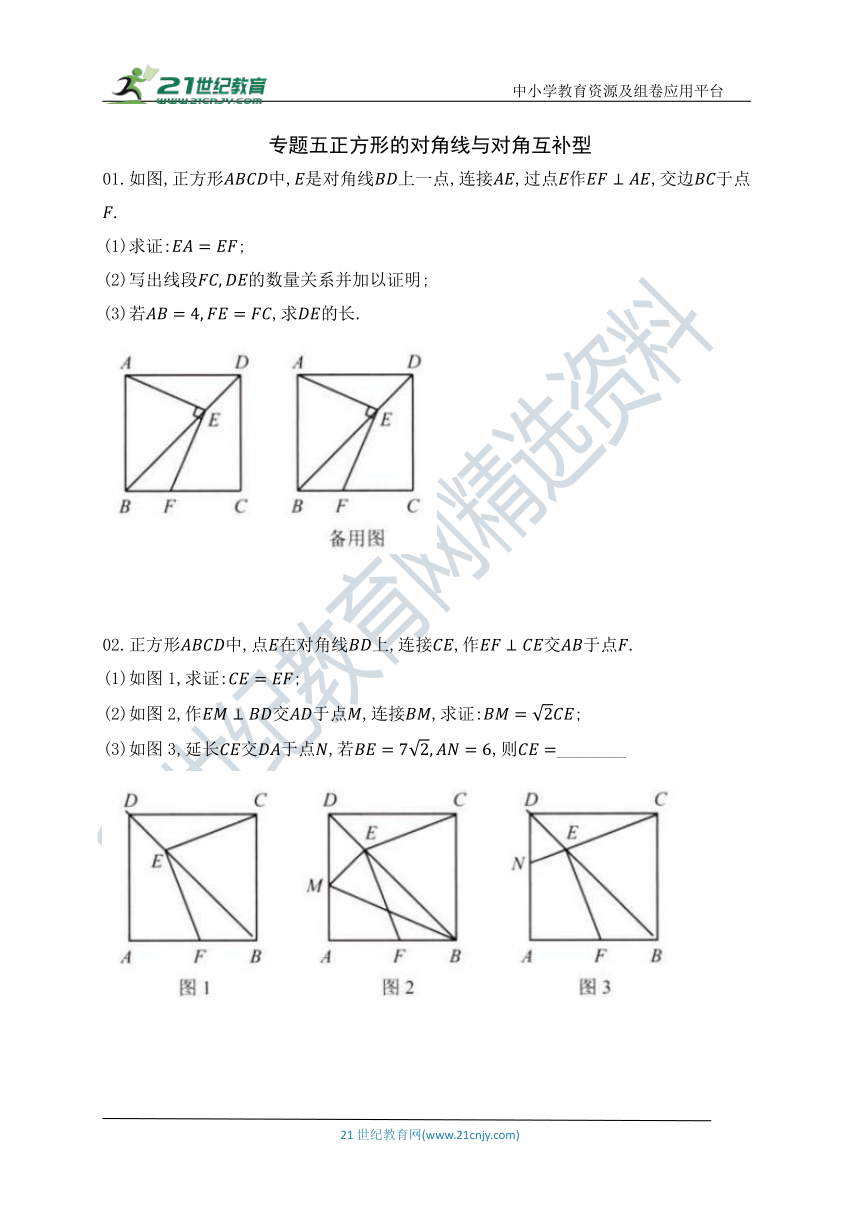 | |
| 格式 | docx | ||
| 文件大小 | 269.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 10:44:28 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题五正方形的对角线与对角互补型
01.如图,正方形中,是对角线上一点,连接,过点作,交边于点.
(1)求证:;
(2)写出线段的数量关系并加以证明;
(3)若,求的长.
02.正方形中,点在对角线上,连接,作交于点.
(1)如图1,求证:;
(2)如图2,作交于点,连接,求证:;
(3)如图3,延长交于点,若,则________
专题六正方形与婆罗摩箥多变式图
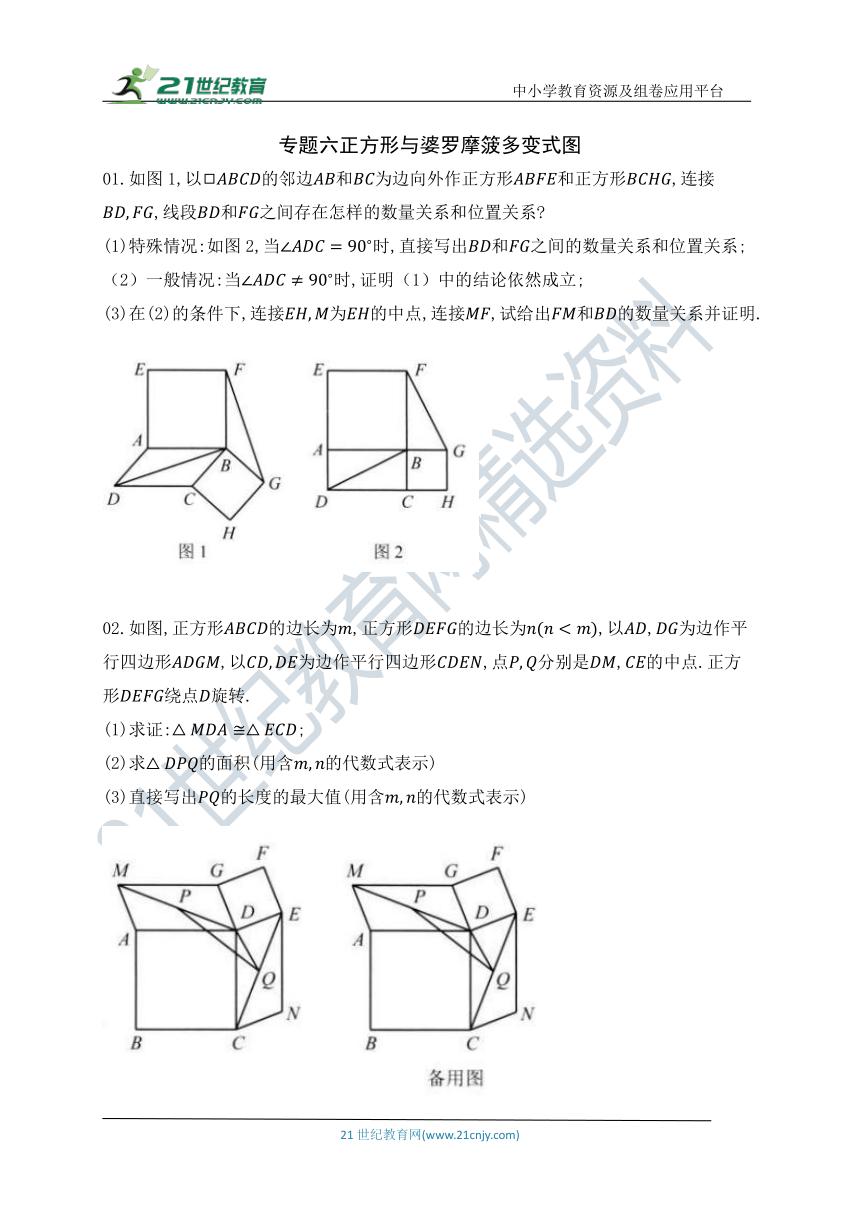
01.如图1,以的邻边和为边向外作正方形和正方形,连接,线段和之间存在怎样的数量关系和位置关系
(1)特殊情况:如图2,当时,直接写出和之间的数量关系和位置关系;
(2)一般情况:当时,证明(1)中的结论依然成立;
(3)在(2)的条件下,连接为的中点,连接,试给出和的数量关系并证明.
02.如图,正方形的边长为,正方形的边长为,以,为边作平行四边形,以为边作平行四边形,点分别是,的中点.正方形绕点旋转.
(1)求证:;
(2)求的面积(用含的代数式表示)
(3)直接写出的长度的最大值(用含的代数式表示)
专题五正方形的对角线与对角互补型
1.
(1)证明:过点作于,交于点,
四边形为正方形,,
四边形为矩形,,
,
.
.
(2)解:,理由如下:由(1)知,四边形为矩形,;
(3)解:连接,由正方形轴对称性得,由(1)得.
是等边三角形
设,则,
.
2.
(1)证明:连,则,
,
.
(2)证明:取中点,连,
导角可得.
等脮Rt.
图1图2
(3)解:过点作,分别交于点,
作于点,设
.
,
(舍去),
专题六正方形与婆罗摩笈多变式图
1.
解:(1)数量关系为:;位置关系为:.
(2)当时,(1)中的结论依然成立.
(3)延长至点,使得,连接,延长交于点,为的中点,.,.
.
.
.由(2)得:,设,
为的中点,
2.
,设,
,Rt中,,Rt中,,
两式相减得
(3)解:四边形是平行四边形,为中点,点在上.连接.
,
21世纪教育网(www.21cnjy.com)
专题五正方形的对角线与对角互补型
01.如图,正方形中,是对角线上一点,连接,过点作,交边于点.
(1)求证:;
(2)写出线段的数量关系并加以证明;
(3)若,求的长.
02.正方形中,点在对角线上,连接,作交于点.
(1)如图1,求证:;
(2)如图2,作交于点,连接,求证:;
(3)如图3,延长交于点,若,则________
专题六正方形与婆罗摩箥多变式图
01.如图1,以的邻边和为边向外作正方形和正方形,连接,线段和之间存在怎样的数量关系和位置关系
(1)特殊情况:如图2,当时,直接写出和之间的数量关系和位置关系;
(2)一般情况:当时,证明(1)中的结论依然成立;
(3)在(2)的条件下,连接为的中点,连接,试给出和的数量关系并证明.
02.如图,正方形的边长为,正方形的边长为,以,为边作平行四边形,以为边作平行四边形,点分别是,的中点.正方形绕点旋转.
(1)求证:;
(2)求的面积(用含的代数式表示)
(3)直接写出的长度的最大值(用含的代数式表示)
专题五正方形的对角线与对角互补型
1.
(1)证明:过点作于,交于点,
四边形为正方形,,
四边形为矩形,,
,
.
.
(2)解:,理由如下:由(1)知,四边形为矩形,;
(3)解:连接,由正方形轴对称性得,由(1)得.
是等边三角形
设,则,
.
2.
(1)证明:连,则,
,
.
(2)证明:取中点,连,
导角可得.
等脮Rt.
图1图2
(3)解:过点作,分别交于点,
作于点,设
.
,
(舍去),
专题六正方形与婆罗摩笈多变式图
1.
解:(1)数量关系为:;位置关系为:.
(2)当时,(1)中的结论依然成立.
(3)延长至点,使得,连接,延长交于点,为的中点,.,.
.
.
.由(2)得:,设,
为的中点,
2.
,设,
,Rt中,,Rt中,,
两式相减得
(3)解:四边形是平行四边形,为中点,点在上.连接.
,
21世纪教育网(www.21cnjy.com)
