18.2.1 矩形的性质同步测试题(含答案)
文档属性
| 名称 | 18.2.1 矩形的性质同步测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
矩形的性质同步测试
选择题.
1.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
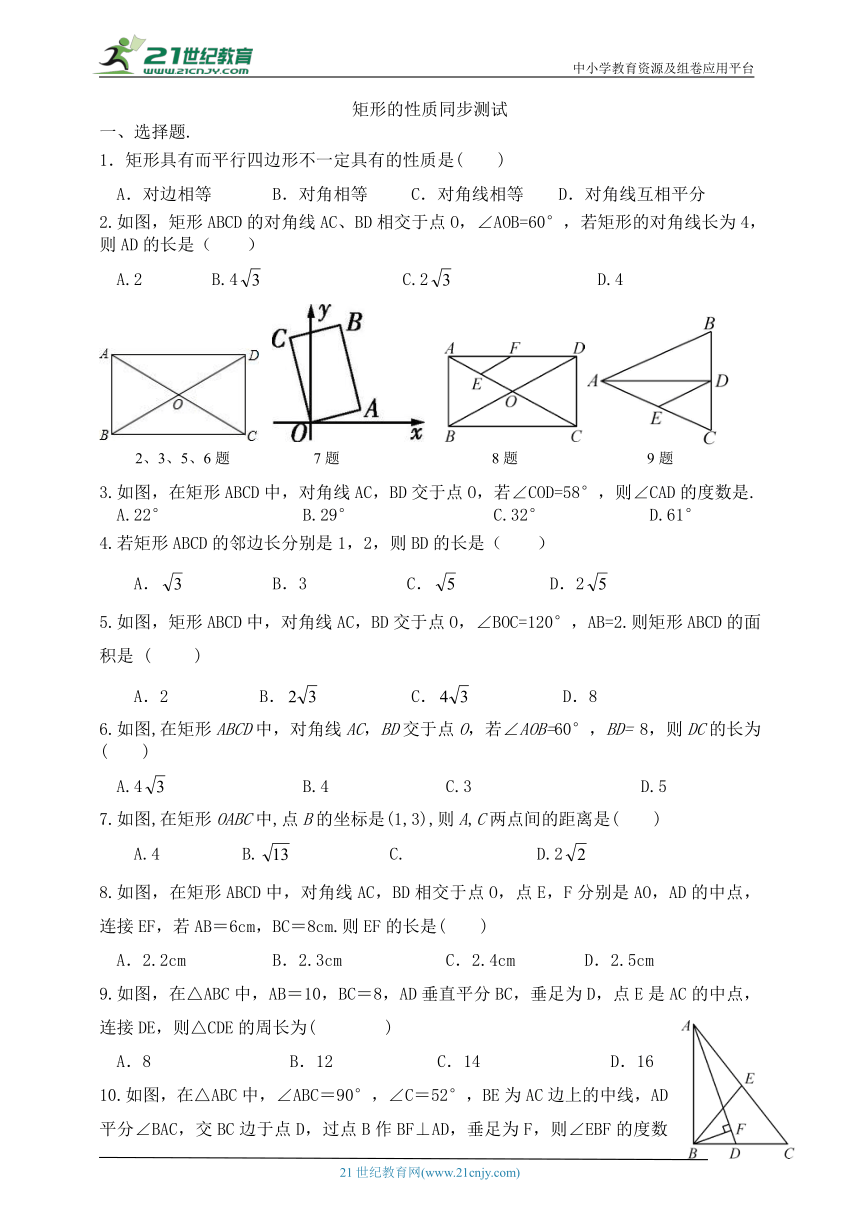
2.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=60°,若矩形的对角线长为4,则AD的长是( )
A.2 B.4 C.2 D.4
3.如图,在矩形ABCD中,对角线AC,BD交于点O,若∠COD=58°,则∠CAD的度数是.
A.22° B.29° C.32° D.61°
4.若矩形ABCD的邻边长分别是1,2,则BD的长是( )
A. B.3 C. D.2
5.如图,矩形ABCD中,对角线AC,BD交于点O,∠BOC=120°,AB=2.则矩形ABCD的面积是 ( )
A.2 B. C. D.8
6.如图,在矩形ABCD中,对角线AC,BD交于点O,若∠AOB=60°,BD= 8,则DC的长为( )
A.4 B.4 C.3 D.5
7.如图,在矩形OABC中,点B的坐标是(1,3),则A,C两点间的距离是( )
A.4 B. C. D.2
8.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是( )
A.2.2cm B.2.3cm C.2.4cm D.2.5cm
9.如图,在△ABC中,AB=10,BC=8,AD垂直平分BC,垂足为D,点E是AC的中点,连接DE,则△CDE的周长为( )
A.8 B.12 C.14 D.16
10.如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为
A.19° B.33° C.34° D.43°
填空题.
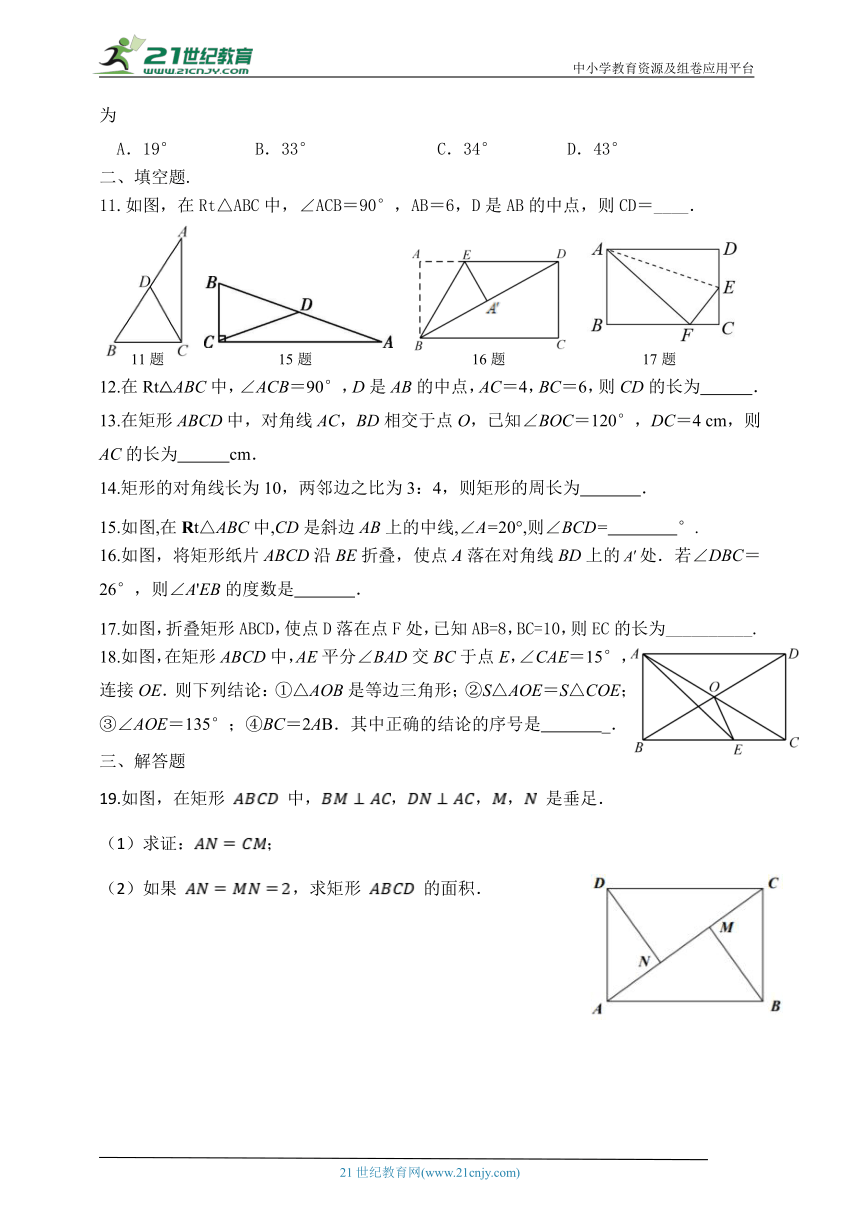
11.如图,在Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD=____.
12.在Rt△ABC中,∠ACB=90°,D是AB的中点,AC=4,BC=6,则CD的长为 .
13.在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=4 cm,则AC的长为 cm.
14.矩形的对角线长为10,两邻边之比为3:4,则矩形的周长为 .
15.如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20°,则∠BCD= °.
16.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的处.若∠DBC=26°,则∠A'EB的度数是 .
17.如图,折叠矩形ABCD,使点D落在点F处,已知AB=8,BC=10,则EC的长为__________.
18.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE.则下列结论:①△AOB是等边三角形;②S△AOE=S△COE;③∠AOE=135°;④BC=2AB.其中正确的结论的序号是 _.
三、解答题
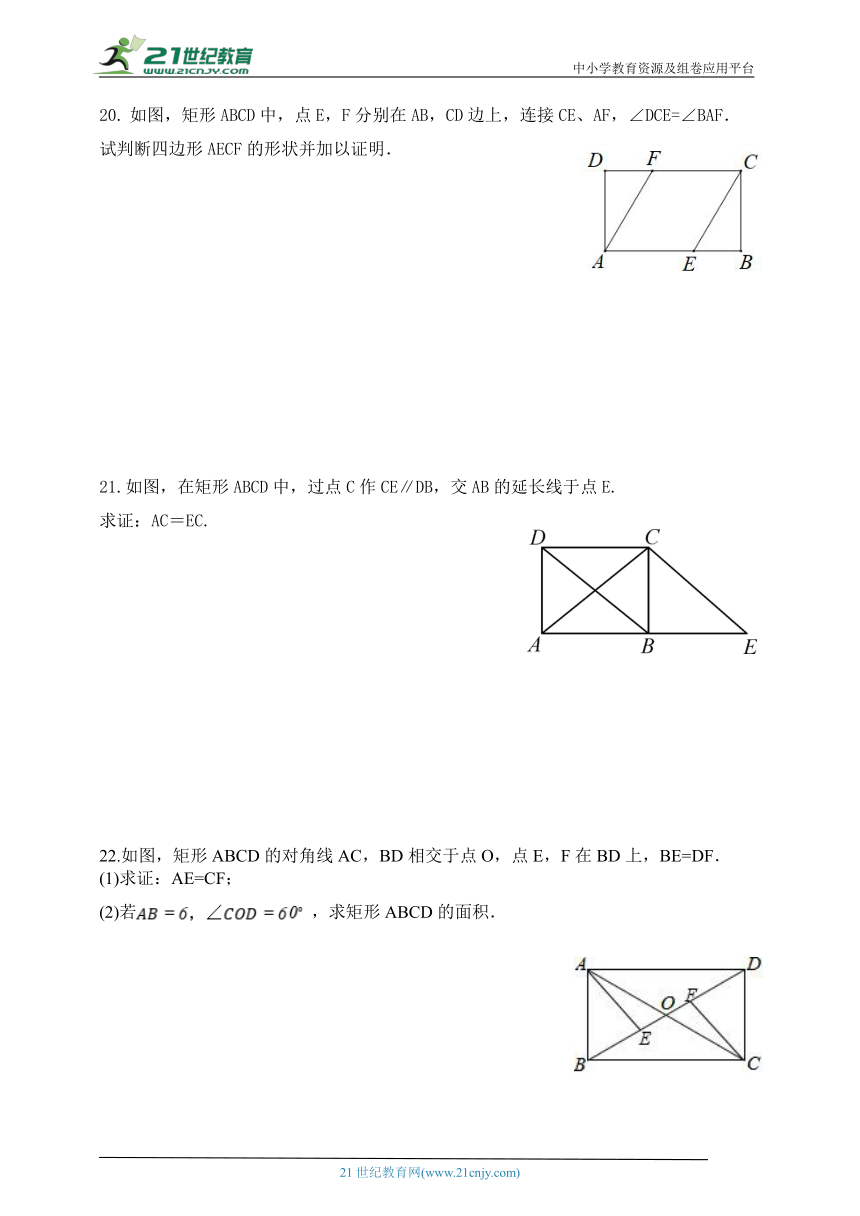
19.如图,在矩形 中,,,, 是垂足.
(1)求证:;
(2)如果 ,求矩形 的面积.
如图,矩形ABCD中,点E,F分别在AB,CD边上,连接CE、AF,∠DCE=∠BAF.
试判断四边形AECF的形状并加以证明.
21.如图,在矩形ABCD中,过点C作CE∥DB,交AB的延长线于点E.
求证:AC=EC.
22.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若 ,求矩形ABCD的面积.
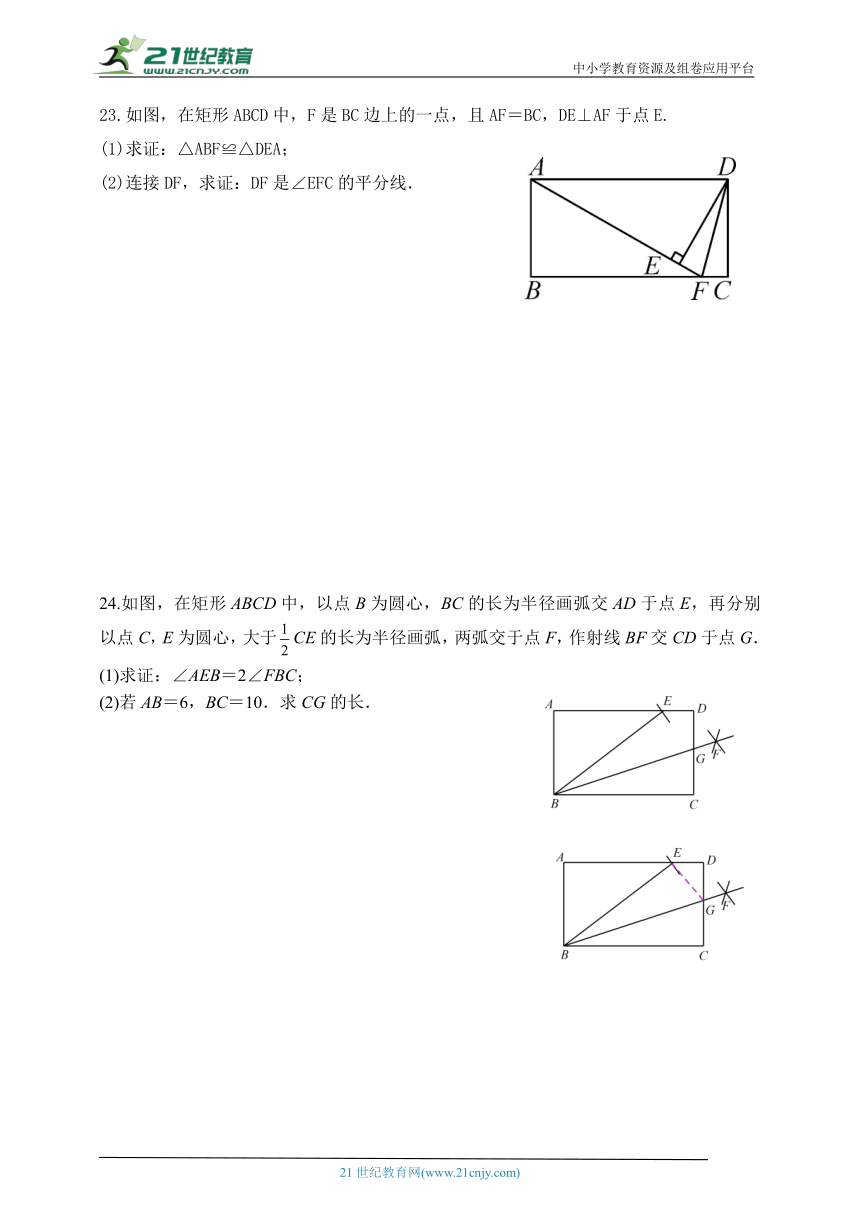
23.如图,在矩形ABCD中,F是BC边上的一点,且AF=BC,DE⊥AF于点E.
(1)求证:△ABF≌△DEA;
(2)连接DF,求证:DF是∠EFC的平分线.
24.如图,在矩形ABCD中,以点B为圆心,BC的长为半径画弧交AD于点E,再分别以点C,E为圆心,大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G.
(1)求证:∠AEB=2∠FBC;
(2)若AB=6,BC=10.求CG的长.
参考答案
选择题
1.C
2.C
3.B
4.C
5.C
6.B
7.C
8.D
9.C
10.B
二、填空题
11. 3
12.
13.8
14.28
15.70
16.58°
17.3
①②③
解答题
19题.
20题.
21题.
22题.
23题.
∴∠EFD=∠CFD
∴DF是∠EFC的平分线
24题.(1)证明:由作图可知:BF平分∠EBC
∴∠EBC=2∠FBC
∵矩形ABCD
∴AD∥BC
∴∠AEB=∠EBC
∴∠AEB=2∠FBC
(2)由作图可知:BC=BE=10
在Rt△ABE中,由勾股定理得:
AE=
∴DE=10-8=2
∵BC=BE,∠EBG=∠CBG,BG=BG
∴△EBG≌△∠CBG
∴EG=CG
设EG=CG=x,则DG=6-x.
在Rt△EDG中,由勾股定理得:
2 +(6-x) =x
解得:x=
∴CG的长为.
2、3、5、6题 7题 8题 9题
11题 15题 16题 17题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
矩形的性质同步测试
选择题.
1.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
2.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=60°,若矩形的对角线长为4,则AD的长是( )
A.2 B.4 C.2 D.4
3.如图,在矩形ABCD中,对角线AC,BD交于点O,若∠COD=58°,则∠CAD的度数是.
A.22° B.29° C.32° D.61°
4.若矩形ABCD的邻边长分别是1,2,则BD的长是( )
A. B.3 C. D.2
5.如图,矩形ABCD中,对角线AC,BD交于点O,∠BOC=120°,AB=2.则矩形ABCD的面积是 ( )
A.2 B. C. D.8
6.如图,在矩形ABCD中,对角线AC,BD交于点O,若∠AOB=60°,BD= 8,则DC的长为( )
A.4 B.4 C.3 D.5
7.如图,在矩形OABC中,点B的坐标是(1,3),则A,C两点间的距离是( )
A.4 B. C. D.2
8.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是( )
A.2.2cm B.2.3cm C.2.4cm D.2.5cm
9.如图,在△ABC中,AB=10,BC=8,AD垂直平分BC,垂足为D,点E是AC的中点,连接DE,则△CDE的周长为( )
A.8 B.12 C.14 D.16
10.如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为
A.19° B.33° C.34° D.43°
填空题.
11.如图,在Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD=____.
12.在Rt△ABC中,∠ACB=90°,D是AB的中点,AC=4,BC=6,则CD的长为 .
13.在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=4 cm,则AC的长为 cm.
14.矩形的对角线长为10,两邻边之比为3:4,则矩形的周长为 .
15.如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20°,则∠BCD= °.
16.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的处.若∠DBC=26°,则∠A'EB的度数是 .
17.如图,折叠矩形ABCD,使点D落在点F处,已知AB=8,BC=10,则EC的长为__________.
18.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE.则下列结论:①△AOB是等边三角形;②S△AOE=S△COE;③∠AOE=135°;④BC=2AB.其中正确的结论的序号是 _.
三、解答题
19.如图,在矩形 中,,,, 是垂足.
(1)求证:;
(2)如果 ,求矩形 的面积.
如图,矩形ABCD中,点E,F分别在AB,CD边上,连接CE、AF,∠DCE=∠BAF.
试判断四边形AECF的形状并加以证明.
21.如图,在矩形ABCD中,过点C作CE∥DB,交AB的延长线于点E.
求证:AC=EC.
22.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若 ,求矩形ABCD的面积.
23.如图,在矩形ABCD中,F是BC边上的一点,且AF=BC,DE⊥AF于点E.
(1)求证:△ABF≌△DEA;
(2)连接DF,求证:DF是∠EFC的平分线.
24.如图,在矩形ABCD中,以点B为圆心,BC的长为半径画弧交AD于点E,再分别以点C,E为圆心,大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G.
(1)求证:∠AEB=2∠FBC;
(2)若AB=6,BC=10.求CG的长.
参考答案
选择题
1.C
2.C
3.B
4.C
5.C
6.B
7.C
8.D
9.C
10.B
二、填空题
11. 3
12.
13.8
14.28
15.70
16.58°
17.3
①②③
解答题
19题.
20题.
21题.
22题.
23题.
∴∠EFD=∠CFD
∴DF是∠EFC的平分线
24题.(1)证明:由作图可知:BF平分∠EBC
∴∠EBC=2∠FBC
∵矩形ABCD
∴AD∥BC
∴∠AEB=∠EBC
∴∠AEB=2∠FBC
(2)由作图可知:BC=BE=10
在Rt△ABE中,由勾股定理得:
AE=
∴DE=10-8=2
∵BC=BE,∠EBG=∠CBG,BG=BG
∴△EBG≌△∠CBG
∴EG=CG
设EG=CG=x,则DG=6-x.
在Rt△EDG中,由勾股定理得:
2 +(6-x) =x
解得:x=
∴CG的长为.
2、3、5、6题 7题 8题 9题
11题 15题 16题 17题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
