完全平方公式(广东省深圳市福田区)

课件25张PPT。 1-8 完全平方公式
(1) 课堂小测验:
1). (-a-b)(a-b) 2 ). 199 × 201
3). 1999×2001 4 ). (x+y-3)(x-y+3)
5). (x+y-z)(x+y+z) 6). (2x-1)(4x2+1)(2x+1)
7 ).(2x2+3y3)(3y3-2x2) 8).
教学目的:
理解掌握完全平方公式特点, 会运用完全平方公式进行计算.
教学重点.难点:
重点和难点是完全平方公式的特点的理解及其运用完全平方公式进行计算.
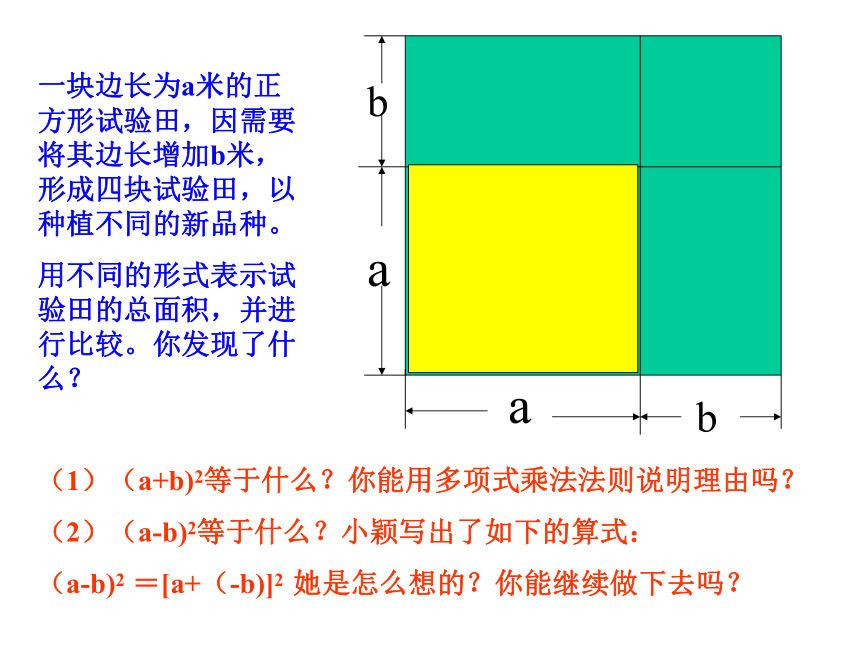
一块边长为a米的正方形试验田，因需要将其边长增加b米，形成四块试验田，以种植不同的新品种。
用不同的形式表示试验田的总面积，并进行比较。你发现了什么？（1）（a+b)2等于什么？你能用多项式乘法法则说明理由吗？
（2）（a-b)2等于什么？小颖写出了如下的算式：
（a-b)2 ＝[a+（-b)]2 她是怎么想的？你能继续做下去吗？完全平方公式
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2理解：1) 公式特点：
左边: 两数和的平方
右边: 首平方，尾平方，
2倍乘积在中间
2) a、b的广泛意义例1.计算:
(2) (2x-3y)2
(2) (-x+3y)2 (3) (-m-n)2读课本：p40--42
练习：p41 读一读
(a+b) 0 =1
(a+b)1=a+b
(a+b)2 = a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
例2.计算：
(1) (99)2
(2) (103)2
练习：计算：
（1） (67)2
（2） (1001)2
例4.已知a+b=7，ab=12，
求 a2+b2 , a2-ab+b2 , (a-b)2 的值
例5.已知 ，
求(1) (2)
例6.若x-2y=15，xy=-25，
求x2+4y2-1的值例7.已知 (a+b)2=4, (a-b)2=6,
求(1) a2+b2 (2) ab 的值
例8.已知a-b=2, ab=1, 求(a+b)2的值完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2理解：1) 公式结构：
左边: 两数和的平方
右边: 首平方，尾平方，
2倍乘积在中间
2) a、b的广泛意义课堂小结：注意：
特别是不要丢掉中间两倍乘积项布置作业:
课本: P43 1.13 1 . 2
轻松:P23-26 三个练习 p p19-23选择作1-8 完全平方公式
(2)教学目的:
是灵活运用完全平方公式进行计算.
教学重点.难点:
重点和难点是完全平方公式的掌握和灵活运用.
课堂小测验
1022 =
(1/2x-1)2 =
(-b2+3a2) 2=
(-x-y)2 =
(1/3ab-c)2 =
102041/4x2-x+1b4-6a2b2+9a4x2+2xy+y21/9a2b2-2/3abc+c2例1. 运用乘法公式计算
(1) (x+3)2-x2
(2) (a-b+3)(a+b-3)
(3) (a+b+c)2
(4) (a+b-c)2练习：p38 1、2练习二:计算
(1)
(2) (x+1)2(x-1)2(x2+1)2(x4+1)2
(a-2b+c)(a+2b-c)
(x+5)2-(x-2)(x-3)
(x+2y-z)2
练习一：p38 1、2例4. 运用乘法公式计算
(a+1)(a+3)(a+5)(a+7)
(3a2+1/2b)(3a2-1/2b)(9a2-1/4b)2
练习
(a+1)(a+2)(a+3)(a+4)
布置作业:
课本: P38 1.14 1. 2
P23-24拓展与迁移
(1) 若不论x取何值，多项式 x3-2x2- 4x-1
与 (x+1)(x2+mx+n)都相等, 求m.n (2) 求使 (x2+px+8)(x2-3x+q)的积中
不含 x2与x3项 p、q的值 (3) 求证：x(x+a) =(x+a/2)2-a2/4例5.计算例6.已知x2-y2=8，x+y=4，求x与y的值例7.化简(a+1)(a2+1)(a4+1)…(a2000+1) 例4.已知a+b=7，ab=12，求
a2+b2 , a2-ab+b2 , (a-b)2 的值
例5.已知 ，求
(1) (2)
例6.若x-2y=15，xy=-25，求
x2+4y2-1的值
例4. 运用乘法公式计算
(a+1)(a+3)(a+5)(a+7)例7.已知 (a+b)2=4, (a-b)2=6,
求(1) a2+b2 (2) ab 的值
例8.已知a-b=2, ab=1, 求(a+b)2的值例2.已知b2=ac，求证：
(a+b+c)(a-b+c)(a2-b2+c2)=a4+b4+c4例3已知:若(z-x)2-4(x-y)(y-z) =0
求证: X-2y+z=0