2023年人教版中考数学复习:圆(含答案)
文档属性
| 名称 | 2023年人教版中考数学复习:圆(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 815.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 18:18:41 | ||
图片预览

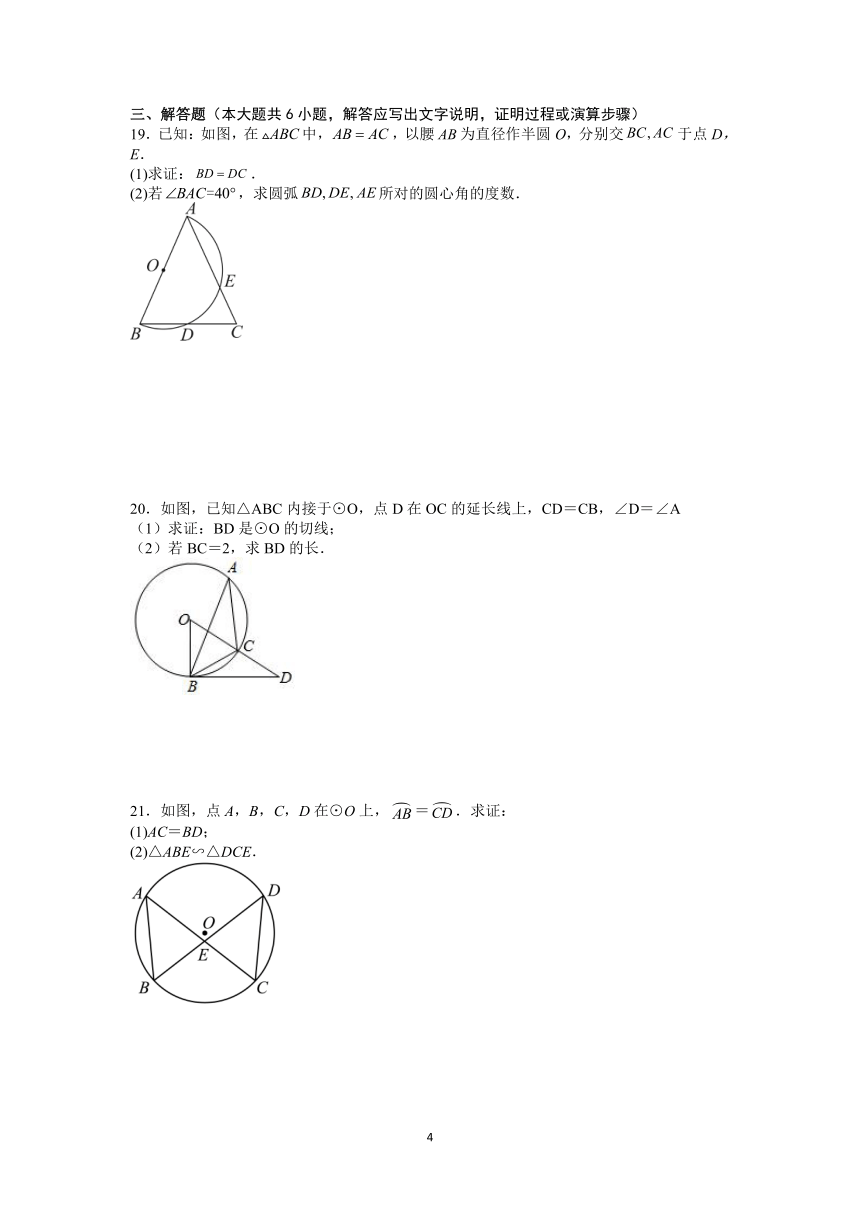
文档简介
2023年中考数学复习:圆
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共12小题,在每小题列出的选项中,选出符合题目的一项)
1.如图,在⊙O中,∠BOC=130°,点A在上,则∠BAC的度数为( )
A.55° B.65° C.75° D.130°
2.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A.6π B.2π C.π D.π
3.如图,在同一平面内,将边长相等的正六边形、正方形的一边重合,则∠1的度数为( )
A.18° B.25° C.30° D.45°
4.如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别是A,B,若∠APB=60°,PA=5,则弦AB的长是( )
A. B. C.5 D.5
5.如图,,,,,相互外离,它们的半径都是2,顺次连接五个圆心得到五边形,则图中五个扇形(阴影部分)的面积之和是( )
A. B. C. D.
6.如图,CD是⊙O的直径,弦AB⊥CD于点E,则下列结论不一定成立的是( )
A.AE=BE B.OE=DE C. D.
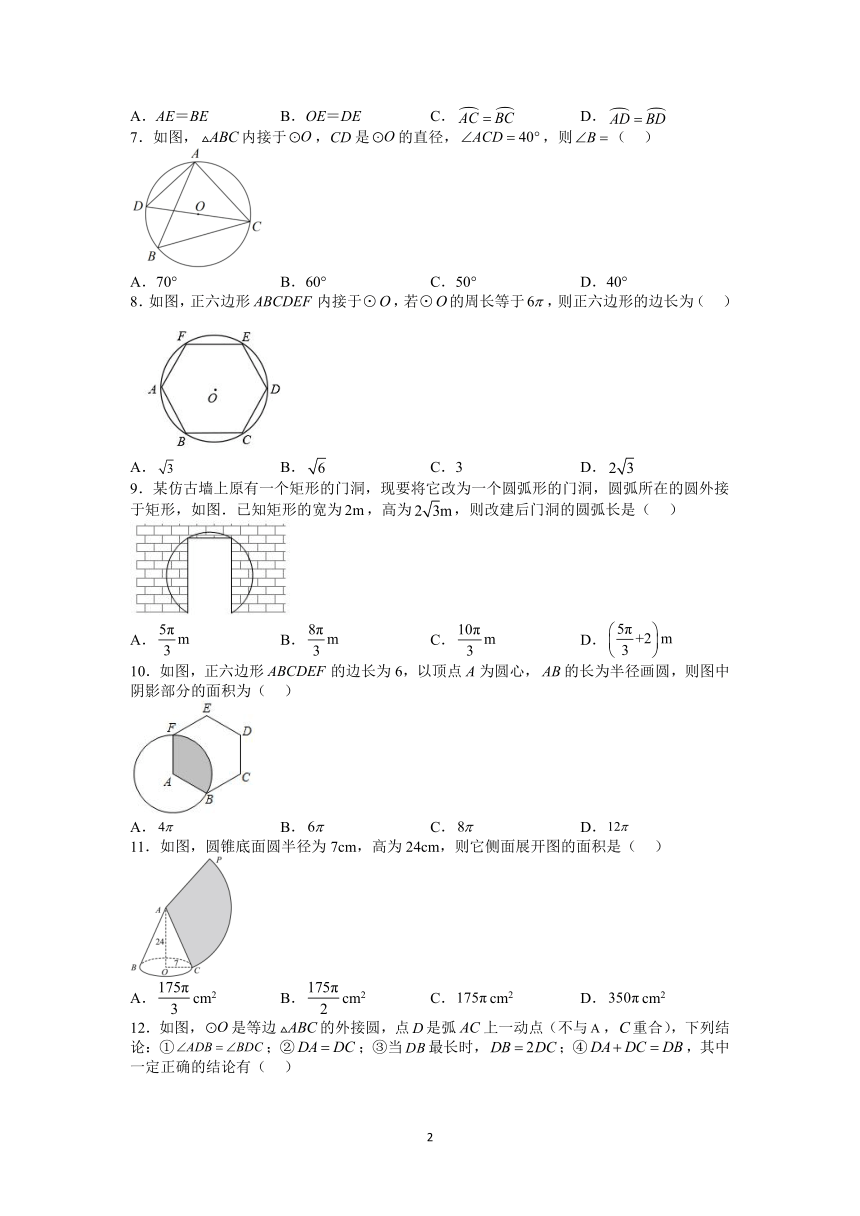
7.如图,内接于,CD是的直径,,则( )
A.70° B.60° C.50° D.40°
8.如图,正六边形内接于⊙,若⊙的周长等于,则正六边形的边长为( )
A. B. C.3 D.
9.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为,高为,则改建后门洞的圆弧长是( )
A. B. C. D.
10.如图,正六边形的边长为6,以顶点A为圆心,的长为半径画圆,则图中阴影部分的面积为( )
A. B. C. D.
11.如图,圆锥底面圆半径为7cm,高为24cm,则它侧面展开图的面积是( )
A.cm2 B.cm2 C.cm2 D.cm2
12.如图,是等边的外接圆,点是弧上一动点(不与,重合),下列结论:①;②;③当最长时,;④,其中一定正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,在横线上填上合理的答案)
13.扇形的半径为2,圆心角为90°,则该扇形的面积(结果保留)为____________.
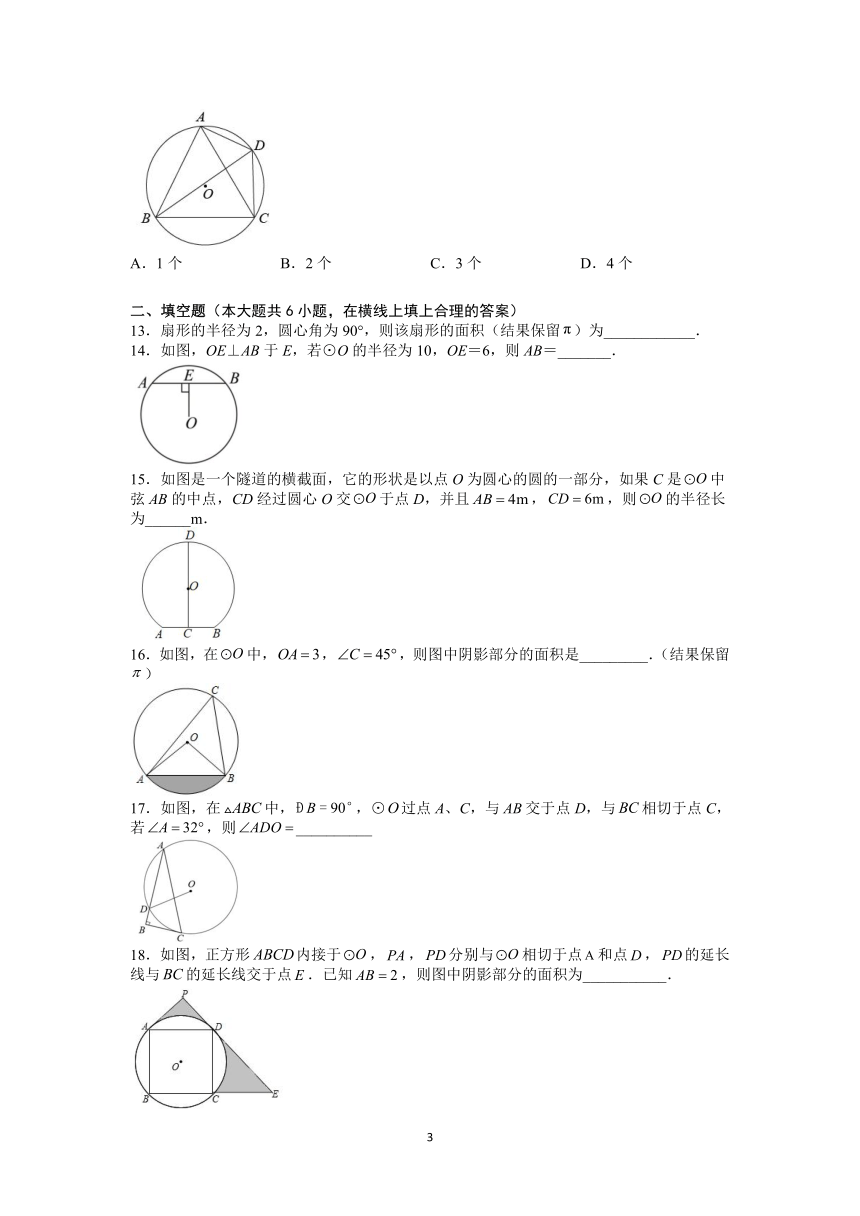
14.如图,OE⊥AB于E,若⊙O的半径为10,OE=6,则AB=_______.
15.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如果C是中弦AB的中点,CD经过圆心O交于点D,并且,,则的半径长为______m.
16.如图,在中,,,则图中阴影部分的面积是_________.(结果保留)
17.如图,在中,,⊙过点A、C,与交于点D,与相切于点C,若,则__________
18.如图,正方形内接于,,分别与相切于点和点,的延长线与的延长线交于点.已知,则图中阴影部分的面积为___________.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
19.已知:如图,在中,,以腰为直径作半圆O,分别交于点D,E.
(1)求证:.
(2)若,求圆弧所对的圆心角的度数.
20.如图,已知△ABC内接于⊙O,点D在OC的延长线上,CD=CB,∠D=∠A
(1)求证:BD是⊙O的切线;
(2)若BC=2,求BD的长.
21.如图,点A,B,C,D在⊙O上,=.求证:
(1)AC=BD;
(2)△ABE∽△DCE.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,过点D作DE⊥AC交AC于点E.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为5,BC=16,求DE的长.
23.如图,以线段为直径作,交射线于点,平分交于点,过点作直线于点,交的延长线于点.连接并延长交于点.
(1)求证:直线是的切线;
(2)求证:;
(3)若,,求的长.
24.如图,已知在Rt△ABC中,,D是AB边上一点,以BD为直径的半圆O与边AC相切,切点为E,过点O作,垂足为F.
(1)求证:;
(2)若,,求AD的长.
答案:
1.B
2.D
3.C
4.C
5.A
6.B
7.C
8.C
9.C
10.D
11.C
12.C
13.
14.16
15.
16.
17.
18.
19.(1)解:连接,
∵是圆的直径,
∴,
∴是的高,
∵,
∴.
(2)解:∵是圆的直径,
∴,
∴,
∵,
∴,
∴由圆周角定理得:所对的圆心角的度数是,
所对的圆心角的度数是,
所对的圆心角的度数是
20.(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
∴∠BOC+2∠OBC=180°,
∵∠BOC=2∠A,
∴∠A+∠OBC=90°,
又∵BC=CD,
∴∠D=∠CBD,
∵∠A=∠D,
∴∠CBD+∠OBC=90°,
∴∠OBD=90°,
∴OB⊥BD,
∴BD是⊙O的切线;
(2)解:∵∠OBD=90°,∠D=∠CBD,
∴∠OBC=∠BOC,
∴OC=BC,
又∵OB=OC,
∴△OBC为等边三角形,
∴∠BOC=60°,
∵BC=2,
∴OB=2,
∴BD=2.
21.(1)∵=
∴=
∴
∴BD=AC
(2)∵∠B=∠C
∠AEB=∠DEC
∴△ABE∽△DCE
22.(1)解:DE是⊙O的切线,理由如下:
连接OD,
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:连接AD,
∵∠ADB=90°,AB=AC,
∴BD=CD,
∵⊙O的半径为5,BC=16,
∴AC=AB=10,CD=8,
∴AD= ,
∵S△ADC=AC DE=AD CD,
∴DE=.
23.(1)证明:连接OD,则OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴ODAC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE是⊙O的切线.
(2)证明:线段是的直径,
,
∴∠ADM=180°-∠ADB=,
∴∠M+∠DAM=,∠ABM+∠DAB=,
∵∠DAM=∠DAB,
∴∠M=∠ABM,
∴AB=AM.
(3)解:∵∠AEF=90°,∠F=30°,
∴∠BAM=60°,
∴△ABM是等边三角形,
∴∠M=60°,
∵∠DEM=90°,ME=1,
∴∠EDM=30°,
∴MD=2ME=2,
∴BD=MD=2,
∵∠BDF=∠EDM=30°,
∴∠BDF=∠F,
∴BF=BD=2.
24.(1)解:如图,连接OE,
∵AC切半圆O于点E,
∴OE⊥AC,
∵OF⊥BC,,
∴∠OEC=∠OFC=∠C=90°.
∴四边形OFCE是矩形,
∴OF=EC;
(2)∵,
∴,
∵,OE⊥AC,
∴,
∴.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共12小题,在每小题列出的选项中,选出符合题目的一项)
1.如图,在⊙O中,∠BOC=130°,点A在上,则∠BAC的度数为( )
A.55° B.65° C.75° D.130°
2.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A.6π B.2π C.π D.π
3.如图,在同一平面内,将边长相等的正六边形、正方形的一边重合,则∠1的度数为( )
A.18° B.25° C.30° D.45°
4.如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别是A,B,若∠APB=60°,PA=5,则弦AB的长是( )
A. B. C.5 D.5
5.如图,,,,,相互外离,它们的半径都是2,顺次连接五个圆心得到五边形,则图中五个扇形(阴影部分)的面积之和是( )
A. B. C. D.
6.如图,CD是⊙O的直径,弦AB⊥CD于点E,则下列结论不一定成立的是( )
A.AE=BE B.OE=DE C. D.
7.如图,内接于,CD是的直径,,则( )
A.70° B.60° C.50° D.40°
8.如图,正六边形内接于⊙,若⊙的周长等于,则正六边形的边长为( )
A. B. C.3 D.
9.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为,高为,则改建后门洞的圆弧长是( )
A. B. C. D.
10.如图,正六边形的边长为6,以顶点A为圆心,的长为半径画圆,则图中阴影部分的面积为( )
A. B. C. D.
11.如图,圆锥底面圆半径为7cm,高为24cm,则它侧面展开图的面积是( )
A.cm2 B.cm2 C.cm2 D.cm2
12.如图,是等边的外接圆,点是弧上一动点(不与,重合),下列结论:①;②;③当最长时,;④,其中一定正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,在横线上填上合理的答案)
13.扇形的半径为2,圆心角为90°,则该扇形的面积(结果保留)为____________.
14.如图,OE⊥AB于E,若⊙O的半径为10,OE=6,则AB=_______.
15.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如果C是中弦AB的中点,CD经过圆心O交于点D,并且,,则的半径长为______m.
16.如图,在中,,,则图中阴影部分的面积是_________.(结果保留)
17.如图,在中,,⊙过点A、C,与交于点D,与相切于点C,若,则__________
18.如图,正方形内接于,,分别与相切于点和点,的延长线与的延长线交于点.已知,则图中阴影部分的面积为___________.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
19.已知:如图,在中,,以腰为直径作半圆O,分别交于点D,E.
(1)求证:.
(2)若,求圆弧所对的圆心角的度数.
20.如图,已知△ABC内接于⊙O,点D在OC的延长线上,CD=CB,∠D=∠A
(1)求证:BD是⊙O的切线;
(2)若BC=2,求BD的长.
21.如图,点A,B,C,D在⊙O上,=.求证:
(1)AC=BD;
(2)△ABE∽△DCE.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,过点D作DE⊥AC交AC于点E.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为5,BC=16,求DE的长.
23.如图,以线段为直径作,交射线于点,平分交于点,过点作直线于点,交的延长线于点.连接并延长交于点.
(1)求证:直线是的切线;
(2)求证:;
(3)若,,求的长.
24.如图,已知在Rt△ABC中,,D是AB边上一点,以BD为直径的半圆O与边AC相切,切点为E,过点O作,垂足为F.
(1)求证:;
(2)若,,求AD的长.
答案:
1.B
2.D
3.C
4.C
5.A
6.B
7.C
8.C
9.C
10.D
11.C
12.C
13.
14.16
15.
16.
17.
18.
19.(1)解:连接,
∵是圆的直径,
∴,
∴是的高,
∵,
∴.
(2)解:∵是圆的直径,
∴,
∴,
∵,
∴,
∴由圆周角定理得:所对的圆心角的度数是,
所对的圆心角的度数是,
所对的圆心角的度数是
20.(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
∴∠BOC+2∠OBC=180°,
∵∠BOC=2∠A,
∴∠A+∠OBC=90°,
又∵BC=CD,
∴∠D=∠CBD,
∵∠A=∠D,
∴∠CBD+∠OBC=90°,
∴∠OBD=90°,
∴OB⊥BD,
∴BD是⊙O的切线;
(2)解:∵∠OBD=90°,∠D=∠CBD,
∴∠OBC=∠BOC,
∴OC=BC,
又∵OB=OC,
∴△OBC为等边三角形,
∴∠BOC=60°,
∵BC=2,
∴OB=2,
∴BD=2.
21.(1)∵=
∴=
∴
∴BD=AC
(2)∵∠B=∠C
∠AEB=∠DEC
∴△ABE∽△DCE
22.(1)解:DE是⊙O的切线,理由如下:
连接OD,
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:连接AD,
∵∠ADB=90°,AB=AC,
∴BD=CD,
∵⊙O的半径为5,BC=16,
∴AC=AB=10,CD=8,
∴AD= ,
∵S△ADC=AC DE=AD CD,
∴DE=.
23.(1)证明:连接OD,则OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴ODAC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE是⊙O的切线.
(2)证明:线段是的直径,
,
∴∠ADM=180°-∠ADB=,
∴∠M+∠DAM=,∠ABM+∠DAB=,
∵∠DAM=∠DAB,
∴∠M=∠ABM,
∴AB=AM.
(3)解:∵∠AEF=90°,∠F=30°,
∴∠BAM=60°,
∴△ABM是等边三角形,
∴∠M=60°,
∵∠DEM=90°,ME=1,
∴∠EDM=30°,
∴MD=2ME=2,
∴BD=MD=2,
∵∠BDF=∠EDM=30°,
∴∠BDF=∠F,
∴BF=BD=2.
24.(1)解:如图,连接OE,
∵AC切半圆O于点E,
∴OE⊥AC,
∵OF⊥BC,,
∴∠OEC=∠OFC=∠C=90°.
∴四边形OFCE是矩形,
∴OF=EC;
(2)∵,
∴,
∵,OE⊥AC,
∴,
∴.
同课章节目录
