2023年中考数学复习:平行四边形练习 (含答案)
文档属性
| 名称 | 2023年中考数学复习:平行四边形练习 (含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 591.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 00:00:00 | ||
图片预览



文档简介
2023年中考数学复行四边形
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共12小题,在每小题列出的选项中,选出符合题目的一项)
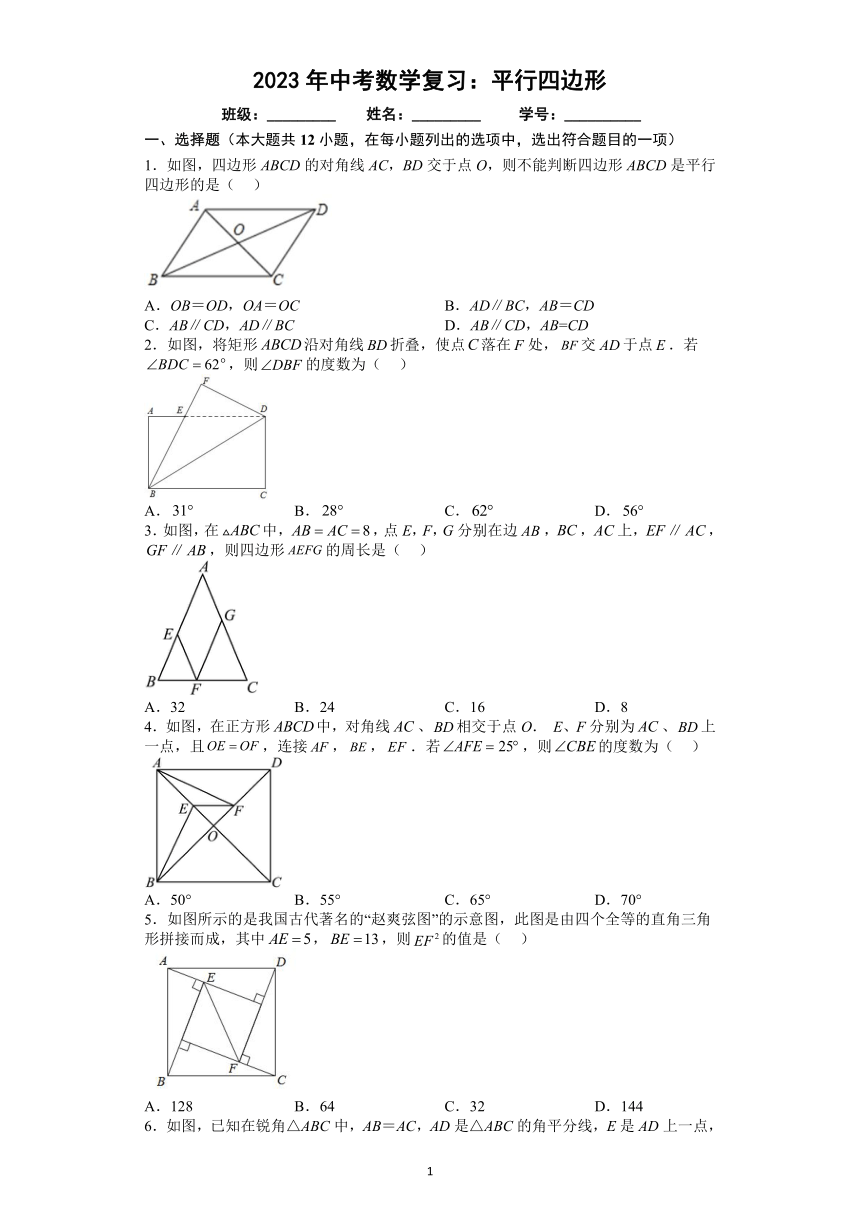
1.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.OB=OD,OA=OC B.AD∥BC,AB=CD
C.AB∥CD,AD∥BC D.AB∥CD,AB=CD
2.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
3.如图,在中,,点E,F,G分别在边,,上,,,则四边形的周长是( )
A.32 B.24 C.16 D.8
4.如图,在正方形中,对角线、相交于点O. E、F分别为、上一点,且,连接,,.若,则的度数为( )
A.50° B.55° C.65° D.70°
5.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中,,则的值是( )
A.128 B.64 C.32 D.144
6.如图,已知在锐角△ABC中,AB=AC,AD是△ABC的角平分线,E是AD上一点,连结EB,EC.若∠EBC=45°,BC=6,则△EBC的面积是( )
A.12 B.9 C.6 D.
7.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A. B. C.4 D.
8.如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )
A.35° B.40° C.45° D.50°
9.如图,在四边形ABCD中,,且AD=DC,则下列说法:①四边形ABCD是平行四边形;②AB=BC;③AC⊥BD;④AC平分∠BAD;⑤若AC=6,BD=8,则四边形ABCD的面积为24,其中正确的有( )
A.2个 B.3个 C.4个 D.5个
10.如图,P是面积为S的内任意一点,的面积为,的面积为,则( )
A. B.
C. D.的大小与P点位置有关
11.如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设,则 为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
12.如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A.当时,四边形ABMP为矩形
B.当时,四边形CDPM为平行四边形
C.当时,
D.当时,或6s
二、填空题(本大题共6小题,在横线上填上合理的答案)
13.如图,在Rt中,为斜边上的中线,若,则________.
14.如图,矩形的对角线,相交于点,//,//.若,则四边形的周长是_______.
15.如图,矩形中,,是的中点,线段在边上左右滑动;若,则的最小值为____________.
16.如图,△ABC的边BC长为4cm.将△ABC平移2cm得到△A′B′C′,且BB′⊥BC,则阴影部分的面积为______.
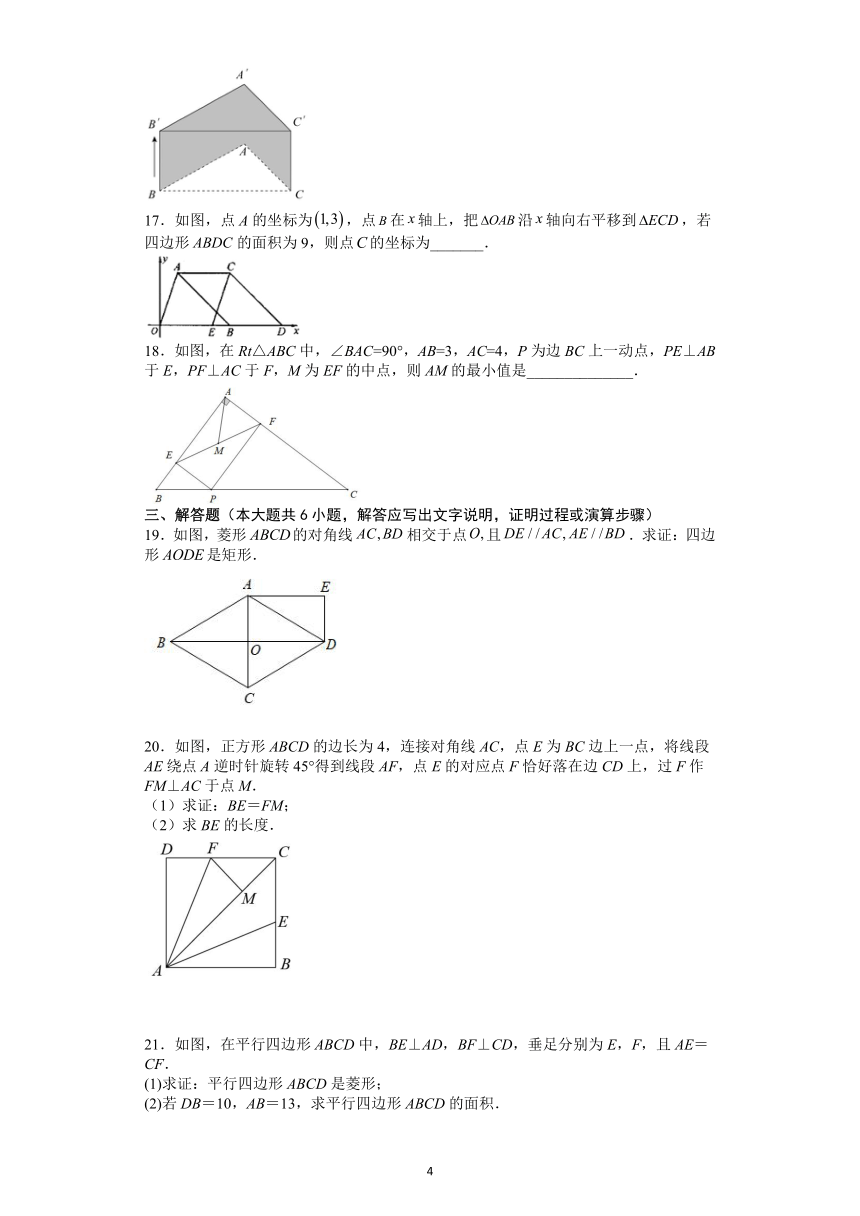
17.如图,点A的坐标为,点在轴上,把沿轴向右平移到,若四边形的面积为9,则点的坐标为_______.
18.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是______________.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
19.如图,菱形的对角线相交于点且.求证:四边形是矩形.
20.如图,正方形ABCD的边长为4,连接对角线AC,点E为BC边上一点,将线段AE绕点A逆时针旋转45°得到线段AF,点E的对应点F恰好落在边CD上,过F作FM⊥AC于点M.
(1)求证:BE=FM;
(2)求BE的长度.
21.如图,在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足分别为E,F,且AE=CF.
(1)求证:平行四边形ABCD是菱形;
(2)若DB=10,AB=13,求平行四边形ABCD的面积.
22.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,连接PE,PB.
(1)在AC上找一点P,使△BPE的周长最小(作图说明);
(2)求出△BPE周长的最小值.
23.如图,在四边形中,,;,,垂足分别为,.
(1)求证:≌;
(2)若与交于点,求证:.
24.如图,在四边形中,AB//DC,,对角线,交于点,平分,过点作交的延长线于点,连接.
(1)求证:四边形是菱形;
(2)若,,求的长.
试卷第1页,共3页
参考答案:
1.B 2.B 3.C 4.C 5.A 6.B 7.D 8.D 9.D 10.C 11.B 12.D
13.4 14.20 15. 16.8 17.(4,3) 18.
19.证明:四边形为菱形
四边形为平行四边形,
平行四边形是矩形.
20.(1)证明:在正方形ABCD中,线段AE绕点A逆时针旋转45°得到线段AF
∠CAB=45°,∠EAF=45°,AE=AF
∠FAM=∠EAB
∵FM⊥AC
∠FMA=∠B=90°
≌(AAS)
BE=FM
(2)在正方形ABCD中,边长为4
AC=,∠DCA=45°
≌
∴AM=AB=4
MC=AC—AM=—4
∵是等腰直角三角形
BE=MF=MC=—4
21.(1)证明:∵四边形ABCD是平行四边形,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∴平行四边形ABCD是菱形;
(2)
解: 如图所示:连接AC,交BD于点H,
∵四边形ABCD是菱形,
∴,
∵,,
∴,
在中,
,
∴,
∴平行四边形ABCD的面积为:.
22.(1)解:如图,连接DE,交AC于点P′,连接BP′,当点P在点P′处时,△BPE的周长最小.
理由:在正方形ABCD中,AB=AD,∠BAC=∠DAC,
∵AP′=AP′,
∴△ABP′≌△ADP′,
∴BP′=DP′,
∴BP+PE= DP′+ P′E≥DE,
即当点P位于PP′时,△BPE的周长PB+EP+BE最小;
(2)
解:由(1)得:B P′=DP′,
∴P′B+P′E=DE.
∵BE=2,AE=3BE,
∴AE=6.
∴AD=AB=8.
∴DE==10.
∴PB+PE的最小值是10.
∴△BPE周长的最小值为10+BE=10+2=12.
23.(1)证明:∵,,
∴,
∵,,
∴≌.
(2)由(1)≌,
∴,
∵,,
∴,
∵,
∴
∴.
24.(1)证明:∵AB//CD,
∴,
∵平分,
∴,
∴,
∴,
又∵,
∴,
又∵∥,
∴四边形是平行四边形,
又∵,
∴是菱形.
(2)解:∵四边形是菱形,对角线、交于点,
∴,,,
∴,
在Rt△AOB中,,
∴,
∵,
∴,
在Rt△AEC中,,为中点,
∴.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共12小题,在每小题列出的选项中,选出符合题目的一项)
1.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.OB=OD,OA=OC B.AD∥BC,AB=CD
C.AB∥CD,AD∥BC D.AB∥CD,AB=CD
2.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
3.如图,在中,,点E,F,G分别在边,,上,,,则四边形的周长是( )
A.32 B.24 C.16 D.8
4.如图,在正方形中,对角线、相交于点O. E、F分别为、上一点,且,连接,,.若,则的度数为( )
A.50° B.55° C.65° D.70°
5.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中,,则的值是( )
A.128 B.64 C.32 D.144
6.如图,已知在锐角△ABC中,AB=AC,AD是△ABC的角平分线,E是AD上一点,连结EB,EC.若∠EBC=45°,BC=6,则△EBC的面积是( )
A.12 B.9 C.6 D.
7.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A. B. C.4 D.
8.如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )
A.35° B.40° C.45° D.50°
9.如图,在四边形ABCD中,,且AD=DC,则下列说法:①四边形ABCD是平行四边形;②AB=BC;③AC⊥BD;④AC平分∠BAD;⑤若AC=6,BD=8,则四边形ABCD的面积为24,其中正确的有( )
A.2个 B.3个 C.4个 D.5个
10.如图,P是面积为S的内任意一点,的面积为,的面积为,则( )
A. B.
C. D.的大小与P点位置有关
11.如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设,则 为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
12.如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A.当时,四边形ABMP为矩形
B.当时,四边形CDPM为平行四边形
C.当时,
D.当时,或6s
二、填空题(本大题共6小题,在横线上填上合理的答案)
13.如图,在Rt中,为斜边上的中线,若,则________.
14.如图,矩形的对角线,相交于点,//,//.若,则四边形的周长是_______.
15.如图,矩形中,,是的中点,线段在边上左右滑动;若,则的最小值为____________.
16.如图,△ABC的边BC长为4cm.将△ABC平移2cm得到△A′B′C′,且BB′⊥BC,则阴影部分的面积为______.
17.如图,点A的坐标为,点在轴上,把沿轴向右平移到,若四边形的面积为9,则点的坐标为_______.
18.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是______________.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
19.如图,菱形的对角线相交于点且.求证:四边形是矩形.
20.如图,正方形ABCD的边长为4,连接对角线AC,点E为BC边上一点,将线段AE绕点A逆时针旋转45°得到线段AF,点E的对应点F恰好落在边CD上,过F作FM⊥AC于点M.
(1)求证:BE=FM;
(2)求BE的长度.
21.如图,在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足分别为E,F,且AE=CF.
(1)求证:平行四边形ABCD是菱形;
(2)若DB=10,AB=13,求平行四边形ABCD的面积.
22.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,连接PE,PB.
(1)在AC上找一点P,使△BPE的周长最小(作图说明);
(2)求出△BPE周长的最小值.
23.如图,在四边形中,,;,,垂足分别为,.
(1)求证:≌;
(2)若与交于点,求证:.
24.如图,在四边形中,AB//DC,,对角线,交于点,平分,过点作交的延长线于点,连接.
(1)求证:四边形是菱形;
(2)若,,求的长.
试卷第1页,共3页
参考答案:
1.B 2.B 3.C 4.C 5.A 6.B 7.D 8.D 9.D 10.C 11.B 12.D
13.4 14.20 15. 16.8 17.(4,3) 18.
19.证明:四边形为菱形
四边形为平行四边形,
平行四边形是矩形.
20.(1)证明:在正方形ABCD中,线段AE绕点A逆时针旋转45°得到线段AF
∠CAB=45°,∠EAF=45°,AE=AF
∠FAM=∠EAB
∵FM⊥AC
∠FMA=∠B=90°
≌(AAS)
BE=FM
(2)在正方形ABCD中,边长为4
AC=,∠DCA=45°
≌
∴AM=AB=4
MC=AC—AM=—4
∵是等腰直角三角形
BE=MF=MC=—4
21.(1)证明:∵四边形ABCD是平行四边形,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∴平行四边形ABCD是菱形;
(2)
解: 如图所示:连接AC,交BD于点H,
∵四边形ABCD是菱形,
∴,
∵,,
∴,
在中,
,
∴,
∴平行四边形ABCD的面积为:.
22.(1)解:如图,连接DE,交AC于点P′,连接BP′,当点P在点P′处时,△BPE的周长最小.
理由:在正方形ABCD中,AB=AD,∠BAC=∠DAC,
∵AP′=AP′,
∴△ABP′≌△ADP′,
∴BP′=DP′,
∴BP+PE= DP′+ P′E≥DE,
即当点P位于PP′时,△BPE的周长PB+EP+BE最小;
(2)
解:由(1)得:B P′=DP′,
∴P′B+P′E=DE.
∵BE=2,AE=3BE,
∴AE=6.
∴AD=AB=8.
∴DE==10.
∴PB+PE的最小值是10.
∴△BPE周长的最小值为10+BE=10+2=12.
23.(1)证明:∵,,
∴,
∵,,
∴≌.
(2)由(1)≌,
∴,
∵,,
∴,
∵,
∴
∴.
24.(1)证明:∵AB//CD,
∴,
∵平分,
∴,
∴,
∴,
又∵,
∴,
又∵∥,
∴四边形是平行四边形,
又∵,
∴是菱形.
(2)解:∵四边形是菱形,对角线、交于点,
∴,,,
∴,
在Rt△AOB中,,
∴,
∵,
∴,
在Rt△AEC中,,为中点,
∴.
同课章节目录
