§1.2 30°,45°,60°角的三角函数值[下学期]
文档属性
| 名称 | §1.2 30°,45°,60°角的三角函数值[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 32.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-10 18:51:00 | ||
图片预览

文档简介
第三课时 §1.2 30°,45°,60°角的三角函数值
教学目标
知识与能力目标
能够进行有关的推理.进一步体会三角函数的意义.会进行30°、45°、60°角的三角函数值的计算.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.
过程与方法目标
通过自主探索经历探索30°、45°、60°角的三角函数值的过程,发展学生观察、分析、发现的能力.培养学生把实际问题转化为数学问题的能力.
情感与价值观要求
通过数学活动,产生好奇心.培养学生独立思考问题的习惯,锻炼克服困难的意志,建立学好数学自信心.
教学重点
探索30°、45°、60°角的三角函数值; 含30°、45°、60°角的三角函数值的计算;锐角三角函数值的大小比较.
教学难点
进一步体会三角函数的意义.
教学过程
创设问题情境,引入新课
[问题]为了测量一棵大树的高度,准备了如下测量工具:①含30°和60°两个锐角的三角尺;②皮尺.请你设计一个测量方案,能测出一棵大树的高度.
让一位同学拿着三角尺站在一个适当的位置B处,使这位同学拿起三角尺,她的视线恰好和斜边重合且过树梢C点,30°的邻边和水平方向平行,用卷尺测出AB的长度,BE的长度,因为DE=AB,所以只需在Rt△CDA中求出CD的长度即可.
提示:在Rt△ACD中,∠CAD=30°,AD=BE,BE是已知的,设BE=a米,则AD=a米,如何求CD呢 含30°角的直角三角形有一个非常重要的性质:30°的角所对的边等于斜边的一半,即AC=2CD,根据勾股定理,(2CD)2=CD2+a2.CD=a.则树的高度即可求出.
[师]我们前面学习了三角函数的定义,如果一个角的大小确定,那么它的正切、正弦、余弦值也随之确定,如果能求出30°的正切值,在上图中,tan30°=,则CD=atan30°,岂不简单.你能求出30°角的三个三角函数值吗
师生互动、学习新课
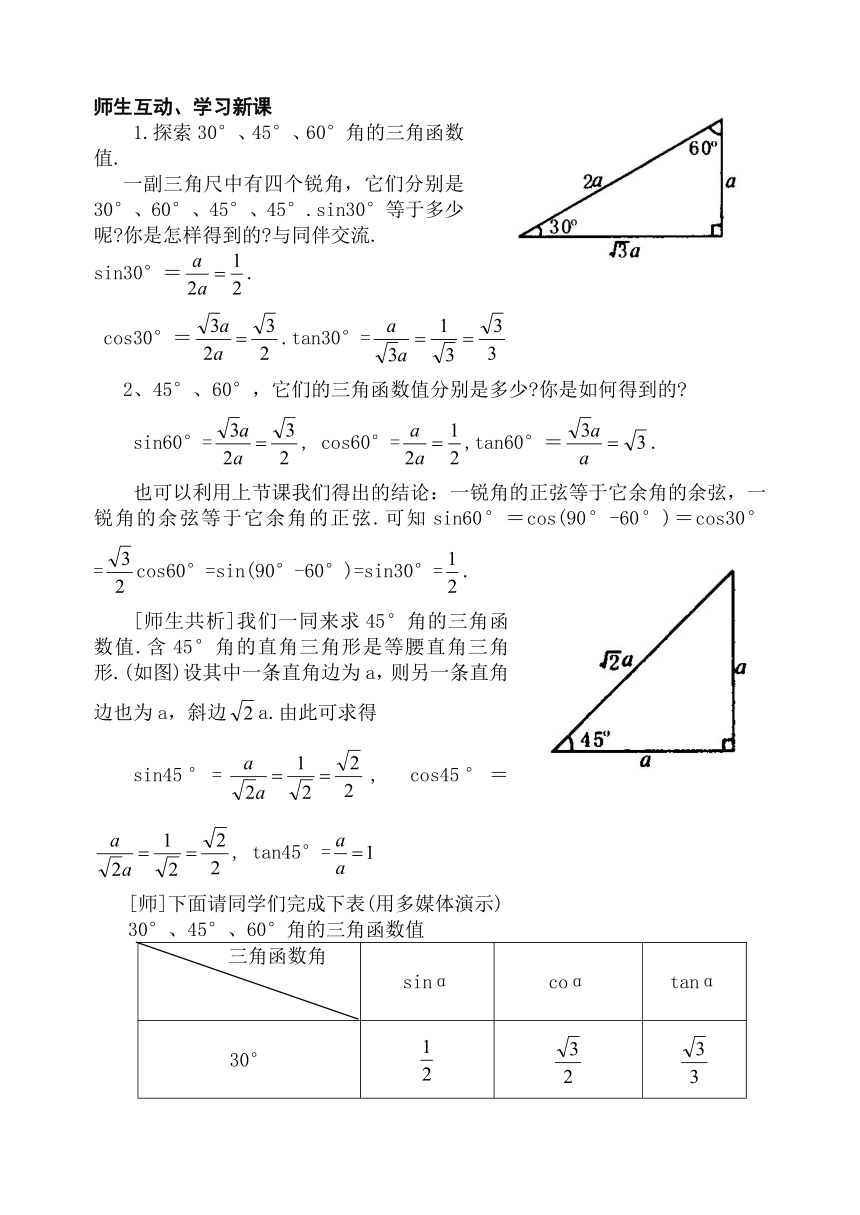
1.探索30°、45°、60°角的三角函数值.
一副三角尺中有四个锐角,它们分别是30°、60°、45°、45°.sin30°等于多少呢 你是怎样得到的 与同伴交流.
sin30°=.
cos30°=.tan30°=
2、45°、60°,它们的三角函数值分别是多少 你是如何得到的
sin60°=, cos60°=,tan60°=.
也可以利用上节课我们得出的结论:一锐角的正弦等于它余角的余弦,一锐角的余弦等于它余角的正弦.可知sin60°=cos(90°-60°)=cos30°=cos60°=sin(90°-60°)=sin30°=.
[师生共析]我们一同来求45°角的三角函数值.含45°角的直角三角形是等腰直角三角形.(如图)设其中一条直角边为a,则另一条直角边也为a,斜边a.由此可求得
sin45°=, cos45°=, tan45°=
[师]下面请同学们完成下表(用多媒体演示)
30°、45°、60°角的三角函数值
三角函数角 sinα coα tanα
30°
45° 1
60°
这个表格中的30°、45°、60°角的三角函数值需熟记,另一方面,要能够根据30°、45°、60°角的三角函数值,说出相应的锐角的大小.
为了帮助大家记忆,我们观察表格中函数值的特点.先看第一列30°、45°、60°角的正弦值,你能发现什么规律呢
2.例题讲解
[例1]计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°.
分析:本题旨在帮助学生巩固特殊角的三角函数值,今后若无特别说明,用特殊角三角函数值进行计算时,一般不取近似值,另外sin260°表示(sin60°)2,cos260°表示
(cos60°)2.
解:(1)sin30°+cos45°=,
(2)sin260°+cos260°-tan45° =()2+()2-1= + -1=0.
[例2]一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差.(结果精确到0.01 m)
分析:引导学生自己根据题意画出示意图,培养学生把实际问题转化为数学问题的能力.
解:根据题意(如图)
可知,∠BOD=60°,OB=OA=OD=2.5 m,∠AOD=×60°=30°,∴OC=OD·cos30°=2.5×≈2.165(m).∴AC=2.5-2.165≈0.34(m).
所以,最高位置与最低位置的高度约为
0.34 m
随堂练习 1.计算:(1)sin60°-tan45°;(2)cos60°+tan60°;
(3) sin45°+sin60°-2cos45°.
解:(1)原式=-1=; (2)原式=+=
(3)原式=×+×;=
2.某商场有一自动扶梯,其倾斜角为30°.高为7 m,扶梯的长度是多少
解:扶梯的长度为=14(m),所以扶梯的长度为14 m.
归纳提炼
本节课总结如下:
(1)探索30°、45°、60°角的三角函数值.
sin30°=,sin45°=,sin60°=;
cos30°=,cos45°= ,cos60°=;
tan30°= ,tan45°=1,tan60°=.
(2)能进行含30°、45°、60°角的三角函数值的计算.
(3)能根据30°、45°、60°角的三角函数值,说出相应锐角的大小.
课后作业
习题1.3第1、2题
活动与探究
(2003年甘肃)如图为住宅区内的两幢楼,它们的高AB=CD=30 m,两楼问的距离AC=24 m,现需了解甲楼对乙楼的采光影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高
(精确到0.1 m,≈1.41,≈1.73)
[过程]根据题意,将实际问题转化为数学问题,当光线从楼顶E,直射到乙楼D点,D点向下便接受不到光线,过D作DB⊥AE(甲楼).在Rt△BDE中.BD=AC=24 m,∠EDB=30°.可求出BE,由于甲、乙楼一样高,所以DF=BE.
[结果]在Kt△BDE中,BE=DB·tan30°=24×=8m.
∵DF=BE,
∴DF=8≈8×1.73=13.84(m).
甲楼的影子在乙楼上的高CD=30-13.84≈16.2(m).
备课资料
参考练习
1.(2003年北京石景山)计算:.
答案:3-
2.(2003年北京崇文)汁算:(+1)-1+2sin30°-
答案:-
3.(2003年广东梅州)计算:(1+)0-|1-sin30°|1+()-1.
答案:
4. (2003 年广西)计算:sin60°+
答案:-
5.(2003年内蒙古赤峰)计算;2-3-(+π)0-cos60°-.
答案:-
教学目标
知识与能力目标
能够进行有关的推理.进一步体会三角函数的意义.会进行30°、45°、60°角的三角函数值的计算.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.
过程与方法目标
通过自主探索经历探索30°、45°、60°角的三角函数值的过程,发展学生观察、分析、发现的能力.培养学生把实际问题转化为数学问题的能力.
情感与价值观要求
通过数学活动,产生好奇心.培养学生独立思考问题的习惯,锻炼克服困难的意志,建立学好数学自信心.
教学重点
探索30°、45°、60°角的三角函数值; 含30°、45°、60°角的三角函数值的计算;锐角三角函数值的大小比较.
教学难点
进一步体会三角函数的意义.
教学过程
创设问题情境,引入新课
[问题]为了测量一棵大树的高度,准备了如下测量工具:①含30°和60°两个锐角的三角尺;②皮尺.请你设计一个测量方案,能测出一棵大树的高度.
让一位同学拿着三角尺站在一个适当的位置B处,使这位同学拿起三角尺,她的视线恰好和斜边重合且过树梢C点,30°的邻边和水平方向平行,用卷尺测出AB的长度,BE的长度,因为DE=AB,所以只需在Rt△CDA中求出CD的长度即可.
提示:在Rt△ACD中,∠CAD=30°,AD=BE,BE是已知的,设BE=a米,则AD=a米,如何求CD呢 含30°角的直角三角形有一个非常重要的性质:30°的角所对的边等于斜边的一半,即AC=2CD,根据勾股定理,(2CD)2=CD2+a2.CD=a.则树的高度即可求出.
[师]我们前面学习了三角函数的定义,如果一个角的大小确定,那么它的正切、正弦、余弦值也随之确定,如果能求出30°的正切值,在上图中,tan30°=,则CD=atan30°,岂不简单.你能求出30°角的三个三角函数值吗
师生互动、学习新课
1.探索30°、45°、60°角的三角函数值.
一副三角尺中有四个锐角,它们分别是30°、60°、45°、45°.sin30°等于多少呢 你是怎样得到的 与同伴交流.
sin30°=.
cos30°=.tan30°=
2、45°、60°,它们的三角函数值分别是多少 你是如何得到的
sin60°=, cos60°=,tan60°=.
也可以利用上节课我们得出的结论:一锐角的正弦等于它余角的余弦,一锐角的余弦等于它余角的正弦.可知sin60°=cos(90°-60°)=cos30°=cos60°=sin(90°-60°)=sin30°=.
[师生共析]我们一同来求45°角的三角函数值.含45°角的直角三角形是等腰直角三角形.(如图)设其中一条直角边为a,则另一条直角边也为a,斜边a.由此可求得
sin45°=, cos45°=, tan45°=
[师]下面请同学们完成下表(用多媒体演示)
30°、45°、60°角的三角函数值
三角函数角 sinα coα tanα
30°
45° 1
60°
这个表格中的30°、45°、60°角的三角函数值需熟记,另一方面,要能够根据30°、45°、60°角的三角函数值,说出相应的锐角的大小.
为了帮助大家记忆,我们观察表格中函数值的特点.先看第一列30°、45°、60°角的正弦值,你能发现什么规律呢
2.例题讲解
[例1]计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°.
分析:本题旨在帮助学生巩固特殊角的三角函数值,今后若无特别说明,用特殊角三角函数值进行计算时,一般不取近似值,另外sin260°表示(sin60°)2,cos260°表示
(cos60°)2.
解:(1)sin30°+cos45°=,
(2)sin260°+cos260°-tan45° =()2+()2-1= + -1=0.
[例2]一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差.(结果精确到0.01 m)
分析:引导学生自己根据题意画出示意图,培养学生把实际问题转化为数学问题的能力.
解:根据题意(如图)
可知,∠BOD=60°,OB=OA=OD=2.5 m,∠AOD=×60°=30°,∴OC=OD·cos30°=2.5×≈2.165(m).∴AC=2.5-2.165≈0.34(m).
所以,最高位置与最低位置的高度约为
0.34 m
随堂练习 1.计算:(1)sin60°-tan45°;(2)cos60°+tan60°;
(3) sin45°+sin60°-2cos45°.
解:(1)原式=-1=; (2)原式=+=
(3)原式=×+×;=
2.某商场有一自动扶梯,其倾斜角为30°.高为7 m,扶梯的长度是多少
解:扶梯的长度为=14(m),所以扶梯的长度为14 m.
归纳提炼
本节课总结如下:
(1)探索30°、45°、60°角的三角函数值.
sin30°=,sin45°=,sin60°=;
cos30°=,cos45°= ,cos60°=;
tan30°= ,tan45°=1,tan60°=.
(2)能进行含30°、45°、60°角的三角函数值的计算.
(3)能根据30°、45°、60°角的三角函数值,说出相应锐角的大小.
课后作业
习题1.3第1、2题
活动与探究
(2003年甘肃)如图为住宅区内的两幢楼,它们的高AB=CD=30 m,两楼问的距离AC=24 m,现需了解甲楼对乙楼的采光影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高
(精确到0.1 m,≈1.41,≈1.73)
[过程]根据题意,将实际问题转化为数学问题,当光线从楼顶E,直射到乙楼D点,D点向下便接受不到光线,过D作DB⊥AE(甲楼).在Rt△BDE中.BD=AC=24 m,∠EDB=30°.可求出BE,由于甲、乙楼一样高,所以DF=BE.
[结果]在Kt△BDE中,BE=DB·tan30°=24×=8m.
∵DF=BE,
∴DF=8≈8×1.73=13.84(m).
甲楼的影子在乙楼上的高CD=30-13.84≈16.2(m).
备课资料
参考练习
1.(2003年北京石景山)计算:.
答案:3-
2.(2003年北京崇文)汁算:(+1)-1+2sin30°-
答案:-
3.(2003年广东梅州)计算:(1+)0-|1-sin30°|1+()-1.
答案:
4. (2003 年广西)计算:sin60°+
答案:-
5.(2003年内蒙古赤峰)计算;2-3-(+π)0-cos60°-.
答案:-
