19.1.2函数的图象(2)
文档属性
| 名称 | 19.1.2函数的图象(2) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-14 23:13:42 | ||
图片预览




文档简介
课件27张PPT。第19章 一次函数19.1.2 函数的图象
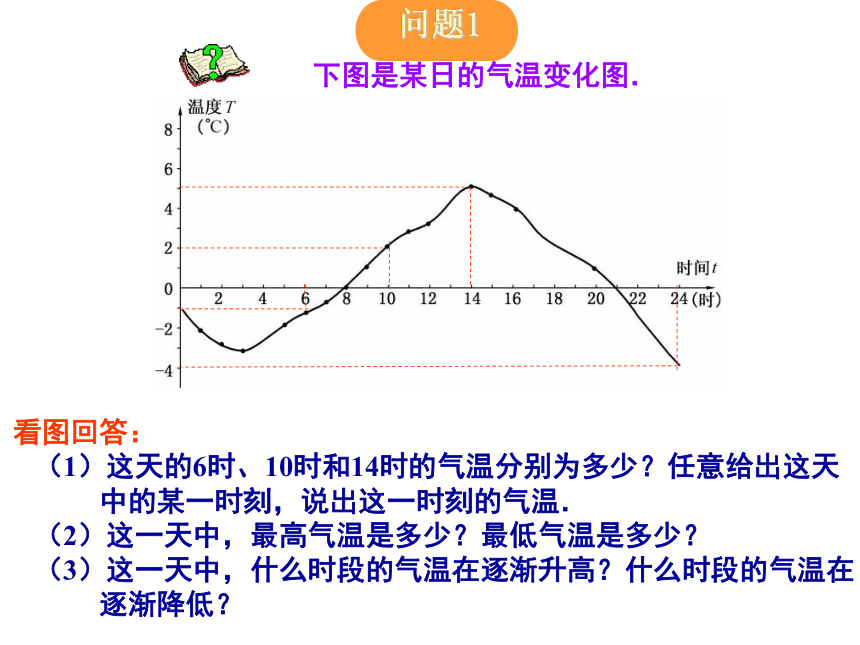
下图是某日的气温变化图.
看图回答:
(1)这天的6时、10时和14时的气温分别为多少?任意给出这天
中的某一时刻,说出这一时刻的气温.
(2)这一天中,最高气温是多少?最低气温是多少?
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在
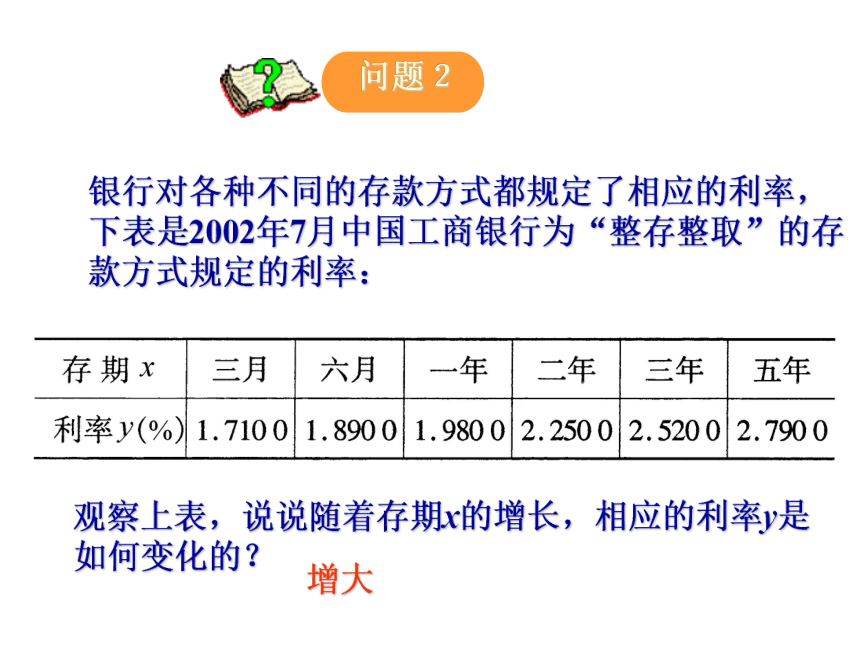
逐渐降低? 银行对各种不同的存款方式都规定了相应的利率,
下表是2002年7月中国工商银行为“整存整取”的存
款方式规定的利率:
观察上表,说说随着存期x的增长,相应的利率y是
如何变化的?
增大
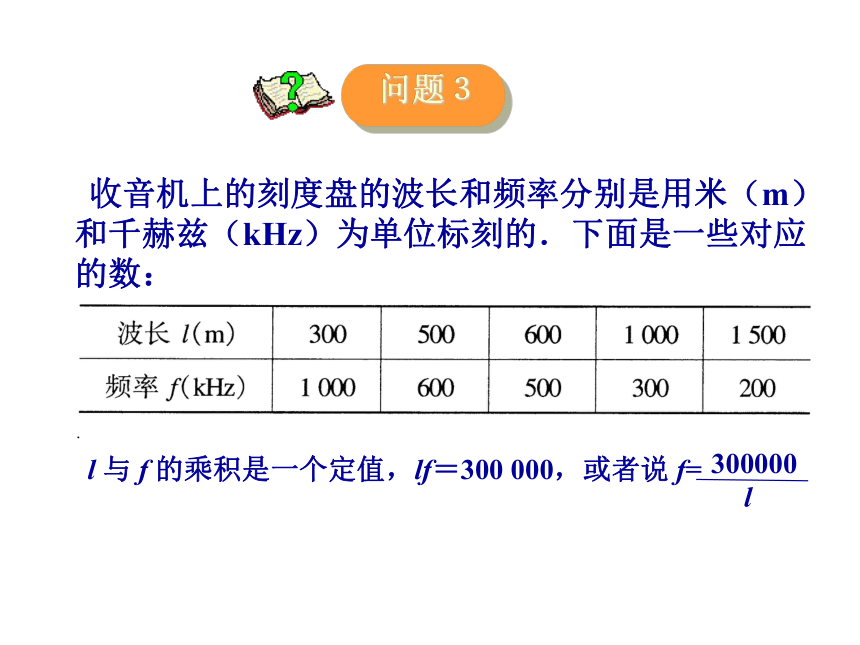
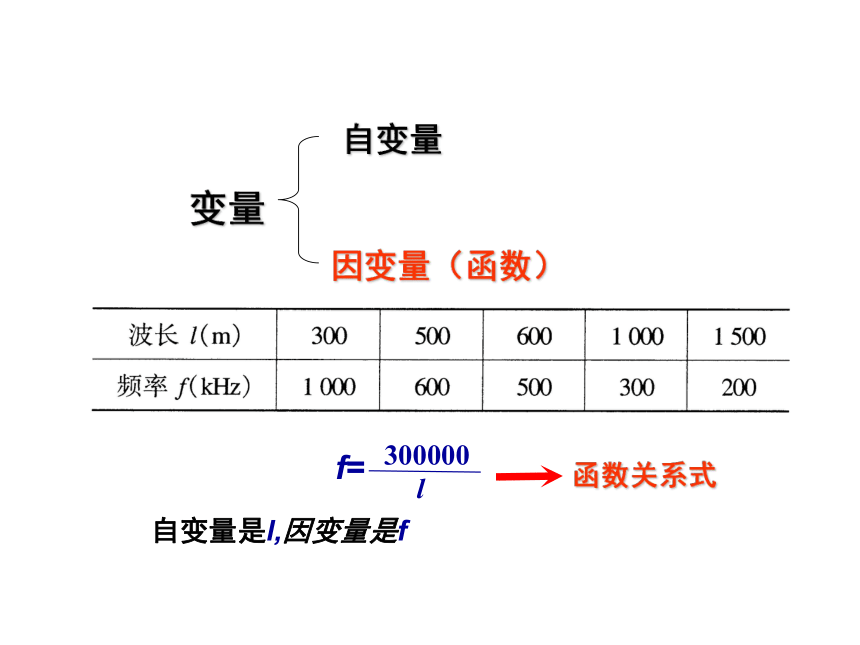
收音机上的刻度盘的波长和频率分别是用米(m)
和千赫兹(kHz)为单位标刻的.下面是一些对应
的数:
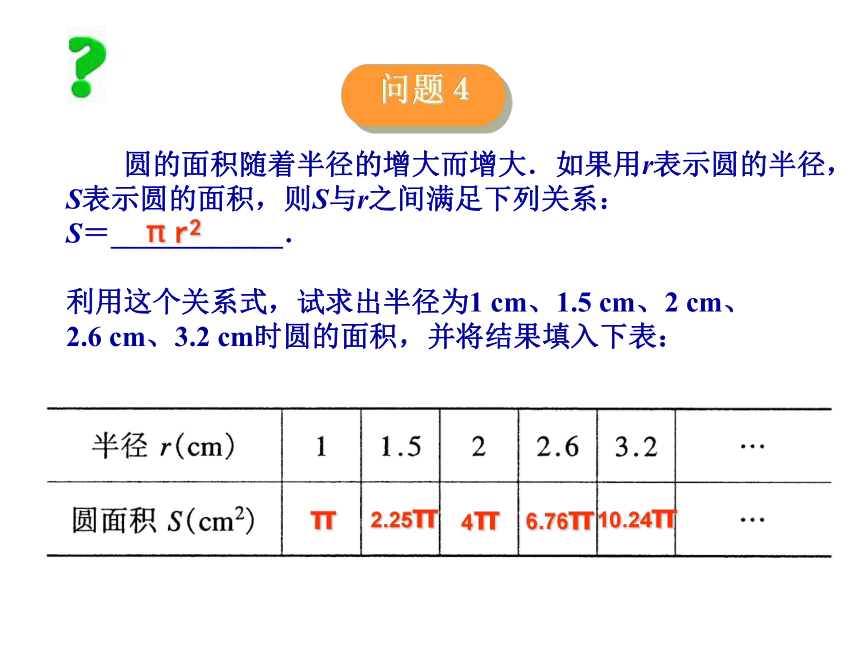
l 与 f 的乘积是一个定值,lf=300 000,或者说 f=. 圆的面积随着半径的增大而增大.如果用r表示圆的半径,
S表示圆的面积,则S与r之间满足下列关系:
S=____________.
利用这个关系式,试求出半径为1 cm、1.5 cm、2 cm、
2.6 cm、3.2 cm时圆的面积,并将结果填入下表:
2.25ππ4π6.76π10.24ππr2变量与常量在某个变化过程中,可以取不同数值的量叫做变量。保持不变的量叫做常量。一、分别指出下列各关系式中的变量与常量:
(1)三角形的一边长5cm,它的面积s(cm)与
这边上的高h(cm)的关系式是s= h;(2)如果直角三角形中一个锐角的度数为α,那
么另一个锐角的度数β与α间的关系式是
β=90-α;(3)如果某种报纸的单价为8元,x表示购买这种
报纸的份数,那么购买报纸的总价y(元)与x
间的关系是y=8x.22 一般地,如果在一个变化过程中,
有两个变量,例如x和y,对于x的每一
个值,y都有惟一的值与之对应,我们
就说x是自变量,y是因变量,此时也
称y是x的函数.结论变量自变量因变量(函数)自变量是l,因变量是f函数关系式(1)半径为R的球的体积为V,则V与R之间的函数关
系为V= πR,此问题中的常量是( );
自变量是( );因变量是( )。(2)桔子每千克售价是2.5元,则购买桔子的数量
P(千克)与所付款Q(元)之间的关系式为
Q=2.5P,此问题中的常量是( ),变
量是( )。二.填空题试一试RV2.5QP三、写出下列各问题中的函数关系式,并指出
其中的常量与变量:(1)圆的周长C与半径r的函数关系式;(2)火车以60千米/时的速度行驶,它驶过
的路程s(千米)与所用时间t(时)的函数关系式;(3)n边形的内角和的度数S与边数n的函数关
系式.写出圆半径r的关于圆面积S的函数关系式?若要画一个面积为10 圆,圆的半径应取多少?若圆的面积为20 呢? 圆面积公式 面积为10 的圆半径 ≈ 1.78(cm) 面积为20 的圆半径 ≈ 2.52(cm) 函数关系式为 随堂练习:随堂练习:VRQ=40-5t其中自变量是 , 是 的函数
其中自变量的取值范围是 .2.汽车开始行使时油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q升与行使时间t小时的函数解析式是 . 其中自变量是 , Q是t的 .当t=8时,函数值为 .自变量t的取值范围是 .t函数RR>003.一个三角形的底边长5cm,.写出面积S随h变化的函数关系式,并指出其中的自变量和它的取值范围.解:自变量是 hh >0 4.夏季高山上温度从山脚起每升高100米降低 0.6℃,已知山脚下温度是23℃,则温度y与上升高度 x之间的函数关系式 ,若某种植物适宜生长的度为170c中的自变量与函数。(1)一个正方形的边长为3cm,它的各边长减少
xcm后,得到的新正方形的周长为ycm,求y
与x之间的函数关系式;(2)寄一封重量在20克以内的市内平信,需邮资
0.60元,求寄n封信所需邮资y(元)与n间的
函数关系式;课后作业:2.小红的爷爷饭后出去散步,从家里出发走20分钟到
一个离家900米的街心花园与朋友聊天10分钟后,用15
分钟返回家里.下面图形中表示小红爷爷离家距离y(米)
与时间x(分)之间函数关系的是( )AD(1) y=2x+1 (2)(3)(4)(5)记 一 记确定函数自变量取值范围的条件:(1)分母不等于0;【 (a≠ 0】
(2)开偶数次方中的被开方数必须大于等于0。【 (a≥0】求下列函数的自变量x的取值范围:(x≠0)(x≠-1)(x≥0)(x为一切实数)(x≥2)(x为一切实数)练 习求下面的函数自变量的取值范围:5想想下面这几道题——看谁做的快而准求下列各函数的自变量x的取值范围。(1)(2)(3)(4)(5)3小结 从现实问题出发,寻求事物变化中变量之间变化规律的一般方法及步骤:1.确定事物变化中的变量与常量.2.尝试运算寻求变量间存在的规律.3.利用学过的有关知识确定函数关系式.4.根据实际意义及函数关系式的特点确定自变量的取值范围.
下图是某日的气温变化图.
看图回答:
(1)这天的6时、10时和14时的气温分别为多少?任意给出这天
中的某一时刻,说出这一时刻的气温.
(2)这一天中,最高气温是多少?最低气温是多少?
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在
逐渐降低? 银行对各种不同的存款方式都规定了相应的利率,
下表是2002年7月中国工商银行为“整存整取”的存
款方式规定的利率:
观察上表,说说随着存期x的增长,相应的利率y是
如何变化的?
增大
收音机上的刻度盘的波长和频率分别是用米(m)
和千赫兹(kHz)为单位标刻的.下面是一些对应
的数:
l 与 f 的乘积是一个定值,lf=300 000,或者说 f=. 圆的面积随着半径的增大而增大.如果用r表示圆的半径,
S表示圆的面积,则S与r之间满足下列关系:
S=____________.
利用这个关系式,试求出半径为1 cm、1.5 cm、2 cm、
2.6 cm、3.2 cm时圆的面积,并将结果填入下表:
2.25ππ4π6.76π10.24ππr2变量与常量在某个变化过程中,可以取不同数值的量叫做变量。保持不变的量叫做常量。一、分别指出下列各关系式中的变量与常量:
(1)三角形的一边长5cm,它的面积s(cm)与
这边上的高h(cm)的关系式是s= h;(2)如果直角三角形中一个锐角的度数为α,那
么另一个锐角的度数β与α间的关系式是
β=90-α;(3)如果某种报纸的单价为8元,x表示购买这种
报纸的份数,那么购买报纸的总价y(元)与x
间的关系是y=8x.22 一般地,如果在一个变化过程中,
有两个变量,例如x和y,对于x的每一
个值,y都有惟一的值与之对应,我们
就说x是自变量,y是因变量,此时也
称y是x的函数.结论变量自变量因变量(函数)自变量是l,因变量是f函数关系式(1)半径为R的球的体积为V,则V与R之间的函数关
系为V= πR,此问题中的常量是( );
自变量是( );因变量是( )。(2)桔子每千克售价是2.5元,则购买桔子的数量
P(千克)与所付款Q(元)之间的关系式为
Q=2.5P,此问题中的常量是( ),变
量是( )。二.填空题试一试RV2.5QP三、写出下列各问题中的函数关系式,并指出
其中的常量与变量:(1)圆的周长C与半径r的函数关系式;(2)火车以60千米/时的速度行驶,它驶过
的路程s(千米)与所用时间t(时)的函数关系式;(3)n边形的内角和的度数S与边数n的函数关
系式.写出圆半径r的关于圆面积S的函数关系式?若要画一个面积为10 圆,圆的半径应取多少?若圆的面积为20 呢? 圆面积公式 面积为10 的圆半径 ≈ 1.78(cm) 面积为20 的圆半径 ≈ 2.52(cm) 函数关系式为 随堂练习:随堂练习:VRQ=40-5t其中自变量是 , 是 的函数
其中自变量的取值范围是 .2.汽车开始行使时油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q升与行使时间t小时的函数解析式是 . 其中自变量是 , Q是t的 .当t=8时,函数值为 .自变量t的取值范围是 .t函数RR>003.一个三角形的底边长5cm,.写出面积S随h变化的函数关系式,并指出其中的自变量和它的取值范围.解:自变量是 hh >0 4.夏季高山上温度从山脚起每升高100米降低 0.6℃,已知山脚下温度是23℃,则温度y与上升高度 x之间的函数关系式 ,若某种植物适宜生长的度为170c
xcm后,得到的新正方形的周长为ycm,求y
与x之间的函数关系式;(2)寄一封重量在20克以内的市内平信,需邮资
0.60元,求寄n封信所需邮资y(元)与n间的
函数关系式;课后作业:2.小红的爷爷饭后出去散步,从家里出发走20分钟到
一个离家900米的街心花园与朋友聊天10分钟后,用15
分钟返回家里.下面图形中表示小红爷爷离家距离y(米)
与时间x(分)之间函数关系的是( )AD(1) y=2x+1 (2)(3)(4)(5)记 一 记确定函数自变量取值范围的条件:(1)分母不等于0;【 (a≠ 0】
(2)开偶数次方中的被开方数必须大于等于0。【 (a≥0】求下列函数的自变量x的取值范围:(x≠0)(x≠-1)(x≥0)(x为一切实数)(x≥2)(x为一切实数)练 习求下面的函数自变量的取值范围:5想想下面这几道题——看谁做的快而准求下列各函数的自变量x的取值范围。(1)(2)(3)(4)(5)3小结 从现实问题出发,寻求事物变化中变量之间变化规律的一般方法及步骤:1.确定事物变化中的变量与常量.2.尝试运算寻求变量间存在的规律.3.利用学过的有关知识确定函数关系式.4.根据实际意义及函数关系式的特点确定自变量的取值范围.
