19.2.2一次函数(3)
文档属性
| 名称 | 19.2.2一次函数(3) |  | |
| 格式 | zip | ||
| 文件大小 | 262.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-14 23:29:11 | ||
图片预览






文档简介
课件21张PPT。19.2.2 一次函数(3)第19章 一次函数 1、学会用待定系数法确定
一次函数解析式.学习目标 2、具体感知数形结合思想
在一次函数中的应用. 3、利用一次函数知识解决
相关实际问题.一.旧知识回顾1,填空题:(1)若点A(-1,1)在函数y=kx的图象上则k=
(2)在一次函数y=kx-3中,当x=3时
y=6则k=
(3)一次函数y=3x-b过A(-2,1)则b=-13-7例解方程组:①②解:由①,得x=7-y ③ 把③代入②,得3×(7-y)+y=17解得,y =2把y =2代入③,得x =7-2=5∴原方程组的解是:解: 由②式- ①式得 2x=10解得 x=5把x=5代入①式得 y =2
∴原方程组的解是:
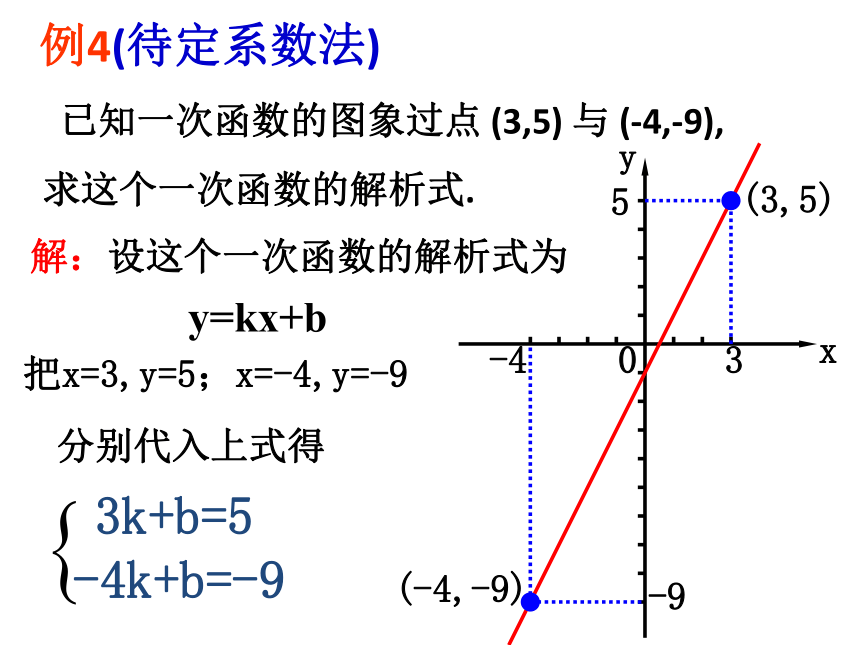
例4(待定系数法) 已知一次函数的图象过点 (3,5) 与 (-4,-9),
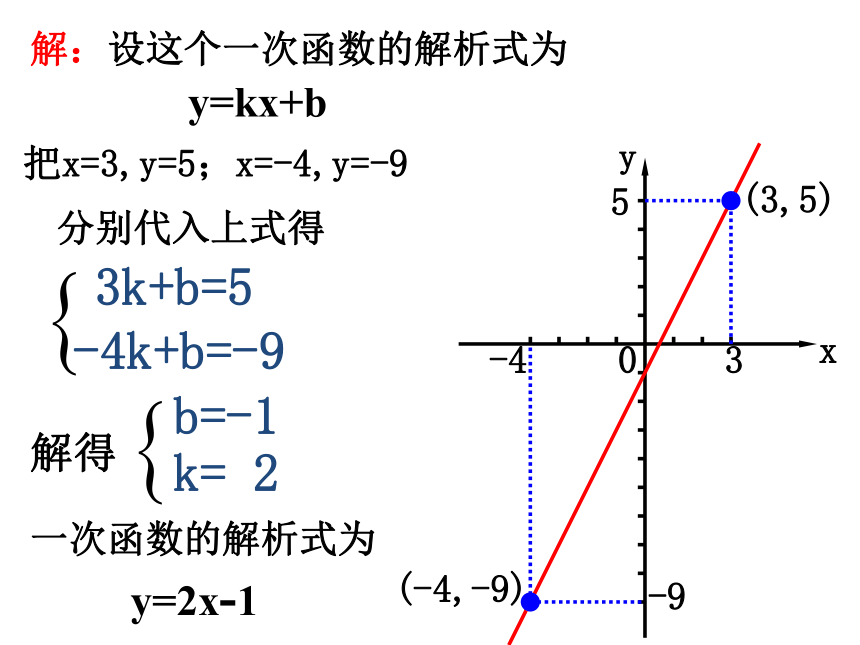
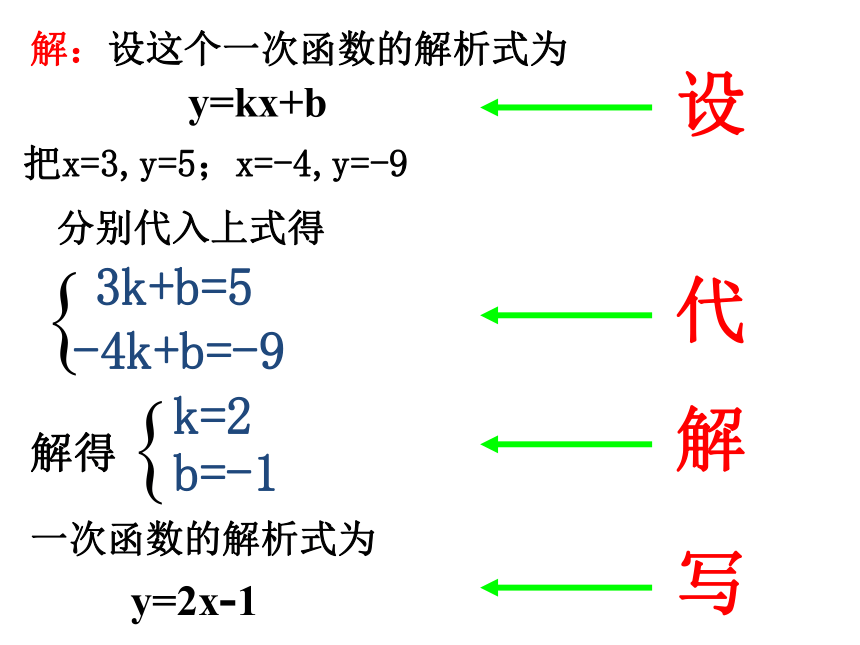
求这个一次函数的解析式.35-4-9解:设这个一次函数的解析式为y=kx+b把x=3,y=5;x=-4,y=-93k+b=5 分别代入上式得-4k+b=-9解得一次函数的解析式为y=2x-1设代解写解题的四个步骤:第一步:设,设出函数的一般形式。(称一次函数的通式)第二步:代,代入解析式得出方程或方程组。第三步:求,通过列方程或方程组求出待定系数k,b的值。第四步:写,写出该函数的解析式。3.练习:
(1)已知一次函数的图象经过点(1,-1)和点(-1,2)。求这个函数的解析式。
(2)已知一次函数y=kx+b中,当x=1时,y=3,当x=-1时,y=7。求这个函数的解析式。且求当x=3时,y的值。
(3)师:已知直线上两点坐标,能求出这条直线的解析式,若不直接告诉两点的坐标,已知这条直线的图象,能否求出它的解析式?
如:
1)已知一次函数的图象经过点(1,-1)和点(-1,2)。求这个函数的解析式。
解:设这个一次函数的解析式为:y=kx+b
把x=1,y=-1;x=-1,y=2,分别代入上式得
﹛K+b=-1
-k+b=2
解得:﹛K=b=一次函数的解析式为:y= x(2)解:把x=1,y=3;x=-1,y=7,分别代入上y=kx+b得
﹛K+b=3-k+b=7解得:﹛K=-2b=5一次函数的解析式为:y=-2x+5
当x=3时 y=-2*3+5=-1 所以的值y=-1(3),解:由题意已知一次函数的图象经过点(2,0)和点(0,-3)设这个一次函数的解析为:y=kx+b
把x=2,y=0;x=0,y=-3,分别代入上式得
﹛2k+b=0b=-3解得:﹛K=b=-3一次函数的解析式为:y= x-3例2:已知弹簧长度y(厘米)在一定限度内所挂重物质量x(千克)的一次函数,现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的解析时。解:设这个一次函数的解析式为:y=kx+b
根据题意,得﹛b=64k+b=7.2解这个方程组,得﹛b=6k=0.3所以一次函数的解析式为:y=0.3x+6
(1)一次函数的图象经过点(2,1)和(1,5),则这个一次函数( )
A.y=4x+9 B. y=4x-9 C. y=-4x+9 D. y=-4x-9(2)已知点P的横坐标与纵坐标之和为1,且这点在直线y=x+3上,则该点是( )
A.(-7,8) B. (-5,6) C. (-4,5) D. (-1,2)
(3)若点A(-4,0)、B(0,5)、C(m,-5)在同一条直线上,则m的值是( )
A.8 B.4 C.-6 D.-8
1、选择题CADD尝试练习3.一次函数y=kx+5与直线y=2x-1交于点P(2,m),求k、m的值.4.一次函数y=3x-b过A(-2,1)则b= ,该图象经过点B( ,-1)和点C(0, ).5.已知函数y=kx+b的图象与另一个一次函数y=-2x-1的图象相交于y轴上的点A,且x轴下方的一点B(3,n)在一次函数y=kx+b的图象上,n满足关系n2=9.求这个函数的解析式.回顾与小结本节课里你学到了什么???(1)会用待定系数法求函数的解析式.(2)一次函数图象的性质及其应用
一次函数解析式.学习目标 2、具体感知数形结合思想
在一次函数中的应用. 3、利用一次函数知识解决
相关实际问题.一.旧知识回顾1,填空题:(1)若点A(-1,1)在函数y=kx的图象上则k=
(2)在一次函数y=kx-3中,当x=3时
y=6则k=
(3)一次函数y=3x-b过A(-2,1)则b=-13-7例解方程组:①②解:由①,得x=7-y ③ 把③代入②,得3×(7-y)+y=17解得,y =2把y =2代入③,得x =7-2=5∴原方程组的解是:解: 由②式- ①式得 2x=10解得 x=5把x=5代入①式得 y =2
∴原方程组的解是:
例4(待定系数法) 已知一次函数的图象过点 (3,5) 与 (-4,-9),
求这个一次函数的解析式.35-4-9解:设这个一次函数的解析式为y=kx+b把x=3,y=5;x=-4,y=-93k+b=5 分别代入上式得-4k+b=-9解得一次函数的解析式为y=2x-1设代解写解题的四个步骤:第一步:设,设出函数的一般形式。(称一次函数的通式)第二步:代,代入解析式得出方程或方程组。第三步:求,通过列方程或方程组求出待定系数k,b的值。第四步:写,写出该函数的解析式。3.练习:
(1)已知一次函数的图象经过点(1,-1)和点(-1,2)。求这个函数的解析式。
(2)已知一次函数y=kx+b中,当x=1时,y=3,当x=-1时,y=7。求这个函数的解析式。且求当x=3时,y的值。
(3)师:已知直线上两点坐标,能求出这条直线的解析式,若不直接告诉两点的坐标,已知这条直线的图象,能否求出它的解析式?
如:
1)已知一次函数的图象经过点(1,-1)和点(-1,2)。求这个函数的解析式。
解:设这个一次函数的解析式为:y=kx+b
把x=1,y=-1;x=-1,y=2,分别代入上式得
﹛K+b=-1
-k+b=2
解得:﹛K=b=一次函数的解析式为:y= x(2)解:把x=1,y=3;x=-1,y=7,分别代入上y=kx+b得
﹛K+b=3-k+b=7解得:﹛K=-2b=5一次函数的解析式为:y=-2x+5
当x=3时 y=-2*3+5=-1 所以的值y=-1(3),解:由题意已知一次函数的图象经过点(2,0)和点(0,-3)设这个一次函数的解析为:y=kx+b
把x=2,y=0;x=0,y=-3,分别代入上式得
﹛2k+b=0b=-3解得:﹛K=b=-3一次函数的解析式为:y= x-3例2:已知弹簧长度y(厘米)在一定限度内所挂重物质量x(千克)的一次函数,现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的解析时。解:设这个一次函数的解析式为:y=kx+b
根据题意,得﹛b=64k+b=7.2解这个方程组,得﹛b=6k=0.3所以一次函数的解析式为:y=0.3x+6
(1)一次函数的图象经过点(2,1)和(1,5),则这个一次函数( )
A.y=4x+9 B. y=4x-9 C. y=-4x+9 D. y=-4x-9(2)已知点P的横坐标与纵坐标之和为1,且这点在直线y=x+3上,则该点是( )
A.(-7,8) B. (-5,6) C. (-4,5) D. (-1,2)
(3)若点A(-4,0)、B(0,5)、C(m,-5)在同一条直线上,则m的值是( )
A.8 B.4 C.-6 D.-8
1、选择题CADD尝试练习3.一次函数y=kx+5与直线y=2x-1交于点P(2,m),求k、m的值.4.一次函数y=3x-b过A(-2,1)则b= ,该图象经过点B( ,-1)和点C(0, ).5.已知函数y=kx+b的图象与另一个一次函数y=-2x-1的图象相交于y轴上的点A,且x轴下方的一点B(3,n)在一次函数y=kx+b的图象上,n满足关系n2=9.求这个函数的解析式.回顾与小结本节课里你学到了什么???(1)会用待定系数法求函数的解析式.(2)一次函数图象的性质及其应用
