19.2.2一次函数(4)
文档属性
| 名称 | 19.2.2一次函数(4) |  | |
| 格式 | zip | ||
| 文件大小 | 464.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-14 23:29:29 | ||
图片预览



文档简介
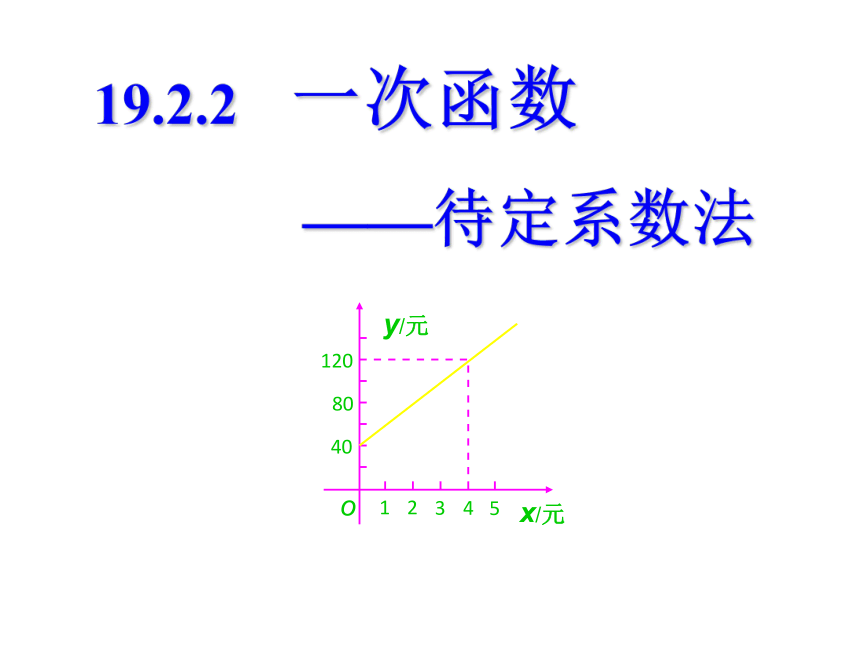
课件19张PPT。19.2.2 一次函数(4)第19章 一次函数19.2.2 一次函数
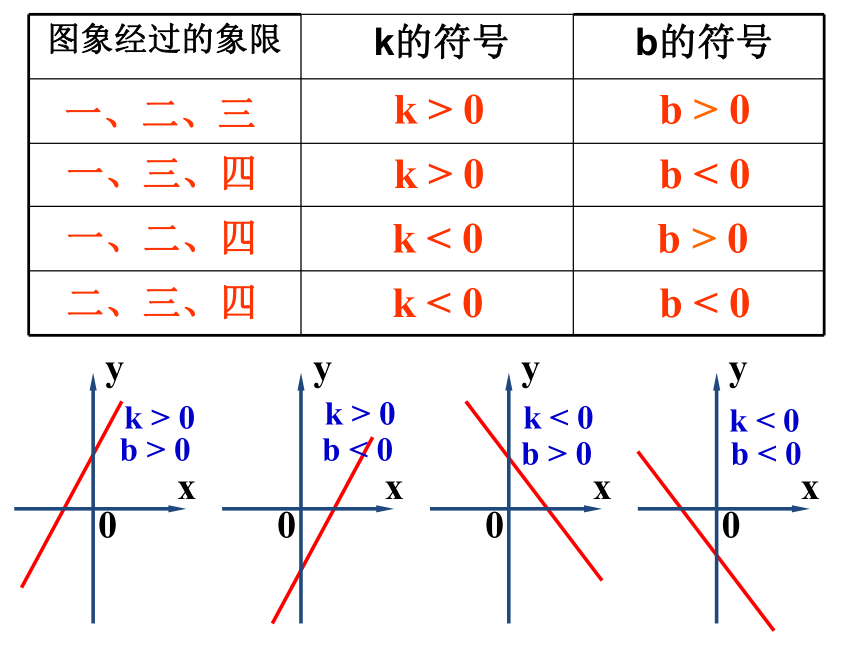
——待定系数法 k > 0 k < 0一、二、三一、三、四一、二、四二、三、四 k > 0 k < 0 b < 0 b < 0 b > 0 b > 0 k > 0 k > 0 k < 0 k < 0 b < 0 b < 0 b > 0 b > 0思考:过点(3,5)与(4,9)的直线是一次函数y=2x-1的图像吗?
问题:反之,若一次函数的图像过点(3,5)与(4,9),则这个函数的解析式是y=2x-1吗?若是,又是怎么样得到的呢?
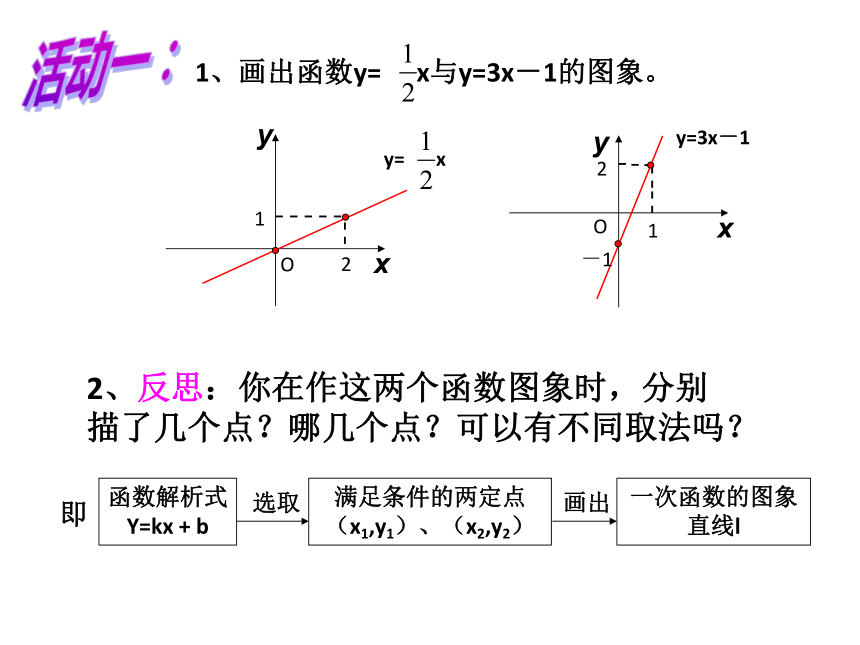
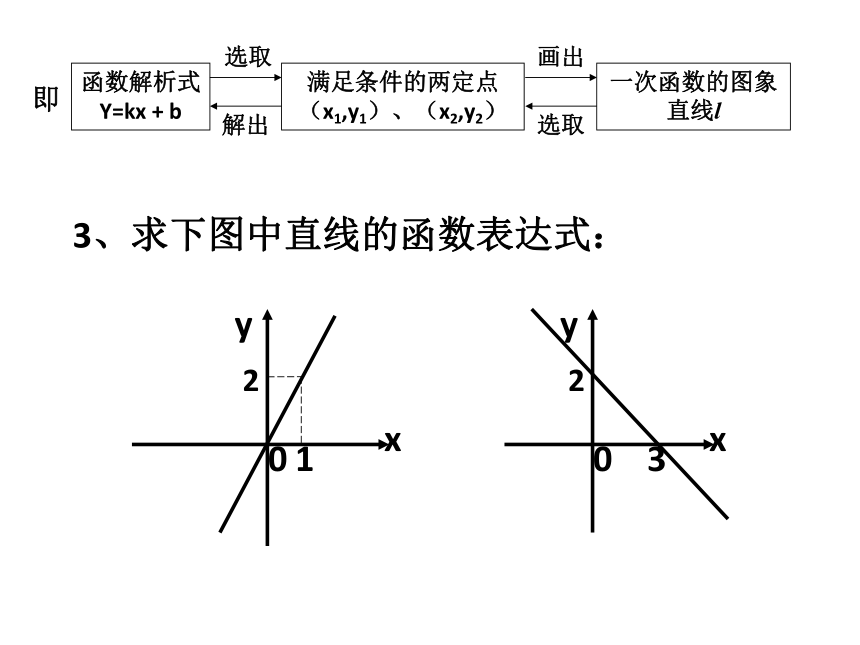
2、反思:你在作这两个函数图象时,分别描了几个点?哪几个点?可以有不同取法吗?活动一:1、画出函数y= x与y=3x-1的图象。3、求下图中直线的函数表达式:例1 已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式。利用待定系数法求一次函数的一般步骤为:1.设出函数的解析式y=kx+b(k≠0); 议一议:知识导学:2.根据条件列出关于k、b的二元一次方程组;3.解方程组,求出k、b的值,
4.写出一次函数的解析式。解:设一次函数解析式为y=kx+b(k≠0),
把x=1时, y=5;x=6时,y=0代入解析式,得解得∴一次函数的解析式为 y= - x+6。例2、已知一次函数在x=1 时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式。y=2x-41、已知一个正比例函数的图象过(1,2),则这个函数的解析式是_____。2、已知一次函数y=kx+2,当x=2时,y的值为8,则这个函数的解析式是_____,
当x=-2时,y=_____。3、老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:甲:函数的图象经过第一象限;乙、函数的图象经过第二象限;丙、在每个象限内,y随x的增大而增大。
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数关系式:________活动二:y=3x+24.若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( )
A (-1,1) B (2,2)
C (-2,2) D (2,一2) B5、若直线y=kx+b平行直线y=-3x+2,且在y轴上的的截距为-5,则k= ,b= 。-3-56、在直角坐标系中,一次函数y=kx+b的图像经过三点A(2,0)、B(0,2)、C(m,3),求这个函数的关系式,并求m的值。 7、已知一次函数的图像经过点A(2,-1)和点B,其中点B是另一条直线 与
y轴的交点,求这个一次函数的表达式。例3 已知2y-3与3x+1成正比例,且当x=2时,y=5
(1) 求y与x之间的函数解析式,并指出它是什么函数?
(2) 若点(a,2)在这个函数的图像上,求a的值。例4 小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式。
(2)根据关系式计算,小明经过几个月才能存够200元?解: (1)设函数解析式为y=kx+b(k≠0),由图可知图象过(0,40)、(4,120)∴解析式为y=20x+40 (x≥0)(2)当y=200时,20x+40=200, x=8∴小明经过8个月才能存够200元解之得∴ 正处在花季的同学们,随着身体的发育,身高的不断升高,所穿的鞋码也在不断地变大。研究表明鞋码y(码)是脚长x(cm)(指脚底的长度)的一次函数。某班学生对鞋子的鞋码与脚长进行调查,获得如下数据:(1)求出y与x之间的函数关系式。(不要求写出自变量x的取值范围)
(2)某人穿38码的鞋,则他的脚长是多少?若脚长为25厘米应穿多少码呢?知识应用:(1)求出y与x之间的函数关系式。(不要求写出自变量x的取值范围)
(2)某人穿38码的鞋,则他的脚长是多少?若脚长为25厘米应穿多少码呢?解:(1)设函数解析式为y=kx+b (k≠0) ,由表知,把(22,34)、(23,36)代入得解之得∴解析式为y=2x-10当x=25时,y=2x25-10=40, (2)由表可知某人穿38码的鞋,他的脚长是24cm∴脚长为25厘米应穿40码如图,在平面直角坐标系内,一次函数y=kx + b的图象分别与x轴和直线x=4交于点A、B,直线x=4与x轴交于点C,△ABC的面积为10,若A的横坐标为-1,求这个一次函数的解析式。知识拓展:2. 沙尘暴发生后,经过开阔荒漠时加速,经过乡镇、遇到防护林带区则减速,最终停止。某气象研究所观察一场沙尘暴从发生到结束的全过程,记录了风速y(km/h)随时间t(h)变化的图象(如图)
(1)??? 求沙尘暴的最大风速;
(2)????用恰当的方式表示沙尘暴风速y与时间t之间的关系。共同回顾:再 见
——待定系数法 k > 0 k < 0一、二、三一、三、四一、二、四二、三、四 k > 0 k < 0 b < 0 b < 0 b > 0 b > 0 k > 0 k > 0 k < 0 k < 0 b < 0 b < 0 b > 0 b > 0思考:过点(3,5)与(4,9)的直线是一次函数y=2x-1的图像吗?
问题:反之,若一次函数的图像过点(3,5)与(4,9),则这个函数的解析式是y=2x-1吗?若是,又是怎么样得到的呢?
2、反思:你在作这两个函数图象时,分别描了几个点?哪几个点?可以有不同取法吗?活动一:1、画出函数y= x与y=3x-1的图象。3、求下图中直线的函数表达式:例1 已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式。利用待定系数法求一次函数的一般步骤为:1.设出函数的解析式y=kx+b(k≠0); 议一议:知识导学:2.根据条件列出关于k、b的二元一次方程组;3.解方程组,求出k、b的值,
4.写出一次函数的解析式。解:设一次函数解析式为y=kx+b(k≠0),
把x=1时, y=5;x=6时,y=0代入解析式,得解得∴一次函数的解析式为 y= - x+6。例2、已知一次函数在x=1 时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式。y=2x-41、已知一个正比例函数的图象过(1,2),则这个函数的解析式是_____。2、已知一次函数y=kx+2,当x=2时,y的值为8,则这个函数的解析式是_____,
当x=-2时,y=_____。3、老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:甲:函数的图象经过第一象限;乙、函数的图象经过第二象限;丙、在每个象限内,y随x的增大而增大。
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数关系式:________活动二:y=3x+24.若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( )
A (-1,1) B (2,2)
C (-2,2) D (2,一2) B5、若直线y=kx+b平行直线y=-3x+2,且在y轴上的的截距为-5,则k= ,b= 。-3-56、在直角坐标系中,一次函数y=kx+b的图像经过三点A(2,0)、B(0,2)、C(m,3),求这个函数的关系式,并求m的值。 7、已知一次函数的图像经过点A(2,-1)和点B,其中点B是另一条直线 与
y轴的交点,求这个一次函数的表达式。例3 已知2y-3与3x+1成正比例,且当x=2时,y=5
(1) 求y与x之间的函数解析式,并指出它是什么函数?
(2) 若点(a,2)在这个函数的图像上,求a的值。例4 小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式。
(2)根据关系式计算,小明经过几个月才能存够200元?解: (1)设函数解析式为y=kx+b(k≠0),由图可知图象过(0,40)、(4,120)∴解析式为y=20x+40 (x≥0)(2)当y=200时,20x+40=200, x=8∴小明经过8个月才能存够200元解之得∴ 正处在花季的同学们,随着身体的发育,身高的不断升高,所穿的鞋码也在不断地变大。研究表明鞋码y(码)是脚长x(cm)(指脚底的长度)的一次函数。某班学生对鞋子的鞋码与脚长进行调查,获得如下数据:(1)求出y与x之间的函数关系式。(不要求写出自变量x的取值范围)
(2)某人穿38码的鞋,则他的脚长是多少?若脚长为25厘米应穿多少码呢?知识应用:(1)求出y与x之间的函数关系式。(不要求写出自变量x的取值范围)
(2)某人穿38码的鞋,则他的脚长是多少?若脚长为25厘米应穿多少码呢?解:(1)设函数解析式为y=kx+b (k≠0) ,由表知,把(22,34)、(23,36)代入得解之得∴解析式为y=2x-10当x=25时,y=2x25-10=40, (2)由表可知某人穿38码的鞋,他的脚长是24cm∴脚长为25厘米应穿40码如图,在平面直角坐标系内,一次函数y=kx + b的图象分别与x轴和直线x=4交于点A、B,直线x=4与x轴交于点C,△ABC的面积为10,若A的横坐标为-1,求这个一次函数的解析式。知识拓展:2. 沙尘暴发生后,经过开阔荒漠时加速,经过乡镇、遇到防护林带区则减速,最终停止。某气象研究所观察一场沙尘暴从发生到结束的全过程,记录了风速y(km/h)随时间t(h)变化的图象(如图)
(1)??? 求沙尘暴的最大风速;
(2)????用恰当的方式表示沙尘暴风速y与时间t之间的关系。共同回顾:再 见
