19.2.2一次函数(7)
文档属性
| 名称 | 19.2.2一次函数(7) |  | |
| 格式 | zip | ||
| 文件大小 | 116.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-14 23:30:17 | ||
图片预览





文档简介
课件15张PPT。19.2.2 一次函数(7)第19章 一次函数(1)解不等式5x+6>3x+10.问题:(2) 函数y=2x-4的图象与x轴的交
点坐标是_____;当x>2时,y的取值
有何特点?x<2呢?函数与y轴的交
点坐标是_____;当y>-4时,x的取
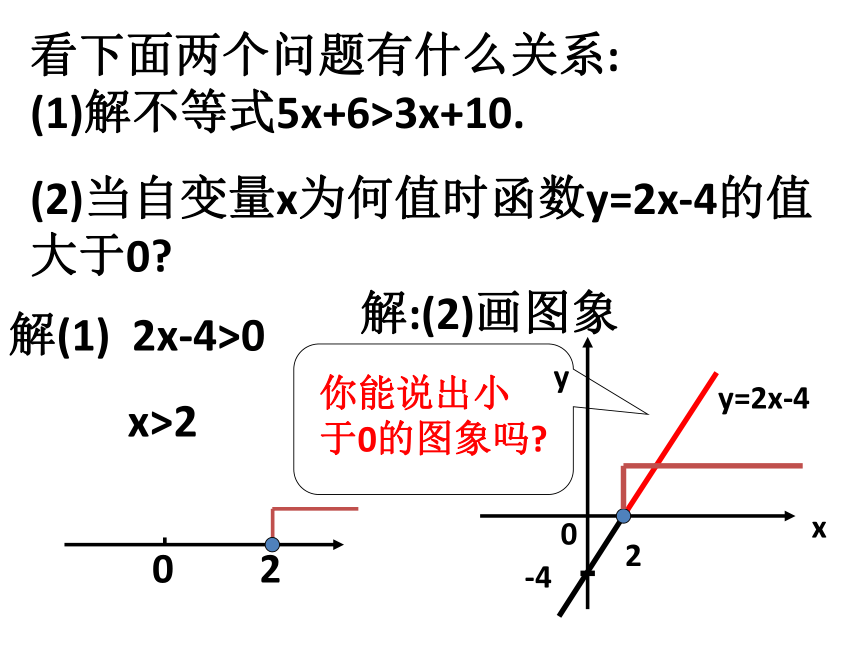
值有何特点?y<-4呢?(2,0)(0,-4)看下面两个问题有什么关系:(1)解不等式5x+6>3x+10.
(2)当自变量x为何值时函数y=2x-4的值大于0?解(1) 2x-4>0
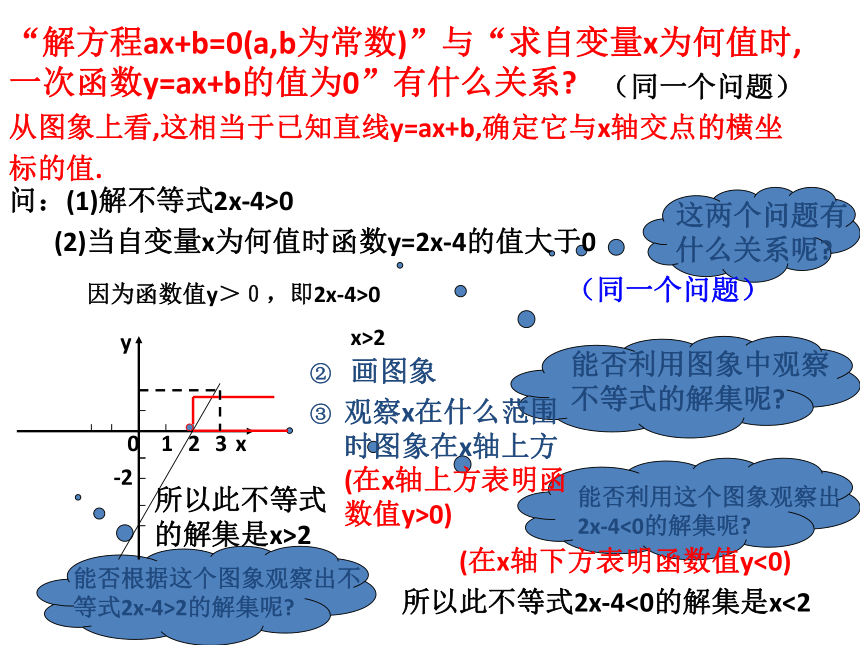
x>2解:(2)画图象2-4y=2x-40yx“解方程ax+b=0(a,b为常数)”与“求自变量x为何值时,一次函数y=ax+b的值为0”有什么关系?(同一个问题)问:(1)解不等式2x-4>0
(2)当自变量x为何值时函数y=2x-4的值大于0这两个问题有什么关系呢?因为函数值y>0,即2x-4>0
x>2(同一个问题)能否利用图象中观察不等式的解集呢?从图象上看,这相当于已知直线y=ax+b,确定它与x轴交点的横坐
标的值.画图象②观察x在什么范围时图象在x轴上方③(在x轴上方表明函数值y>0)所以此不等式的解集是x>2能否利用这个图象观察出2x-4<0的解集呢?(在x轴下方表明函数值y<0)所以此不等式2x-4<0的解集是x<2能否根据这个图象观察出不等式2x-4>2的解集呢?3“解方程ax+b=0(a,b为常数,a≠0)”与“求自变量x为何值时,一次函数y=ax+b的值为0”有什么关系?4“解不等式ax+b>0(a,b为常数,a≠0)”与“求自变量x为什么范围内,一次函数y=ax+b的值大于0”有什么关系?(同一个问题)由于任何一元一次不等式都可以转化为ax+b>0或ax<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数大(小)于0时,求自变量的相应的取值范围.探究归纳:
任何不等式都可以转化为ax+b>0或ax+b<0(a,ba≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大(小)于0时,求自变量相应的取值范围利用图象求不等式6x-3<x+2的解方法一:将方程变形为ax+b<0的形式5x-5<0转化为函数解析式画图象y=5x-5方法二:把不等式6x-3<x+2的两边看成是两个函数:即y1=6x-3,y2=x+2转化为两个函数画出两个函数图象找出交点(观察x在什么范围时图象y1点在y2点的下方)0-1yx1所以不等式6x-3<x+2的解是x<1所以不等式6x-3<x+2的解是x<1(观察x在什么范围时图象上的点是x轴下方)例2用画函数图像的方法解不等式5x+4<2x+10解法1:设y=3x-6并画出图像y-6x20解法1:设y1=5x+4;y2=2x+10并画出图像练习:
1、当自变量x的取值满足什么条件时,函数y=3x+8的值满足下列条件?
(1)y>0 (2)y<2
2、利用函数图象解不等式6x-4<3x+2
3、作出函数y=-2x-5的图象,观察图象回答下列问题:
① x取什么值时,-2x-5=0?
② x取什么值时,-2x-5>0?
③ x取什么值时,-2x-5≤0?
④ x取什么值时,-2x-5<34.兄弟俩赛跑,哥哥先让弟弟跑9米,然后自己才开始跑,已知弟弟每秒跑3米,哥哥每秒跑4米,设弟弟跑的时间为x秒,列出哥哥和弟弟跑的路程与x的函数关系式,作出函数图象,观察函数图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(2)谁先跑过20米?谁先跑过100米?5、拖拉机开始工作时,油箱中有油24L,那么油箱中剩余原油量y(L)与工作时间x(h)之间的函数关系式和图象是( )
A. y=4x-24(0≤x ≤ 6) B. y=24-4x
C. y=24-4x (0≤x ≤ 6 ) D. y=-24+4x ?
C例3. 如图,l1反映了某公司产品的销售收入与销售量的关系,(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;20003000 l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;60005000(3)当销售量为 时,销售收入等于销售成本;
销售成本是________元.4吨4000(4)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);大于4吨小于4吨如图,l1,l2分别为走私船和我公安快艇航行时路程与时间的函数图像.1)在刚出发时我公安快艇距走私船多少海里?2)计算走私船和公安快艇的速度分别是多少?3)写出l1,l2的解析式;4)问6分钟时两艇相距几海里;5)公安快艇能否追上走私船,若能几分钟追上?o4569l1l2ty/海里
点坐标是_____;当x>2时,y的取值
有何特点?x<2呢?函数与y轴的交
点坐标是_____;当y>-4时,x的取
值有何特点?y<-4呢?(2,0)(0,-4)看下面两个问题有什么关系:(1)解不等式5x+6>3x+10.
(2)当自变量x为何值时函数y=2x-4的值大于0?解(1) 2x-4>0
x>2解:(2)画图象2-4y=2x-40yx“解方程ax+b=0(a,b为常数)”与“求自变量x为何值时,一次函数y=ax+b的值为0”有什么关系?(同一个问题)问:(1)解不等式2x-4>0
(2)当自变量x为何值时函数y=2x-4的值大于0这两个问题有什么关系呢?因为函数值y>0,即2x-4>0
x>2(同一个问题)能否利用图象中观察不等式的解集呢?从图象上看,这相当于已知直线y=ax+b,确定它与x轴交点的横坐
标的值.画图象②观察x在什么范围时图象在x轴上方③(在x轴上方表明函数值y>0)所以此不等式的解集是x>2能否利用这个图象观察出2x-4<0的解集呢?(在x轴下方表明函数值y<0)所以此不等式2x-4<0的解集是x<2能否根据这个图象观察出不等式2x-4>2的解集呢?3“解方程ax+b=0(a,b为常数,a≠0)”与“求自变量x为何值时,一次函数y=ax+b的值为0”有什么关系?4“解不等式ax+b>0(a,b为常数,a≠0)”与“求自变量x为什么范围内,一次函数y=ax+b的值大于0”有什么关系?(同一个问题)由于任何一元一次不等式都可以转化为ax+b>0或ax<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数大(小)于0时,求自变量的相应的取值范围.探究归纳:
任何不等式都可以转化为ax+b>0或ax+b<0(a,ba≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大(小)于0时,求自变量相应的取值范围利用图象求不等式6x-3<x+2的解方法一:将方程变形为ax+b<0的形式5x-5<0转化为函数解析式画图象y=5x-5方法二:把不等式6x-3<x+2的两边看成是两个函数:即y1=6x-3,y2=x+2转化为两个函数画出两个函数图象找出交点(观察x在什么范围时图象y1点在y2点的下方)0-1yx1所以不等式6x-3<x+2的解是x<1所以不等式6x-3<x+2的解是x<1(观察x在什么范围时图象上的点是x轴下方)例2用画函数图像的方法解不等式5x+4<2x+10解法1:设y=3x-6并画出图像y-6x20解法1:设y1=5x+4;y2=2x+10并画出图像练习:
1、当自变量x的取值满足什么条件时,函数y=3x+8的值满足下列条件?
(1)y>0 (2)y<2
2、利用函数图象解不等式6x-4<3x+2
3、作出函数y=-2x-5的图象,观察图象回答下列问题:
① x取什么值时,-2x-5=0?
② x取什么值时,-2x-5>0?
③ x取什么值时,-2x-5≤0?
④ x取什么值时,-2x-5<34.兄弟俩赛跑,哥哥先让弟弟跑9米,然后自己才开始跑,已知弟弟每秒跑3米,哥哥每秒跑4米,设弟弟跑的时间为x秒,列出哥哥和弟弟跑的路程与x的函数关系式,作出函数图象,观察函数图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(2)谁先跑过20米?谁先跑过100米?5、拖拉机开始工作时,油箱中有油24L,那么油箱中剩余原油量y(L)与工作时间x(h)之间的函数关系式和图象是( )
A. y=4x-24(0≤x ≤ 6) B. y=24-4x
C. y=24-4x (0≤x ≤ 6 ) D. y=-24+4x ?
C例3. 如图,l1反映了某公司产品的销售收入与销售量的关系,(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;20003000 l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;60005000(3)当销售量为 时,销售收入等于销售成本;
销售成本是________元.4吨4000(4)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);大于4吨小于4吨如图,l1,l2分别为走私船和我公安快艇航行时路程与时间的函数图像.1)在刚出发时我公安快艇距走私船多少海里?2)计算走私船和公安快艇的速度分别是多少?3)写出l1,l2的解析式;4)问6分钟时两艇相距几海里;5)公安快艇能否追上走私船,若能几分钟追上?o4569l1l2ty/海里
