19.3课题学习选择方案
图片预览





文档简介
课件15张PPT。19.3 课题学习 选择方案第19章 一次函数练习题(1) 白炽灯功率60瓦,售价3元,每度电0.5 元/ (千瓦·时),使用1000小时的费用是多少元?
(2) 节能灯功率10瓦,售价60元,每度电0.5 元/(千瓦·时),使用1000小时的费用是多少元?
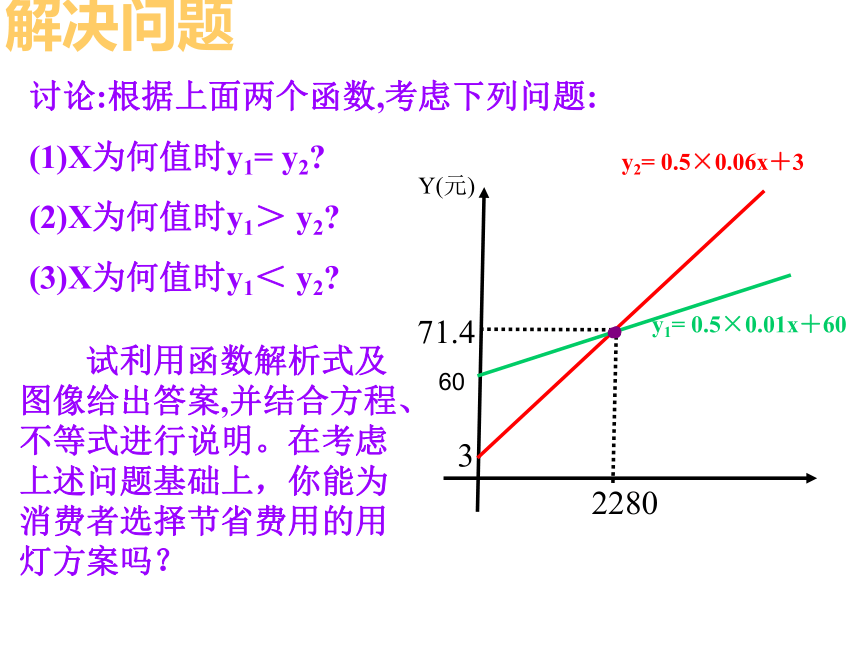
0.5×0.06×1000+3=33(元)0.5×0.01×1000+60=65(元) 你现在是小采购员,想在两种灯中选购一种,节能灯功率10瓦,售价为60元,白炽灯功率为60瓦,售价为3元,两种灯照明效果一样,使用寿命也相同(3000小时以上). 如果电费是0.5元/ (千瓦·时),选哪种灯可以节省费用?解决问题解:设照明时间为x小时,则节能灯的总费用y1为y1= 0.5×0.01x+60类似地可以写出白炽灯的总费用y2为y2= 0.5×0.06x+3解决问题讨论:根据上面两个函数,考虑下列问题:
(1)X为何值时y1= y2?
(2)X为何值时y1> y2?
(3)X为何值时y1< y2?
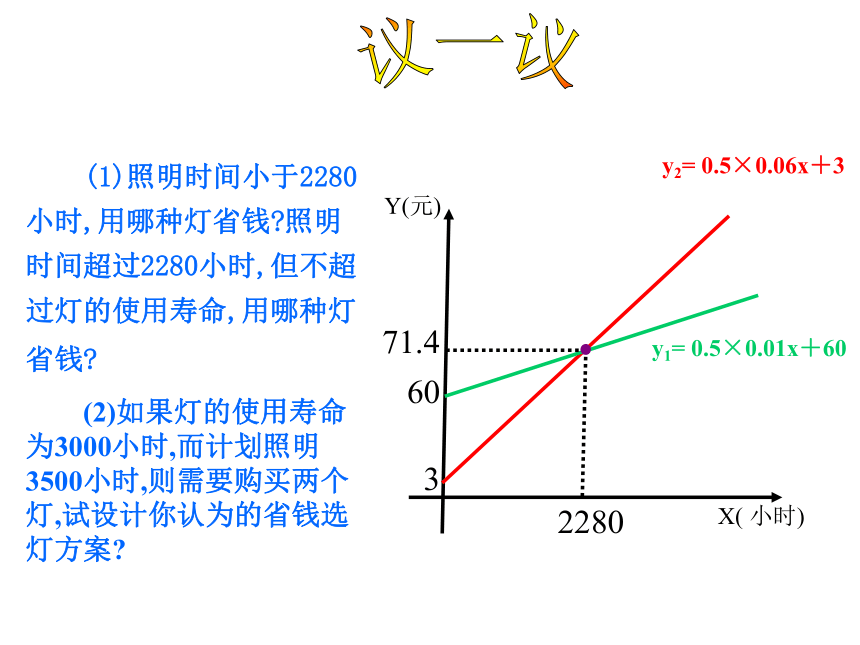
试利用函数解析式及图像给出答案,并结合方程、不等式进行说明。在考虑上述问题基础上,你能为消费者选择节省费用的用灯方案吗?Y(元)228071.4y2= 0.5×0.06x+3y1= 0.5×0.01x+60360议一议 (1)照明时间小于2280小时,用哪种灯省钱?照明时间超过2280小时,但不超过灯的使用寿命,用哪种灯省钱? (2)如果灯的使用寿命为3000小时,而计划照明3500小时,则需要购买两个灯,试设计你认为的省钱选灯方案?y1= 0.5×0.01x+60y2= 0.5×0.06x+3做一做 我校校长暑期带领学校市级“三好学生”去北京旅游,甲旅行社说:“如果校长买全票一张,则其余的学生可以享受半价优惠”.乙旅行社说:“包括校长全部按全票价的6折优惠”.已知全票价为240元.
(1)当学生人数是多少时,两家旅行社的收费一样? (2)若学生人数为9人时,哪家收费低? (3)若学生人数为3人时,哪家收费低? (4)你能否猜测出当学生人数在哪个范围时选用甲旅行社?
解决问题怎样租车 某学校计划在总费用2300元的限额内,利用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师。现有甲、乙两种大客车,它们的载客量和租金如表 :(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案。分析(1)要保证240名师生有车坐
(2)要使每辆汽车上至少要有1名教师根据(1)可知,汽车总数不能小于____;根据(2)可知,汽车总数不能大于____。综合起来可知汽车总数为 _____。 设租用x辆甲种客车,则租车费用y(单位:元)是 x 的函数,即 问题666y=400x+280(6-x)化简为: y=120x+1680讨论根据问题中的条件,自变量x 的取值应有几种可能? 为使240名师生有车坐,x不能 小于____;为使租车费用不超过2300元,X不能超过____。综合起来可知x 的取值为____ 。 在考虑上述问题的基础上,你能得出几种不同的租车方案?为节省费用应选择其中的哪种方案?试说明理由。问题464、54两甲种客车,2两乙种客车;5两甲种客车,1辆乙种客车;y1=120×4+1680=2160y2=120×5+1680=2280应选择方案一,它比方案二节约120元。方案一 解决问题怎样调水 从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨。从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米。设计一个调运方案使水的调运量(单位:万吨·千米)尽可能小。分析首先应考虑到影响水的调运量的因素有两个,即水量(单位:万吨)和运程(单位:千米),水的调运量是两者的乘积(单位:万吨·千米);其次应考虑到由A、B水库运往甲、乙两地的水量共4个量,即A--甲,A--乙,B--甲,B--乙的水量,它们互相联系。x15-x1514-xx-113141428设从A水库调往甲地的水量为x吨,则有:设水的运量为y万吨·千米,则有:y=50x+30(14-x)+60(15-x)+45(x-1)(1)y=5x+1275 1≤x≤14(3)最佳方案为:从A调往甲1万吨水, 调往乙13万吨水;从B调往甲14万吨水。
水的最小调运量为1280万吨·千米。(4)最佳方案相同。
(2) 节能灯功率10瓦,售价60元,每度电0.5 元/(千瓦·时),使用1000小时的费用是多少元?
0.5×0.06×1000+3=33(元)0.5×0.01×1000+60=65(元) 你现在是小采购员,想在两种灯中选购一种,节能灯功率10瓦,售价为60元,白炽灯功率为60瓦,售价为3元,两种灯照明效果一样,使用寿命也相同(3000小时以上). 如果电费是0.5元/ (千瓦·时),选哪种灯可以节省费用?解决问题解:设照明时间为x小时,则节能灯的总费用y1为y1= 0.5×0.01x+60类似地可以写出白炽灯的总费用y2为y2= 0.5×0.06x+3解决问题讨论:根据上面两个函数,考虑下列问题:
(1)X为何值时y1= y2?
(2)X为何值时y1> y2?
(3)X为何值时y1< y2?
试利用函数解析式及图像给出答案,并结合方程、不等式进行说明。在考虑上述问题基础上,你能为消费者选择节省费用的用灯方案吗?Y(元)228071.4y2= 0.5×0.06x+3y1= 0.5×0.01x+60360议一议 (1)照明时间小于2280小时,用哪种灯省钱?照明时间超过2280小时,但不超过灯的使用寿命,用哪种灯省钱? (2)如果灯的使用寿命为3000小时,而计划照明3500小时,则需要购买两个灯,试设计你认为的省钱选灯方案?y1= 0.5×0.01x+60y2= 0.5×0.06x+3做一做 我校校长暑期带领学校市级“三好学生”去北京旅游,甲旅行社说:“如果校长买全票一张,则其余的学生可以享受半价优惠”.乙旅行社说:“包括校长全部按全票价的6折优惠”.已知全票价为240元.
(1)当学生人数是多少时,两家旅行社的收费一样? (2)若学生人数为9人时,哪家收费低? (3)若学生人数为3人时,哪家收费低? (4)你能否猜测出当学生人数在哪个范围时选用甲旅行社?
解决问题怎样租车 某学校计划在总费用2300元的限额内,利用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师。现有甲、乙两种大客车,它们的载客量和租金如表 :(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案。分析(1)要保证240名师生有车坐
(2)要使每辆汽车上至少要有1名教师根据(1)可知,汽车总数不能小于____;根据(2)可知,汽车总数不能大于____。综合起来可知汽车总数为 _____。 设租用x辆甲种客车,则租车费用y(单位:元)是 x 的函数,即 问题666y=400x+280(6-x)化简为: y=120x+1680讨论根据问题中的条件,自变量x 的取值应有几种可能? 为使240名师生有车坐,x不能 小于____;为使租车费用不超过2300元,X不能超过____。综合起来可知x 的取值为____ 。 在考虑上述问题的基础上,你能得出几种不同的租车方案?为节省费用应选择其中的哪种方案?试说明理由。问题464、54两甲种客车,2两乙种客车;5两甲种客车,1辆乙种客车;y1=120×4+1680=2160y2=120×5+1680=2280应选择方案一,它比方案二节约120元。方案一 解决问题怎样调水 从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨。从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米。设计一个调运方案使水的调运量(单位:万吨·千米)尽可能小。分析首先应考虑到影响水的调运量的因素有两个,即水量(单位:万吨)和运程(单位:千米),水的调运量是两者的乘积(单位:万吨·千米);其次应考虑到由A、B水库运往甲、乙两地的水量共4个量,即A--甲,A--乙,B--甲,B--乙的水量,它们互相联系。x15-x1514-xx-113141428设从A水库调往甲地的水量为x吨,则有:设水的运量为y万吨·千米,则有:y=50x+30(14-x)+60(15-x)+45(x-1)(1)y=5x+1275 1≤x≤14(3)最佳方案为:从A调往甲1万吨水, 调往乙13万吨水;从B调往甲14万吨水。
水的最小调运量为1280万吨·千米。(4)最佳方案相同。
