19.2.2一次函数的图像与性质 课件
文档属性
| 名称 | 19.2.2一次函数的图像与性质 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-15 11:04:23 | ||
图片预览






文档简介
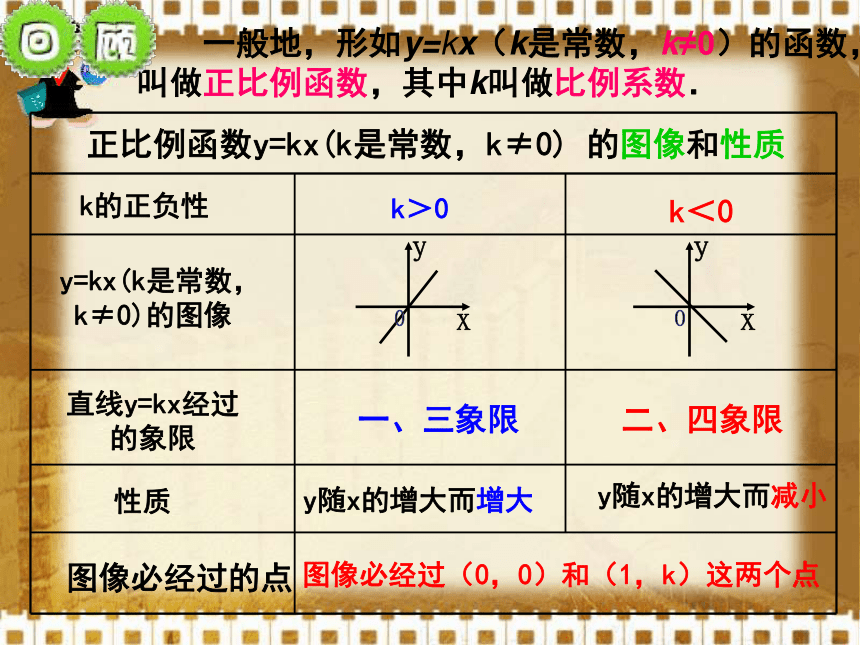
课件47张PPT。提问复习1、什么叫正比例函数、一次函数?它们之间有什么关系?2、正比例函数的图象是什么形状? 把形如y=kx(k是常数,k≠0) 的函数,叫做正比例函数; 把形如y=kx+b(k,b是常数,k≠0) 的函数,叫做一次函数。 当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。正比例函数的图象是( )y=kx经过原点的一条直线k>0k<0一、三象限二、四象限y随x的增大而减小y随x的增大而增大图像必经过(0,0)和(1,k)这两个点 一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数. 既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么,
1、一次函数的图象也会是一条直线吗?
2、它们图象之间有什么关系?
3、一次函数又有什么性质呢?创设问题19.2.2一次函数
第2课时
一次函数的图像与性质
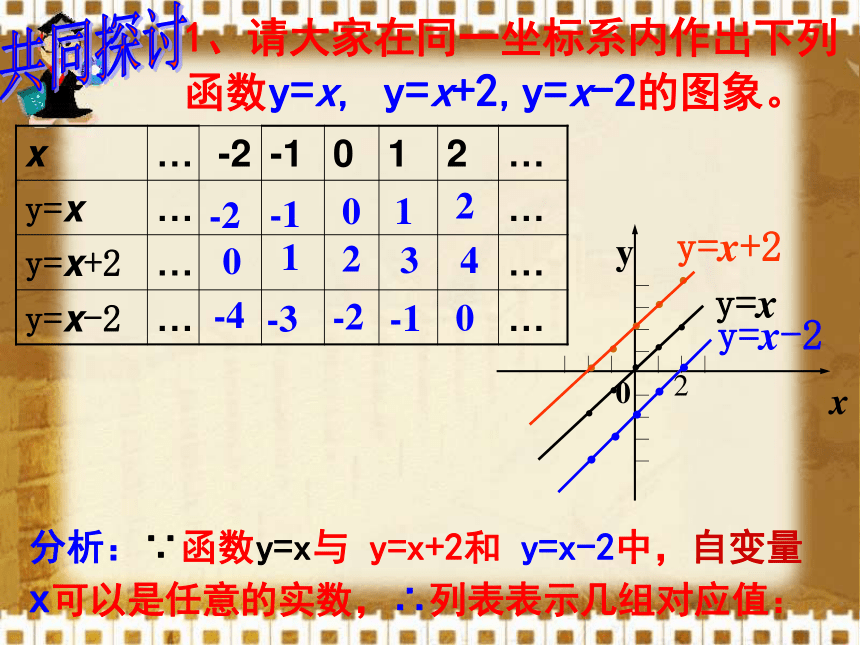
.......1、请大家在同一坐标系内作出下列函数y=x, y=x+2,y=x-2的图象。-20-3-11-402-213-1240....y=x....y=x+2y=x-2分析:∵函数y=x与 y=x+2和 y=x-2中,自变量x可以是任意的实数,∴列表表示几组对应值:共同探讨2、观察与比较:正比例函数y=x与一次函数y=x+2 、y=x-2图象有什么异同点.
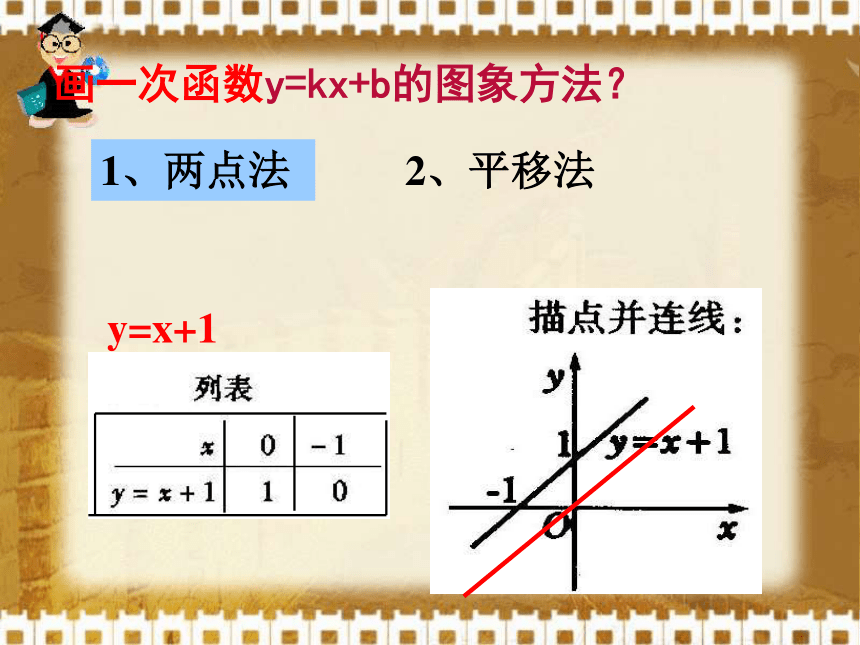
归纳:这几个函数的图象形状都是 ,并且倾斜程度____函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____ 个单位长度而得到.直线相同(0,2)上2(0,-2)下22画一次函数y=kx+b的图象方法?1、两点法 y=x+12、平移法y=xy=x+2y=x-2y30 一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到。(当b>0时,向上平移;当b<0时,向下平移)实验探讨:
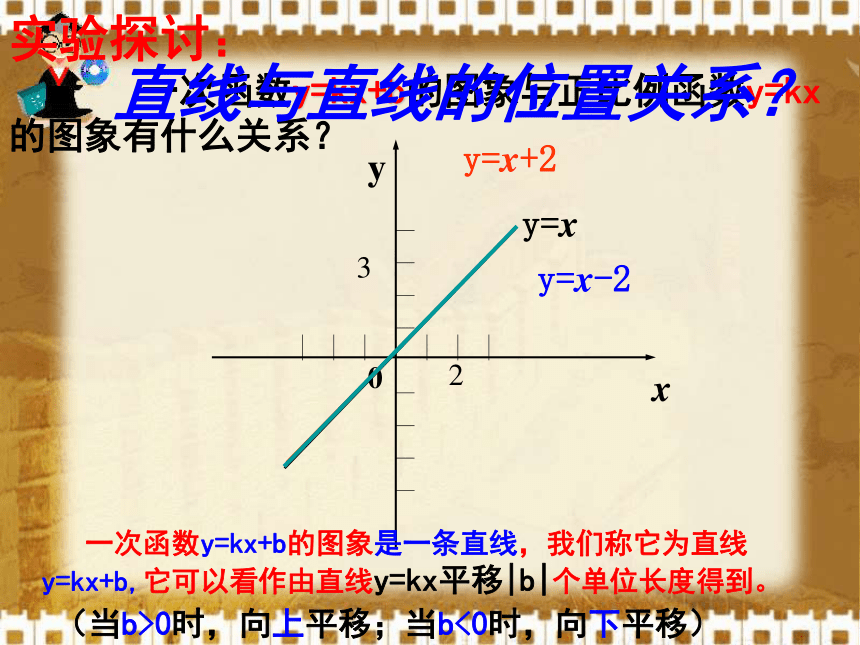
一次函数y=kx+b的图象与正比例函数y=kx的图象有什么关系?直线与直线的位置关系?(1) 所有一次函数y=kx+b的图象都是________(2)直线 y=kx+b与直线y=kx__________;(3)直线 y=kx+b可以看作由直线y=kx___________
而得到一条直线;互相平行平移 个单位当b>0,向上平移b个单位;
当b<0,向下平移b个单位。探讨总结 1直线y=k1x+b1与y=k2x+b2的位置关系
(1)两直线平行:k1=k2且b1≠ b2
(2)两直线相交:k1 ≠ k2
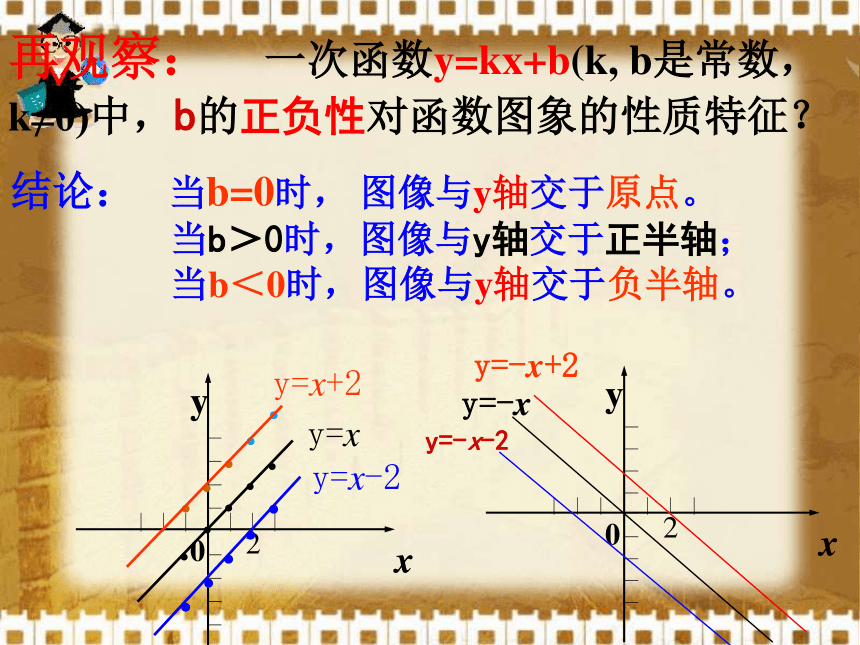
(3)两直线重合:k1=k2且b1=b2再观察: 一次函数y=kx+b(k, b是常数,k≠0)中,b的正负性对函数图象的性质特征?结论: 当b=0时, 图像与y轴交于原点。
当b>0时,图像与y轴交于正半轴;
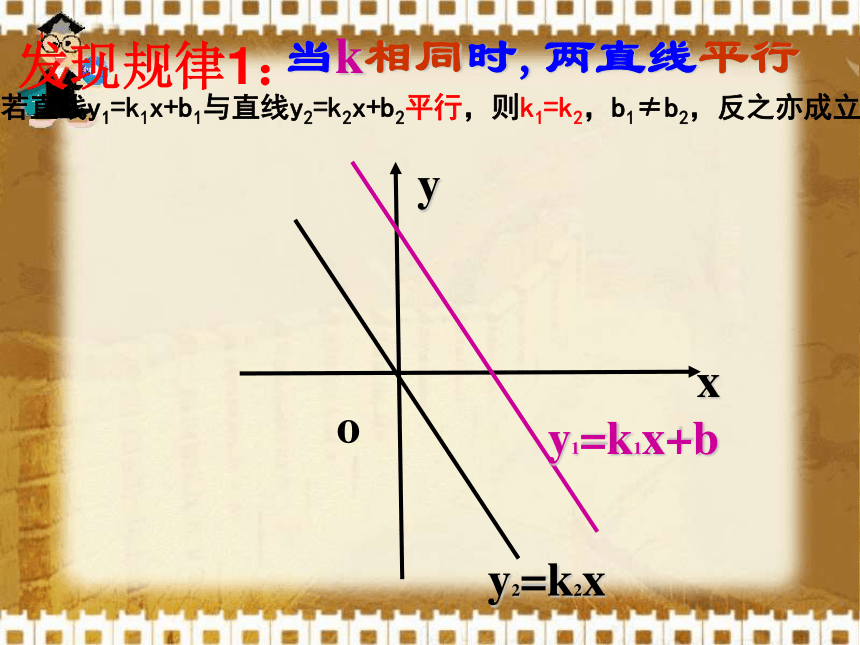
当b<0时,图像与y轴交于负半轴。y=-xy=-x+2y=-x-2oy2=k2xy1=k1x+bxy当k相同时,两直线平行发现规律1:若直线y1=k1x+b1与直线y2=k2x+b2平行,则k1=k2,b1≠b2,反之亦成立。
已知直线y=kx+5与直线y=3x-7平行,则k= .变式一:已知直线y=(3k-5)x+7与直线y=-2x+9平行,则k= .变式二:已知直线y=(a+3)x-5与直线y=(15-2a)x+4平行,则a= .3解:∵3k-5=-2, ∴3k=3,即k=11解: ∵a+3=15-2a,
∴3a=12,即a=4.4脑力奔腾,检测效果例1. 画出函数y=2x-1的图象 如何画出一次函数y=kx+b的图象?y=2x -1解:画一次函数的图象最少需要几个点? 分析:由于一次函数的图象是直线,所以只要确定两个合适的点就能画出它。共同探讨2例2. 画出函数y=-0.5x -1的图象y=-0.5x -1 一次函数y=kx+b(k≠0)的图象与两坐标轴的交点的坐标:取x=0,则得y=b,∴得与y轴的交点坐标为(0,b);
取y=0,则得x=-b/k,∴得与x轴的交点坐标为(-b/k,0)通常选取点(0,b),(-b/k,o)这两点。b决定直线与y轴相交时的交点的位置。K决定直线倾斜的方向。规律发现: 用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.0
0
-1
0
0.5012经过(0,-1)和(0.5,0)两点经过(0,1)和(2,0)两点y=2x-1y=-0.5x+1实践巩固:1、正比例函数的图象是什么? 如何画出正比例函数的图象?(直线)(描两点并画出直线)2、一次函数的图象是什么? 如何画出一次函数的图象?(直线)(描两点并画出直线)(0,0)(1,k)(0,b)
( ,0)(0 ,b)(1 , k+b) 或 以确定特殊自变量0、1来定两点以坐标轴上坐标特点来确定两点你总结并回答这两个点,也就是选取图像与x轴和y轴的交点坐标。
继续探究3 一次函数y=kx+b(k,b是常数,k≠0)中,k的正负性对函数图象的性质特征? 在同直角一坐标系中,画出函数(1) y=x+1, y=x-1, (2) y=-2x-1, y=-2x+l 的图象.上升增大>发现规律2:当k>0时,y随x的增大而增大;一次函数的增减性?1.比较函数图象,直线y=-2x+1和y=-2x-1由左向右 ,y随x的增大而 。
2.比较函数解析式,直线y=-2x+1和y=-2x-1中k 0。继续探究3减小下降<同样,我们可以画出函数 y=-2x+l, y=-2x-1的图象发现规律3:当k<0时,y随x的增大而减小 。一次函数的增减性?一次函数的增减性与b值无关.一次函数 y=kx+b k 决定直线的倾斜程度和方向当k>0时,y随x的增大而增大2.当k<0时,y随x的增大而减少3.当 k 相等时,直线平行4.当 |k| 越大时,图象越靠近y轴一次函数 y=kx+b b 决定直线与y轴交点位置当b>0时,直线交于y正半轴4.当 k 相等时,直线交于y轴上同一点2.当b<0时,直线交于y负半轴3.当b = 0时,直线交于坐标原点正比例函数正比例函数一次函数y=kx+b(k、b是常数,k≠0) 的图像和性质k的正负性k>0k<0b取正、负、0性质画图常用
的两个点b>0b<0b=0b>0b=0b<0示意图图像经过的
象限一、二、三
象限一、三
象限一、三、四
象限一、二、四
象限二、四
象限二、三、四
象限y随x的增大而减小y随x的增大而增大(0,0)
(1,k)(0,b)
(1,k+b)(0,b)
(1,k+b)(0,b)
(1,k+b)(0,b)
(1,k+b)(0,0)
(1,k)(-b/k,0)(-b/k,0)(-b/k,0)(-b/k,0)一次函数图像经过象限的速记方法:K正画/,左低右高,b正交y轴正半轴,b负交y轴负半轴。
K负画,左高右低,b正交y轴正半轴,b负交y轴负半轴。知识总结根据函数图象确定k,b的取值范围yxoK>o, b=oyxoK>0, bo, b>0yxoK<0, b=0yx0K<0, b<0yxoK<0, b>0小试牛刀小结告诉大家本节课你的收获!3.会用:一次函数的性质1.会画:用两点法画一次函数的图象2.会求:一次函数与坐标轴的交点以刻苦学习为荣以放弃学习为耻 课 堂 总 结
形如y=kx+b(k,b是常数,k≠0),称y是做x的一次函数.
(1)解析式:y=kx+b(k、b是常数,k ≠ 0)
(2)必过点:(0,b)和( - ,0)
(3)走向:k>0 b>0直线经过第一、二、三象限
k>0 b<0直线经过第一、三、四象限
K<0 b>0直线经过第一、二、四象限
K<0 b>0直线经过第二、三、四象限
(4)增减性: k>0,y随x的增大而增大;
k<0,y随x增大而减小.
(5)倾斜度:|k|越大,图象越接近于y轴;
|k|越小,图象越接近于x轴.
(6)图像的平移:
当b>0时,将直线y=kx的图象向上平移b个单位;
当b<0时,将直线y=kx的图象向下平移b个单位.1.函数y=10x-9的图象经过第_________象限,y的值随着x值的增大而________.
2.函数y=-0.3x+4的图象经过第____________象限,y的值随着x值的增大而 __________.
3.直线y=-x-2的图象不经过第________象限.
4.直线y=k(x-k) (k>0)的图象经过第________ 象限增大减小y=kx-k2一一、三、四一 、三、 四一、 二、 四课堂检测:(1)下列函数中,y的值随x值的增大而增大的函数是________. A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2C(2)直线y=3x-2可由直线y=3x向 平移 单位得到。(3)直线y=x+2可由直线y=x-1向 平移 单位得到。下2上3课堂检测:(4)对于函数y=5x+6,y的值随x的值减小而______。(5)函数y=2x-1经过 象限减少一、三、四(6)函数y=2x - 4与y轴的交点为 ( ),与x轴交于( )0,-42, 0课堂检测: 已知:一次函数 y=(5m-3)x+(2-n).
(1)当 m 为何值时,y 随 x 的增大而减小;
(2)当 m、n 分别为何值时,一次函数与 y 轴 的交点在 x 轴的上方?课堂检测:例 题例2、对于一次函数y=(a+4)x+2a-1,如果y随x的增大而增大,且它的图象与y轴的交点在x轴的下方,试求a的取值范围解:因为 y随x的增大而增大,
所以 a+4>0 即 a>-4又因为它的图象与y轴的交点在x轴的下方
所以 2a-1 < 0 即 a < 1/2所以 -4 < a < 1/2(2013?安溪)已知实数a、b满足ab>0,a+b<0,则一次函数y=ax-b的图象可能是( )
考点:一次函数图象与系数的关系.
专题:数形结合.
分析:根据实数的性质得到a<0,b<0,然后根据一次函数图象与系数的关系进行判断.
解答
∵实数a、b满足ab>0,a+b<0,
∴a<0,b<0,
∴-b>0,
∴一次函数y=ax-b的图象经过第一、二、四象限.
故选B.
点评:本题考查了一次函数图象与系数的关系:一次函数y=kx+b(k、b为常数,k≠0)的图象为直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;直线与y轴的交点坐标为(0,b).(2012陕西)在下列四组点中,可以在同一个正比例函数图象上的一组点是( )
A. (2,﹣3),(﹣4,6) B. (﹣2,3),(4,6)
C. (﹣2,﹣3),(4,﹣6) D. (2,3),(﹣4,6)考点:一次函数图象上点的坐标特征分析:由于正比例函数图象上点的纵坐标和横坐标的比相同,找到比值相同的一组数即可. A【解析】本题考查了一次函数的图象性质以及应用,若干点在同一个正比例函数图像上,
由正比例函数y=kx
可知,y与x的比值是相等的,代进去求解,可知,A为正确解.选A.练习一1.下列函数中,不是一次函数的是 ( )
2.如图,正比例函数图像经过点A,该函数解析式是______4.点P(a,b)点Q(c,d)是一次函数y=-4x+3图像上的两个点,且ad1.一次函数 y 1=kx+b与y 2=x+a的图像如图所示,则下列结论(1)k<0;(2)a>0;(3)当x<3时,y 1 ∴k=-2∵图像经过点(0,4)
∴b=4∴此函数的解析式为y= - 2x+4∵函数y= - 2x+4与两坐标轴的交点为(0,4) (2,0)∴S△= ×2 ×4=4练 习 直线y=kx+b与y轴相交于点(0, b), b叫做直线y=kx+b在y轴上的截距,简称截距注意:截距b不是距离,它可以是正数,也可以是负数或零.(0, b)0 图象与y轴交于(0,b) ,b就是与y轴交点的纵坐标,正在原点上方,负在原点下方。
k叫直线y=kx+b的斜率 一次函数y=kx+b的图象是经过(0,b)的点且平行于直线y=kx的一条直线.4.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,
…按如图所示的方式放置.点A1,A2,A3,
…和点C1,C2,C3,…分别在直线y=kx+b
(k>0)和x轴上,已知点B1(1,1),
B2(3,2),则Bn的坐标是_________. 1、直线y=2x+1与y=3x-1的交点P的坐标为____,点P到x轴的距离为_______,点P到y轴的距离为______。2.一次函数的图象过点(0,3) ,且与两坐标轴围成的三角形面积为 9/4,一次函数的解析式为_________________。3.如图,将直线OA向上平移1个单位,
得到一个一次函数的图像,那么这个一次
函数的解析式是____________________y=2x+12 5y=±2x+3(2, 5)反馈练习三(2012?乐山)若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是( )
考点:一次函数图象与系数的关系.
分析:先判断出a是负数,c是正数,然后根据一次函数图象与系数的关系确定图象经过的象限以及与y轴的交点的位置即可得解.
解答
∵a+b+c=0,且a<b<c,
∴a<0,c>0,(b的正负情况不能确定),
a<0,则函数y=ax+c图象经过第二四象限,
c>0,则函数y=ax+c的图象与y轴正半轴相交,
纵观各选项,只有A选项符合.
故选A. 一次函数图象和性质第一、三象限y随x增大
而增大 第一、二、三象限y随x增大
而增大第一、三、四象限y随x的增大
而增大(0, b)(0, b)先由k决定过一三象限,
再由b决定过二或四象限由k决定第二、四象限y随x增大
而减小第一、二、四象限y随x增大
而减小第二、三、四象限y随x增大
而减小(0, b)(o, b)先由k决定过二四象限,
再由b决定过一或三象限由k决定 、一次函数图象与性质y随x的增
大而增大y随x的增
大而增大y随x的增
大而减少y随x的增
大而减少一、二、三一、三、四一、二、四二、三、四k>0
b>0k>0
b<0k<0
b>0k<0
b<0一次函数y=kx+b (k?0)的性质:
当k>0时,y随x的增大而增大;
yx一次函数y=kx+b (k?0)的性质:当k<0时,y随x的增大而减小.yx已知一次函数y=2x-4.⑴求它与两坐标轴的交点坐标.⑵求它与两坐标轴围成的三角形的面积.变形1:已知一次函数y=2x+b的图象与两坐标轴围成的三角形的面积为4.求b的值.变形2:已知一次函数y=kx+4的图象与两坐标轴围成的三角形的面积为4.求k的值.4.与面积有关的问题变形3:已知一次函数y=2x-4和一次函数 y=-x+4.
(1)求两图象的交点坐标 ;
(2)求两图象与y轴围成的三角形的面积.
(3) 求两图象与坐标轴围成的图形的面积.ACBDy=-x+4y=2x-4(-4,0)(0,4)(4,0)(2,0)E14.(1) 在同一直角坐标系中,画出直线y=x+3与 y=-2x+3;
(2)设(1)中两个图象交于点P,且它们与x轴分别交于点A,B.求△PAB的面积.ABADy=-2x+3y=x+3(-3,0)(3,0)(1.5,0)(3,4)P
1、一次函数的图象也会是一条直线吗?
2、它们图象之间有什么关系?
3、一次函数又有什么性质呢?创设问题19.2.2一次函数
第2课时
一次函数的图像与性质
.......1、请大家在同一坐标系内作出下列函数y=x, y=x+2,y=x-2的图象。-20-3-11-402-213-1240....y=x....y=x+2y=x-2分析:∵函数y=x与 y=x+2和 y=x-2中,自变量x可以是任意的实数,∴列表表示几组对应值:共同探讨2、观察与比较:正比例函数y=x与一次函数y=x+2 、y=x-2图象有什么异同点.
归纳:这几个函数的图象形状都是 ,并且倾斜程度____函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____ 个单位长度而得到.直线相同(0,2)上2(0,-2)下22画一次函数y=kx+b的图象方法?1、两点法 y=x+12、平移法y=xy=x+2y=x-2y30 一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到。(当b>0时,向上平移;当b<0时,向下平移)实验探讨:
一次函数y=kx+b的图象与正比例函数y=kx的图象有什么关系?直线与直线的位置关系?(1) 所有一次函数y=kx+b的图象都是________(2)直线 y=kx+b与直线y=kx__________;(3)直线 y=kx+b可以看作由直线y=kx___________
而得到一条直线;互相平行平移 个单位当b>0,向上平移b个单位;
当b<0,向下平移b个单位。探讨总结 1直线y=k1x+b1与y=k2x+b2的位置关系
(1)两直线平行:k1=k2且b1≠ b2
(2)两直线相交:k1 ≠ k2
(3)两直线重合:k1=k2且b1=b2再观察: 一次函数y=kx+b(k, b是常数,k≠0)中,b的正负性对函数图象的性质特征?结论: 当b=0时, 图像与y轴交于原点。
当b>0时,图像与y轴交于正半轴;
当b<0时,图像与y轴交于负半轴。y=-xy=-x+2y=-x-2oy2=k2xy1=k1x+bxy当k相同时,两直线平行发现规律1:若直线y1=k1x+b1与直线y2=k2x+b2平行,则k1=k2,b1≠b2,反之亦成立。
已知直线y=kx+5与直线y=3x-7平行,则k= .变式一:已知直线y=(3k-5)x+7与直线y=-2x+9平行,则k= .变式二:已知直线y=(a+3)x-5与直线y=(15-2a)x+4平行,则a= .3解:∵3k-5=-2, ∴3k=3,即k=11解: ∵a+3=15-2a,
∴3a=12,即a=4.4脑力奔腾,检测效果例1. 画出函数y=2x-1的图象 如何画出一次函数y=kx+b的图象?y=2x -1解:画一次函数的图象最少需要几个点? 分析:由于一次函数的图象是直线,所以只要确定两个合适的点就能画出它。共同探讨2例2. 画出函数y=-0.5x -1的图象y=-0.5x -1 一次函数y=kx+b(k≠0)的图象与两坐标轴的交点的坐标:取x=0,则得y=b,∴得与y轴的交点坐标为(0,b);
取y=0,则得x=-b/k,∴得与x轴的交点坐标为(-b/k,0)通常选取点(0,b),(-b/k,o)这两点。b决定直线与y轴相交时的交点的位置。K决定直线倾斜的方向。规律发现: 用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.0
0
-1
0
0.5012经过(0,-1)和(0.5,0)两点经过(0,1)和(2,0)两点y=2x-1y=-0.5x+1实践巩固:1、正比例函数的图象是什么? 如何画出正比例函数的图象?(直线)(描两点并画出直线)2、一次函数的图象是什么? 如何画出一次函数的图象?(直线)(描两点并画出直线)(0,0)(1,k)(0,b)
( ,0)(0 ,b)(1 , k+b) 或 以确定特殊自变量0、1来定两点以坐标轴上坐标特点来确定两点你总结并回答这两个点,也就是选取图像与x轴和y轴的交点坐标。
继续探究3 一次函数y=kx+b(k,b是常数,k≠0)中,k的正负性对函数图象的性质特征? 在同直角一坐标系中,画出函数(1) y=x+1, y=x-1, (2) y=-2x-1, y=-2x+l 的图象.上升增大>发现规律2:当k>0时,y随x的增大而增大;一次函数的增减性?1.比较函数图象,直线y=-2x+1和y=-2x-1由左向右 ,y随x的增大而 。
2.比较函数解析式,直线y=-2x+1和y=-2x-1中k 0。继续探究3减小下降<同样,我们可以画出函数 y=-2x+l, y=-2x-1的图象发现规律3:当k<0时,y随x的增大而减小 。一次函数的增减性?一次函数的增减性与b值无关.一次函数 y=kx+b k 决定直线的倾斜程度和方向当k>0时,y随x的增大而增大2.当k<0时,y随x的增大而减少3.当 k 相等时,直线平行4.当 |k| 越大时,图象越靠近y轴一次函数 y=kx+b b 决定直线与y轴交点位置当b>0时,直线交于y正半轴4.当 k 相等时,直线交于y轴上同一点2.当b<0时,直线交于y负半轴3.当b = 0时,直线交于坐标原点正比例函数正比例函数一次函数y=kx+b(k、b是常数,k≠0) 的图像和性质k的正负性k>0k<0b取正、负、0性质画图常用
的两个点b>0b<0b=0b>0b=0b<0示意图图像经过的
象限一、二、三
象限一、三
象限一、三、四
象限一、二、四
象限二、四
象限二、三、四
象限y随x的增大而减小y随x的增大而增大(0,0)
(1,k)(0,b)
(1,k+b)(0,b)
(1,k+b)(0,b)
(1,k+b)(0,b)
(1,k+b)(0,0)
(1,k)(-b/k,0)(-b/k,0)(-b/k,0)(-b/k,0)一次函数图像经过象限的速记方法:K正画/,左低右高,b正交y轴正半轴,b负交y轴负半轴。
K负画,左高右低,b正交y轴正半轴,b负交y轴负半轴。知识总结根据函数图象确定k,b的取值范围yxoK>o, b=oyxoK>0, b
形如y=kx+b(k,b是常数,k≠0),称y是做x的一次函数.
(1)解析式:y=kx+b(k、b是常数,k ≠ 0)
(2)必过点:(0,b)和( - ,0)
(3)走向:k>0 b>0直线经过第一、二、三象限
k>0 b<0直线经过第一、三、四象限
K<0 b>0直线经过第一、二、四象限
K<0 b>0直线经过第二、三、四象限
(4)增减性: k>0,y随x的增大而增大;
k<0,y随x增大而减小.
(5)倾斜度:|k|越大,图象越接近于y轴;
|k|越小,图象越接近于x轴.
(6)图像的平移:
当b>0时,将直线y=kx的图象向上平移b个单位;
当b<0时,将直线y=kx的图象向下平移b个单位.1.函数y=10x-9的图象经过第_________象限,y的值随着x值的增大而________.
2.函数y=-0.3x+4的图象经过第____________象限,y的值随着x值的增大而 __________.
3.直线y=-x-2的图象不经过第________象限.
4.直线y=k(x-k) (k>0)的图象经过第________ 象限增大减小y=kx-k2一一、三、四一 、三、 四一、 二、 四课堂检测:(1)下列函数中,y的值随x值的增大而增大的函数是________. A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2C(2)直线y=3x-2可由直线y=3x向 平移 单位得到。(3)直线y=x+2可由直线y=x-1向 平移 单位得到。下2上3课堂检测:(4)对于函数y=5x+6,y的值随x的值减小而______。(5)函数y=2x-1经过 象限减少一、三、四(6)函数y=2x - 4与y轴的交点为 ( ),与x轴交于( )0,-42, 0课堂检测: 已知:一次函数 y=(5m-3)x+(2-n).
(1)当 m 为何值时,y 随 x 的增大而减小;
(2)当 m、n 分别为何值时,一次函数与 y 轴 的交点在 x 轴的上方?课堂检测:例 题例2、对于一次函数y=(a+4)x+2a-1,如果y随x的增大而增大,且它的图象与y轴的交点在x轴的下方,试求a的取值范围解:因为 y随x的增大而增大,
所以 a+4>0 即 a>-4又因为它的图象与y轴的交点在x轴的下方
所以 2a-1 < 0 即 a < 1/2所以 -4 < a < 1/2(2013?安溪)已知实数a、b满足ab>0,a+b<0,则一次函数y=ax-b的图象可能是( )
考点:一次函数图象与系数的关系.
专题:数形结合.
分析:根据实数的性质得到a<0,b<0,然后根据一次函数图象与系数的关系进行判断.
解答
∵实数a、b满足ab>0,a+b<0,
∴a<0,b<0,
∴-b>0,
∴一次函数y=ax-b的图象经过第一、二、四象限.
故选B.
点评:本题考查了一次函数图象与系数的关系:一次函数y=kx+b(k、b为常数,k≠0)的图象为直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;直线与y轴的交点坐标为(0,b).(2012陕西)在下列四组点中,可以在同一个正比例函数图象上的一组点是( )
A. (2,﹣3),(﹣4,6) B. (﹣2,3),(4,6)
C. (﹣2,﹣3),(4,﹣6) D. (2,3),(﹣4,6)考点:一次函数图象上点的坐标特征分析:由于正比例函数图象上点的纵坐标和横坐标的比相同,找到比值相同的一组数即可. A【解析】本题考查了一次函数的图象性质以及应用,若干点在同一个正比例函数图像上,
由正比例函数y=kx
可知,y与x的比值是相等的,代进去求解,可知,A为正确解.选A.练习一1.下列函数中,不是一次函数的是 ( )
2.如图,正比例函数图像经过点A,该函数解析式是______4.点P(a,b)点Q(c,d)是一次函数y=-4x+3图像上的两个点,且a
∴b=4∴此函数的解析式为y= - 2x+4∵函数y= - 2x+4与两坐标轴的交点为(0,4) (2,0)∴S△= ×2 ×4=4练 习 直线y=kx+b与y轴相交于点(0, b), b叫做直线y=kx+b在y轴上的截距,简称截距注意:截距b不是距离,它可以是正数,也可以是负数或零.(0, b)0 图象与y轴交于(0,b) ,b就是与y轴交点的纵坐标,正在原点上方,负在原点下方。
k叫直线y=kx+b的斜率 一次函数y=kx+b的图象是经过(0,b)的点且平行于直线y=kx的一条直线.4.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,
…按如图所示的方式放置.点A1,A2,A3,
…和点C1,C2,C3,…分别在直线y=kx+b
(k>0)和x轴上,已知点B1(1,1),
B2(3,2),则Bn的坐标是_________. 1、直线y=2x+1与y=3x-1的交点P的坐标为____,点P到x轴的距离为_______,点P到y轴的距离为______。2.一次函数的图象过点(0,3) ,且与两坐标轴围成的三角形面积为 9/4,一次函数的解析式为_________________。3.如图,将直线OA向上平移1个单位,
得到一个一次函数的图像,那么这个一次
函数的解析式是____________________y=2x+12 5y=±2x+3(2, 5)反馈练习三(2012?乐山)若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是( )
考点:一次函数图象与系数的关系.
分析:先判断出a是负数,c是正数,然后根据一次函数图象与系数的关系确定图象经过的象限以及与y轴的交点的位置即可得解.
解答
∵a+b+c=0,且a<b<c,
∴a<0,c>0,(b的正负情况不能确定),
a<0,则函数y=ax+c图象经过第二四象限,
c>0,则函数y=ax+c的图象与y轴正半轴相交,
纵观各选项,只有A选项符合.
故选A. 一次函数图象和性质第一、三象限y随x增大
而增大 第一、二、三象限y随x增大
而增大第一、三、四象限y随x的增大
而增大(0, b)(0, b)先由k决定过一三象限,
再由b决定过二或四象限由k决定第二、四象限y随x增大
而减小第一、二、四象限y随x增大
而减小第二、三、四象限y随x增大
而减小(0, b)(o, b)先由k决定过二四象限,
再由b决定过一或三象限由k决定 、一次函数图象与性质y随x的增
大而增大y随x的增
大而增大y随x的增
大而减少y随x的增
大而减少一、二、三一、三、四一、二、四二、三、四k>0
b>0k>0
b<0k<0
b>0k<0
b<0一次函数y=kx+b (k?0)的性质:
当k>0时,y随x的增大而增大;
yx一次函数y=kx+b (k?0)的性质:当k<0时,y随x的增大而减小.yx已知一次函数y=2x-4.⑴求它与两坐标轴的交点坐标.⑵求它与两坐标轴围成的三角形的面积.变形1:已知一次函数y=2x+b的图象与两坐标轴围成的三角形的面积为4.求b的值.变形2:已知一次函数y=kx+4的图象与两坐标轴围成的三角形的面积为4.求k的值.4.与面积有关的问题变形3:已知一次函数y=2x-4和一次函数 y=-x+4.
(1)求两图象的交点坐标 ;
(2)求两图象与y轴围成的三角形的面积.
(3) 求两图象与坐标轴围成的图形的面积.ACBDy=-x+4y=2x-4(-4,0)(0,4)(4,0)(2,0)E14.(1) 在同一直角坐标系中,画出直线y=x+3与 y=-2x+3;
(2)设(1)中两个图象交于点P,且它们与x轴分别交于点A,B.求△PAB的面积.ABADy=-2x+3y=x+3(-3,0)(3,0)(1.5,0)(3,4)P
