第六章计数原理 单元测评-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册(含答案)
文档属性
| 名称 | 第六章计数原理 单元测评-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 264.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 12:58:32 | ||
图片预览


文档简介
魏县第五中学高二数学第六章测评一、单选题(每小题5分,共40分)
1.的展开式中的常数项为
A. B. C. D.
2.小林同学喜欢吃4种坚果:核桃 腰果 杏仁 榛子,他有5种颜色的“每日坚果”袋.每个袋子中至少装1种坚果,至多装4种坚果.小林同学希望五个袋子中所装坚果种类各不相同,且每一种坚果在袋子中出现的总次数均为偶数,那么不同的方案数为( )
A.20160 B.20220 C.20280 D.20340
3.如果的展开式中含有常数项,则正整数n的最小值是( )
A.3 B.4 C.5 D.6
4.若,则( )
A.27 B.-27 C.54 D.-54
5.现有十二生肖的吉祥物各一个,已知甲同学喜欢牛、马和猴的吉祥物,乙同学喜欢牛、狗和羊的吉祥物,丙同学对所有的吉祥物都喜欢,让甲、乙、丙三位同学依次从中选一个珍藏,若每个人所选取的礼物都是自己喜欢的,则不同的选法共有( )
A.50种 B.60种 C.80种 D.90种
6.名同学报名参加个活动小组,每人限报个活动小组,不同的报名方法种数为( )
A. B. C. D.
7.若的展开式中各项的二项式系数之和为512,且第6项的系数最大,则a的取值范围为( )
A. B.
C. D.
8.5名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排2名,则不同的安排方法共有( )
A.120种 B.90种 C.60种 D.30种
二、多选题(每小题5分,少选得2分,错选不得分,共20分)
9.下列命题中正确的是( ).
A.标准差越小,则反映样本数据的离散程度越大
B.在回归直线方程中,当解释变量x每增加1个单位时,响应变量减少0.4个单位
C.对分类变量X与Y来说,它们的随机变量的值越小,“X与Y有关系”的把握程度越大
D.在回归分析模型中,相关系数绝对值越大,说明线性模型的拟合效果越好
10.下列说法正确的是( )
A.若,则
B.精确到0.1的近似值为1.6
C.被8除的余数为1
D.的展开式中含项的系数为5292
11.关于的说法,正确的是( )
A.展开式中的二项式系数之和为2048
B.展开式中只有第6项的二项式系数最大
C.展开式中第6项和第7项的二项式系数最大
D.展开式中第6项的系数最大
12.若,则下列结论正确的是( )
A. B. C. D.
三、填空题(每小题5分,共20分)
13.的展开式中的系数为___________.(用数字作答)
14.已知,t为常数,,且,则________.
15.二项式的展开式中的常数项是第项,则____________.
16..二项展开式,则___________,__________
四、解答题(本题共6小题,共70分)
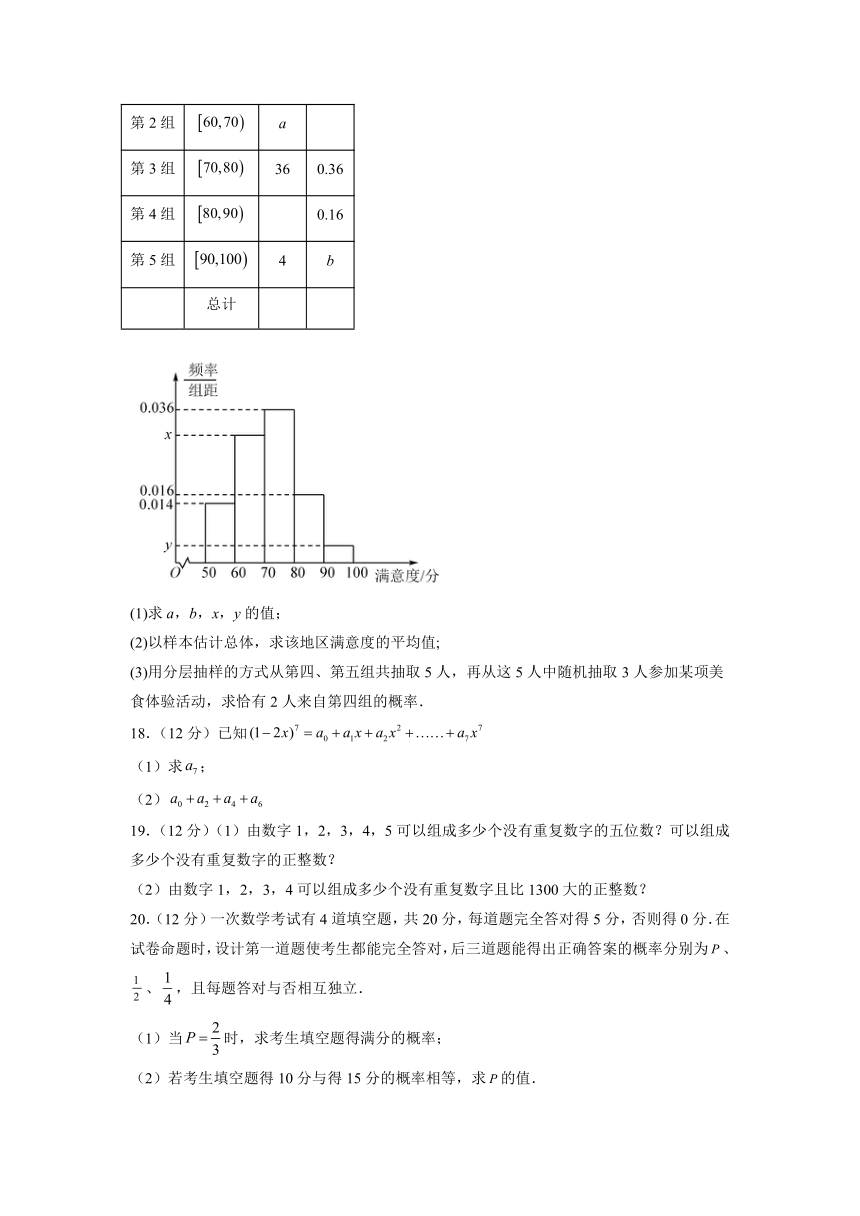
17.(10分)某餐饮公司为了了解最近半年期间,居民对其菜品的满意度(50分~100分),制定了一份问卷调查,并随机抽取了其中100份,制作了如下图所示的频率分布表及频率分布直方图,请以此为依据,回答下而的问题.
组别 分组 频数 频率
第1组 14 0.14
第2组 a
第3组 36 0.36
第4组 0.16
第5组 4 b
总计
(1)求a,b,x,y的值;
(2)以样本估计总体,求该地区满意度的平均值;
(3)用分层抽样的方式从第四、第五组共抽取5人,再从这5人中随机抽取3人参加某项美食体验活动,求恰有2人来自第四组的概率.
18.(12分)已知
(1)求;
(2)
19.(12分)(1)由数字1,2,3,4,5可以组成多少个没有重复数字的五位数?可以组成多少个没有重复数字的正整数?
(2)由数字1,2,3,4可以组成多少个没有重复数字且比1300大的正整数?
20.(12分)一次数学考试有4道填空题,共20分,每道题完全答对得5分,否则得0分.在试卷命题时,设计第一道题使考生都能完全答对,后三道题能得出正确答案的概率分别为、、,且每题答对与否相互独立.
(1)当时,求考生填空题得满分的概率;
(2)若考生填空题得10分与得15分的概率相等,求的值.
21.(12分)已知的展开式中各项的系数和比各项的二项式系数和大992.
(1)求展开式中的有理项;
(2)求展开式中系数最大的项.
22.(1)解不等式:;
(2)已知,求的值(用数字作答)
答案:
1.C 2.A 3.C 4.B 5.C 6.A 7.C 8.D 9.BD 10.AB 11.AC 12.ABD
13.15 14. 15.9 16. 80 31
17(1)由题设,则,故其对应频率为,即,
所以,即.
(2)由(1)及直方图知:平均值为55×0.14+65×0.3+75×0.36+85×0.16+95×0.04=71.6.
(3)由分层抽样的等比例性质知:从第四组抽取4人,从第五组抽取1人,
从5人中抽取3人共有种方法,恰有2人来自第四组共有种方法,
故恰有2人来自第四组的概率为0.6.
18.(1)∵是展开式中第8项的系数,
;
(2)令,得,
令,得,
两式相加:,
即.
19.(1)根据题意,将1,2,3,4,5进行全排列,
有种情况,即可以组成个没有重复数字的五位数.
要求由1,2,3,4,5组成没有重复数字的正整数,可以分种情况讨论:
①由5个数字组成的一位数,有种情况,
②由5个数字组成的两位数,有种情况,
③由5个数字组成的三位数,有种情况,
④由5个数字组成的四位数,有种情况,
⑤由5个数字组成的五位数,有种情况,
则一共有没有重复数字的正整数.
(2)根据题意分两种情况讨论:
①首位数字是2,3,4时, 组成的4位数都比1300大,
此时有种情况,
②首位数字是时,第二位数字必须为3,4时,
此时有种情况,
一共有种情况,即可以组成个比1300大的正整数.
20.设考生填空题得满分、15分、10分为事件A、B、C
(1)
(2)=
=
因为 , 所以=得
21.(1)令,则展开式中各项系数和为,展开式中的二项式系数和为,
依题意,,即,
整理得,所以,解得,
所以展开式通项为,
所以,时,
展开式中的有理项分别为,.
(2)由(1)知,展开式通项为,
令项的系数最大,则有,即,
整理得,解得,而,所以,
所以展开式中系数最大项为.
22.(1)因为,
所以,
所以,所以,
所以解集为;
(2)因为,
所以,
所以,
所以,所以,
解得或(舍),
所以
.
1.的展开式中的常数项为
A. B. C. D.
2.小林同学喜欢吃4种坚果:核桃 腰果 杏仁 榛子,他有5种颜色的“每日坚果”袋.每个袋子中至少装1种坚果,至多装4种坚果.小林同学希望五个袋子中所装坚果种类各不相同,且每一种坚果在袋子中出现的总次数均为偶数,那么不同的方案数为( )
A.20160 B.20220 C.20280 D.20340
3.如果的展开式中含有常数项,则正整数n的最小值是( )
A.3 B.4 C.5 D.6
4.若,则( )
A.27 B.-27 C.54 D.-54
5.现有十二生肖的吉祥物各一个,已知甲同学喜欢牛、马和猴的吉祥物,乙同学喜欢牛、狗和羊的吉祥物,丙同学对所有的吉祥物都喜欢,让甲、乙、丙三位同学依次从中选一个珍藏,若每个人所选取的礼物都是自己喜欢的,则不同的选法共有( )
A.50种 B.60种 C.80种 D.90种
6.名同学报名参加个活动小组,每人限报个活动小组,不同的报名方法种数为( )
A. B. C. D.
7.若的展开式中各项的二项式系数之和为512,且第6项的系数最大,则a的取值范围为( )
A. B.
C. D.
8.5名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排2名,则不同的安排方法共有( )
A.120种 B.90种 C.60种 D.30种
二、多选题(每小题5分,少选得2分,错选不得分,共20分)
9.下列命题中正确的是( ).
A.标准差越小,则反映样本数据的离散程度越大
B.在回归直线方程中,当解释变量x每增加1个单位时,响应变量减少0.4个单位
C.对分类变量X与Y来说,它们的随机变量的值越小,“X与Y有关系”的把握程度越大
D.在回归分析模型中,相关系数绝对值越大,说明线性模型的拟合效果越好
10.下列说法正确的是( )
A.若,则
B.精确到0.1的近似值为1.6
C.被8除的余数为1
D.的展开式中含项的系数为5292
11.关于的说法,正确的是( )
A.展开式中的二项式系数之和为2048
B.展开式中只有第6项的二项式系数最大
C.展开式中第6项和第7项的二项式系数最大
D.展开式中第6项的系数最大
12.若,则下列结论正确的是( )
A. B. C. D.
三、填空题(每小题5分,共20分)
13.的展开式中的系数为___________.(用数字作答)
14.已知,t为常数,,且,则________.
15.二项式的展开式中的常数项是第项,则____________.
16..二项展开式,则___________,__________
四、解答题(本题共6小题,共70分)
17.(10分)某餐饮公司为了了解最近半年期间,居民对其菜品的满意度(50分~100分),制定了一份问卷调查,并随机抽取了其中100份,制作了如下图所示的频率分布表及频率分布直方图,请以此为依据,回答下而的问题.
组别 分组 频数 频率
第1组 14 0.14
第2组 a
第3组 36 0.36
第4组 0.16
第5组 4 b
总计
(1)求a,b,x,y的值;
(2)以样本估计总体,求该地区满意度的平均值;
(3)用分层抽样的方式从第四、第五组共抽取5人,再从这5人中随机抽取3人参加某项美食体验活动,求恰有2人来自第四组的概率.
18.(12分)已知
(1)求;
(2)
19.(12分)(1)由数字1,2,3,4,5可以组成多少个没有重复数字的五位数?可以组成多少个没有重复数字的正整数?
(2)由数字1,2,3,4可以组成多少个没有重复数字且比1300大的正整数?
20.(12分)一次数学考试有4道填空题,共20分,每道题完全答对得5分,否则得0分.在试卷命题时,设计第一道题使考生都能完全答对,后三道题能得出正确答案的概率分别为、、,且每题答对与否相互独立.
(1)当时,求考生填空题得满分的概率;
(2)若考生填空题得10分与得15分的概率相等,求的值.
21.(12分)已知的展开式中各项的系数和比各项的二项式系数和大992.
(1)求展开式中的有理项;
(2)求展开式中系数最大的项.
22.(1)解不等式:;
(2)已知,求的值(用数字作答)
答案:
1.C 2.A 3.C 4.B 5.C 6.A 7.C 8.D 9.BD 10.AB 11.AC 12.ABD
13.15 14. 15.9 16. 80 31
17(1)由题设,则,故其对应频率为,即,
所以,即.
(2)由(1)及直方图知:平均值为55×0.14+65×0.3+75×0.36+85×0.16+95×0.04=71.6.
(3)由分层抽样的等比例性质知:从第四组抽取4人,从第五组抽取1人,
从5人中抽取3人共有种方法,恰有2人来自第四组共有种方法,
故恰有2人来自第四组的概率为0.6.
18.(1)∵是展开式中第8项的系数,
;
(2)令,得,
令,得,
两式相加:,
即.
19.(1)根据题意,将1,2,3,4,5进行全排列,
有种情况,即可以组成个没有重复数字的五位数.
要求由1,2,3,4,5组成没有重复数字的正整数,可以分种情况讨论:
①由5个数字组成的一位数,有种情况,
②由5个数字组成的两位数,有种情况,
③由5个数字组成的三位数,有种情况,
④由5个数字组成的四位数,有种情况,
⑤由5个数字组成的五位数,有种情况,
则一共有没有重复数字的正整数.
(2)根据题意分两种情况讨论:
①首位数字是2,3,4时, 组成的4位数都比1300大,
此时有种情况,
②首位数字是时,第二位数字必须为3,4时,
此时有种情况,
一共有种情况,即可以组成个比1300大的正整数.
20.设考生填空题得满分、15分、10分为事件A、B、C
(1)
(2)=
=
因为 , 所以=得
21.(1)令,则展开式中各项系数和为,展开式中的二项式系数和为,
依题意,,即,
整理得,所以,解得,
所以展开式通项为,
所以,时,
展开式中的有理项分别为,.
(2)由(1)知,展开式通项为,
令项的系数最大,则有,即,
整理得,解得,而,所以,
所以展开式中系数最大项为.
22.(1)因为,
所以,
所以,所以,
所以解集为;
(2)因为,
所以,
所以,
所以,所以,
解得或(舍),
所以
.
