二次函数应用题选讲[上学期]
图片预览






文档简介
课件15张PPT。1.有一抛物线形的拱形桥,其解析式为y=ax2,桥拱跨度为12m,桥高4m.按规定,通过该桥下的载货车最高处与桥拱之间的距离CD不得小于0.5m.今有一辆宽为3m,高为3m(载货最高处与地面AB的距离)的货车能否通过此桥孔?为什么?解:由题意知y=ax2过点(6,-4)解得∴ 抛物线的解析式为∴当x=1.5时,y=-0.25,即C离桥面0.25m。∵ DE=3.0m, ∴CD=4-0.25-3.0=0.75>0.5
∴能通过2.某公园草地的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设立柱。为计算所需钢管立柱的总长度,设计人员建立如下坐标系计算。
(1)求抛物线解析式; (2)自变量x的取值范围求;(3)总长度。(2)由图得A(-1,0),C(1,0),
所以x的取值范围为-1≤ x ≤ 1所以总长度为(0.32+0.48)×100=80(m)3.如图所示是我市一条高速公路上的隧道口在平面直角坐标系上的示意图,点A和点A1,点B和B1分别关于y轴对称,隧道拱部分BCB1为一段抛物线,最高点C离路面AA1的距离为8m,点B离路面AA1的距离为6m,隧道的宽AA1为16m.
(1)求隧道拱抛物线BCB1的解析式;
(2)现有一大型运货汽车,装载某大型设备后,其宽为4m,车载大型设备的顶部与路面距离为7m,它能否安全通过这个隧道?说明理由.答案: (1)(2)此车能安全通过隧道,
因为当时,设y=ax2+c(a≠ 0), ∵ B1(8,6),C(0,8)
∴解得4.一位篮球运动员跳起投篮,球沿抛物线
运行,然后准确落入篮框内.已知篮框中心离地面的距离为3.05m.
(1)球在空中运行的最大高度为多少m?
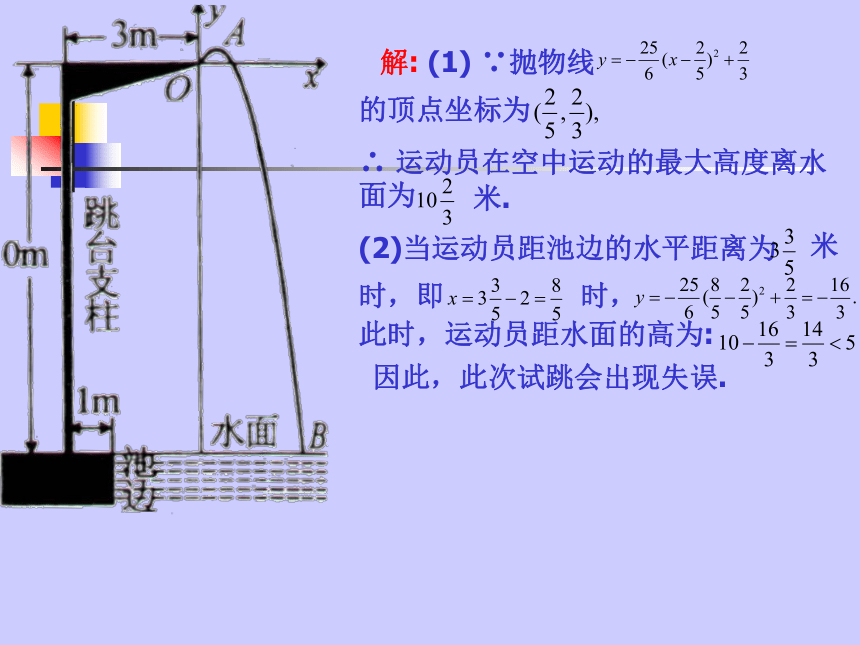
(2)如果该运动员跳投时,球出手离地面高度为2.25m,请问它距离篮框中心的水平距离是多少?5.某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是经过原点O的一条抛物线.在跳某规定动作时,正常情况下,该运动员在空中的最高处距水面32/3米,入水处距池边的距离为4米,同时,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为18/5米,问此次跳水会不会失误?并通过计算说明理由.解: (1) ∵抛物线的顶点坐标为∴ 运动员在空中运动的最大高度离水面为米.(2)当运动员距池边的水平距离为米时,即时,此时,运动员距水面的高为:因此,此次试跳会出现失误.6 如图所示,桃河公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.
(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外?
(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确到0.1m)?解:(1)如图,建立如图所示的坐标系,根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).设抛物线为y=a(x-h)2+k,由待定系数法可求得抛物线表达式为:y=-(x-1)2+2.25.当y=0时,可求得点C的坐标为(2.5,0);同理,点D的坐标为(-2.5,0).根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外. ●
C(2.5,0)●
D(-2.5,0)喷泉与二次函数由此可知,如果不计其它因素,那么水流的最大高度应达到约3.72m.解:(2)如图,根据题意得,A点坐标为(0,1.25),点C坐标为(3.5,0).或设抛物线为y=-x2+bx+c,由待定系数法可求得抛物线表达式为:y=-x2+22/7+5/4.设抛物线为y=-(x-h)2+k,由待定系数法可求得抛物线表达式为:y=-(x-11/7)2+729/196. ●
C(3.5,0)●
D(-3.5,0)●B(1.57,3.72)喷泉与二次函数7 如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关手y轴对称. ⑴钢缆的最低点到桥面的距离是少?
⑵两条钢缆最低点之间的距离是多少?
⑶你是怎样计算的?与同伴交流.⑴.钢缆的最低点到桥面的距离是少?你是怎样计算的?与同伴交流.可以将函数y=0.0225x2+0.9x+10配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;⑵两条钢缆最低点之间的距离是多少?你是怎样计算的?与同伴交流.想一想,你知道图中右面钢缆的表达式是什么吗? ⑶你还有其它方法吗?与同伴交流.直接利用顶点坐标公式再计算一下上面问题中钢缆的最低点到桥面的距离以及两条钢缆最低点之间的距离. 8 某学生推铅球,铅球出手(A点处)的高度是 m,出手后的铅球沿一段抛物线弧运行(如图),当运行到最大高度y=3m是,水平距离是x=4m.
(1)试求铅球行进高度y(m)与水平距离x(m)之间的函数关系式;
(2)如果将y轴平移至直线x=4,x轴平移到直线y=3,原抛物线不动,在新的坐标系下,求抛物线的函数关系式.解: (1)由已知可设抛物线的解析式为y=a(x-4)2+3(其中a<0), ∵抛物线经过点, ∴解得.故所求表达式为令y=0,即,解得x=-2或x=10(-2不不合题意,舍去).(2)原抛物线的顶点在新坐标系的原点,开口向下,且过点(-6,3),所以设抛物线的解析式为:y=ax2(a<0),则-3=36a,解得所以自变量的取值范围是0≤ x≤ 10.故所求的抛物线弧的函数表达式为9 某通讯公司销售一种市场需求较大的新型通讯产品,已知每件产品进价为40元,每年销售产品总开支(不含进价)总计120万元,在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在如图所示的一次函数关系式.
(1) 求y与x之间的函数关系式;
(2) 试写出该公司销售该种产品的年获利Z(万元)关于销售单价x(元)的函数关系式(年获利=年销售总额-年销售产品的总进价-年总开支),当销售单价x为何值时,年获利最大?最大利润为多少?
(3)若公司希望该种产品一年销售获利不低于40万元,借助一次函数图象,请你帮助该公司确定销售单价的范围,在此情况下,要使产品销量最大,你认为销售价应定为多少?
∴能通过2.某公园草地的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设立柱。为计算所需钢管立柱的总长度,设计人员建立如下坐标系计算。
(1)求抛物线解析式; (2)自变量x的取值范围求;(3)总长度。(2)由图得A(-1,0),C(1,0),
所以x的取值范围为-1≤ x ≤ 1所以总长度为(0.32+0.48)×100=80(m)3.如图所示是我市一条高速公路上的隧道口在平面直角坐标系上的示意图,点A和点A1,点B和B1分别关于y轴对称,隧道拱部分BCB1为一段抛物线,最高点C离路面AA1的距离为8m,点B离路面AA1的距离为6m,隧道的宽AA1为16m.
(1)求隧道拱抛物线BCB1的解析式;
(2)现有一大型运货汽车,装载某大型设备后,其宽为4m,车载大型设备的顶部与路面距离为7m,它能否安全通过这个隧道?说明理由.答案: (1)(2)此车能安全通过隧道,
因为当时,设y=ax2+c(a≠ 0), ∵ B1(8,6),C(0,8)
∴解得4.一位篮球运动员跳起投篮,球沿抛物线
运行,然后准确落入篮框内.已知篮框中心离地面的距离为3.05m.
(1)球在空中运行的最大高度为多少m?
(2)如果该运动员跳投时,球出手离地面高度为2.25m,请问它距离篮框中心的水平距离是多少?5.某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是经过原点O的一条抛物线.在跳某规定动作时,正常情况下,该运动员在空中的最高处距水面32/3米,入水处距池边的距离为4米,同时,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为18/5米,问此次跳水会不会失误?并通过计算说明理由.解: (1) ∵抛物线的顶点坐标为∴ 运动员在空中运动的最大高度离水面为米.(2)当运动员距池边的水平距离为米时,即时,此时,运动员距水面的高为:因此,此次试跳会出现失误.6 如图所示,桃河公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.
(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外?
(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确到0.1m)?解:(1)如图,建立如图所示的坐标系,根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).设抛物线为y=a(x-h)2+k,由待定系数法可求得抛物线表达式为:y=-(x-1)2+2.25.当y=0时,可求得点C的坐标为(2.5,0);同理,点D的坐标为(-2.5,0).根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外. ●
C(2.5,0)●
D(-2.5,0)喷泉与二次函数由此可知,如果不计其它因素,那么水流的最大高度应达到约3.72m.解:(2)如图,根据题意得,A点坐标为(0,1.25),点C坐标为(3.5,0).或设抛物线为y=-x2+bx+c,由待定系数法可求得抛物线表达式为:y=-x2+22/7+5/4.设抛物线为y=-(x-h)2+k,由待定系数法可求得抛物线表达式为:y=-(x-11/7)2+729/196. ●
C(3.5,0)●
D(-3.5,0)●B(1.57,3.72)喷泉与二次函数7 如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关手y轴对称. ⑴钢缆的最低点到桥面的距离是少?
⑵两条钢缆最低点之间的距离是多少?
⑶你是怎样计算的?与同伴交流.⑴.钢缆的最低点到桥面的距离是少?你是怎样计算的?与同伴交流.可以将函数y=0.0225x2+0.9x+10配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;⑵两条钢缆最低点之间的距离是多少?你是怎样计算的?与同伴交流.想一想,你知道图中右面钢缆的表达式是什么吗? ⑶你还有其它方法吗?与同伴交流.直接利用顶点坐标公式再计算一下上面问题中钢缆的最低点到桥面的距离以及两条钢缆最低点之间的距离. 8 某学生推铅球,铅球出手(A点处)的高度是 m,出手后的铅球沿一段抛物线弧运行(如图),当运行到最大高度y=3m是,水平距离是x=4m.
(1)试求铅球行进高度y(m)与水平距离x(m)之间的函数关系式;
(2)如果将y轴平移至直线x=4,x轴平移到直线y=3,原抛物线不动,在新的坐标系下,求抛物线的函数关系式.解: (1)由已知可设抛物线的解析式为y=a(x-4)2+3(其中a<0), ∵抛物线经过点, ∴解得.故所求表达式为令y=0,即,解得x=-2或x=10(-2不不合题意,舍去).(2)原抛物线的顶点在新坐标系的原点,开口向下,且过点(-6,3),所以设抛物线的解析式为:y=ax2(a<0),则-3=36a,解得所以自变量的取值范围是0≤ x≤ 10.故所求的抛物线弧的函数表达式为9 某通讯公司销售一种市场需求较大的新型通讯产品,已知每件产品进价为40元,每年销售产品总开支(不含进价)总计120万元,在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在如图所示的一次函数关系式.
(1) 求y与x之间的函数关系式;
(2) 试写出该公司销售该种产品的年获利Z(万元)关于销售单价x(元)的函数关系式(年获利=年销售总额-年销售产品的总进价-年总开支),当销售单价x为何值时,年获利最大?最大利润为多少?
(3)若公司希望该种产品一年销售获利不低于40万元,借助一次函数图象,请你帮助该公司确定销售单价的范围,在此情况下,要使产品销量最大,你认为销售价应定为多少?
