二次函数的应用[上学期]
图片预览



文档简介
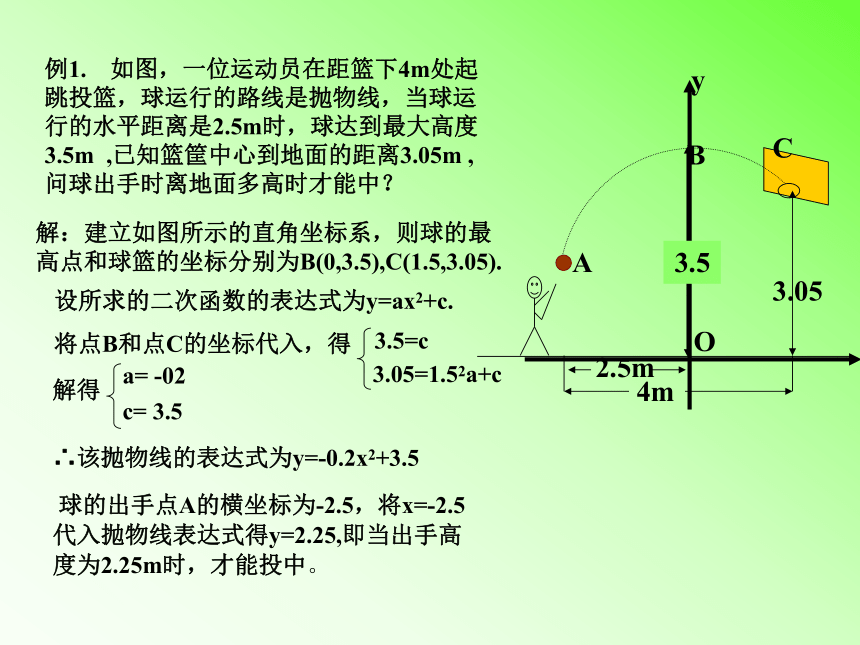
课件9张PPT。二次函数的应用篮球中的二次函数篮球例1. 如图,一位运动员在距篮下4m处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,球达到最大高度3.5m ,已知篮筐中心到地面的距离3.05m , 问球出手时离地面多高时才能中? 球的出手点A的横坐标为-2.5,将x=-2.5代入抛物线表达式得y=2.25,即当出手高度为2.25m时,才能投中。解:建立如图所示的直角坐标系,则球的最 高点和球篮的坐标分别为B(0,3.5),C(1.5,3.05).例2启明公司生产某种产品,每件产品成本是3元,售价是4元,
年销售量是10万件,为了获得更好的效益,公司准备拿出一定的
资金做广告,根据经验,每年投入的广告费是x(万元)时,产
品的年销售量将是原销售量的y倍,且y=﹣ x2+ x+ ,如果把
利润看作是销售总额减去成本费和广告费:
⑴试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广
告费是多少万元时,公司获得的年利润最大及最大年利润是多少
万元。
二次函数与商业利润⑵把①中的最大利润留出3万元做广告,其余资金投资新项目,现有六个项目可供选择,各项目每股投资金额和预计年收益如下表:
如果每个项目只能投一股,且要求所有投资项目的收益总额不低于1.6万元,问有几种符合要求的投资方式。写出每种投资方式所选的项目。
解:(2)用于再投资的资金是16-3=13(万元),经分析,有两种投资方式符合要求。一种是取A,B,E各一股,投入资金为5+2+6=13(万元),收益为0.55+0.4+0.9=1.85(万元)>1.6(万元);另一种是取B,D,E各一股,投入资金为2+4+6=12(万元)<13(万元),收益为0.4+0.5+0.9=1.8(万元)>(万元)。例3.小明的家门前有一块空地,空地外有一面长10米的围墙,为
了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买
回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的
方便,准备在花圃的中间再围出一条宽为一米的通道及在左右花
圃各放一个1米宽的门(木质)。
花圃的宽AD究竟应为多少米才能使花圃的面积最大?解:设AD=x,则AB=32-4x+3=35-4x
从而S=x(35-4x)-x=-4x2+34x
∵AB≤10 ∴6.25≤x
S=-4x2+34x,对称轴x=4.25,开口朝下
∴当x≥4.25时S随x的增大而减小
故当x=6.25时,S取最大值56.25
B二次函数与花园面积实际问题 数学问题求解数学问题小结二次函数与拱桥问题例3小明的家门前有一块空地,空地外有一面长10米的围墙,为
了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买
回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的
方便,准备在花圃的中间在围出一条宽为一米的通道及在左右花
圃各放一个1米宽的门(如图所示)。
花圃的宽AD究竟应为多少米才能使花圃的面积最大?DAHEGFCB解:设AD=x,则AB=32-4x+3=35-4x
从而S=x(35-4x)-x=-4x2+34x
∵AB≤10,
∴6.25≤x
S=-4x2+34x,对称轴x=4.25,开口朝下
∴当x≥4.25时S随x的增大而减小
故当x=6.25时,S取最大值56.25
二次函数与花园面积
年销售量是10万件,为了获得更好的效益,公司准备拿出一定的
资金做广告,根据经验,每年投入的广告费是x(万元)时,产
品的年销售量将是原销售量的y倍,且y=﹣ x2+ x+ ,如果把
利润看作是销售总额减去成本费和广告费:
⑴试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广
告费是多少万元时,公司获得的年利润最大及最大年利润是多少
万元。
二次函数与商业利润⑵把①中的最大利润留出3万元做广告,其余资金投资新项目,现有六个项目可供选择,各项目每股投资金额和预计年收益如下表:
如果每个项目只能投一股,且要求所有投资项目的收益总额不低于1.6万元,问有几种符合要求的投资方式。写出每种投资方式所选的项目。
解:(2)用于再投资的资金是16-3=13(万元),经分析,有两种投资方式符合要求。一种是取A,B,E各一股,投入资金为5+2+6=13(万元),收益为0.55+0.4+0.9=1.85(万元)>1.6(万元);另一种是取B,D,E各一股,投入资金为2+4+6=12(万元)<13(万元),收益为0.4+0.5+0.9=1.8(万元)>(万元)。例3.小明的家门前有一块空地,空地外有一面长10米的围墙,为
了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买
回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的
方便,准备在花圃的中间再围出一条宽为一米的通道及在左右花
圃各放一个1米宽的门(木质)。
花圃的宽AD究竟应为多少米才能使花圃的面积最大?解:设AD=x,则AB=32-4x+3=35-4x
从而S=x(35-4x)-x=-4x2+34x
∵AB≤10 ∴6.25≤x
S=-4x2+34x,对称轴x=4.25,开口朝下
∴当x≥4.25时S随x的增大而减小
故当x=6.25时,S取最大值56.25
B二次函数与花园面积实际问题 数学问题求解数学问题小结二次函数与拱桥问题例3小明的家门前有一块空地,空地外有一面长10米的围墙,为
了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买
回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的
方便,准备在花圃的中间在围出一条宽为一米的通道及在左右花
圃各放一个1米宽的门(如图所示)。
花圃的宽AD究竟应为多少米才能使花圃的面积最大?DAHEGFCB解:设AD=x,则AB=32-4x+3=35-4x
从而S=x(35-4x)-x=-4x2+34x
∵AB≤10,
∴6.25≤x
S=-4x2+34x,对称轴x=4.25,开口朝下
∴当x≥4.25时S随x的增大而减小
故当x=6.25时,S取最大值56.25
二次函数与花园面积
