第19章一次函数图像专题复习
文档属性
| 名称 | 第19章一次函数图像专题复习 |  | |
| 格式 | zip | ||
| 文件大小 | 426.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-15 19:22:19 | ||
图片预览



文档简介
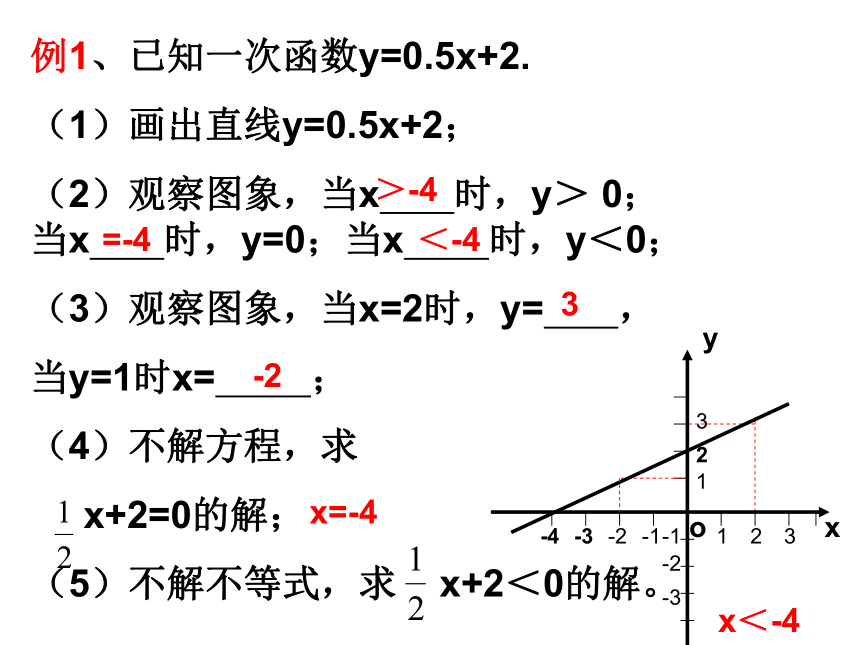
课件17张PPT。一次函数图像复习 函数图象能直观、形象地反映两个变量之间的关系。要善于观察图象中的所有信息,并能够熟练地转化成数学问题。导语1. 能利用图象求一次函数的解析式; 2 . 能借助图象解相应的方程和不等式; 3. 通过图象解有关面积问题; 4. 能借助图象解实际应用问题。复习目标例1、已知一次函数y=0.5x+2.
(1)画出直线y=0.5x+2;
(2)观察图象,当x 时,y> 0; 当x 时,y=0;当x 时,y<0;
(3)观察图象,当x=2时,y= ,
当y=1时x= ;
(4)不解方程,求
x+2=0的解;
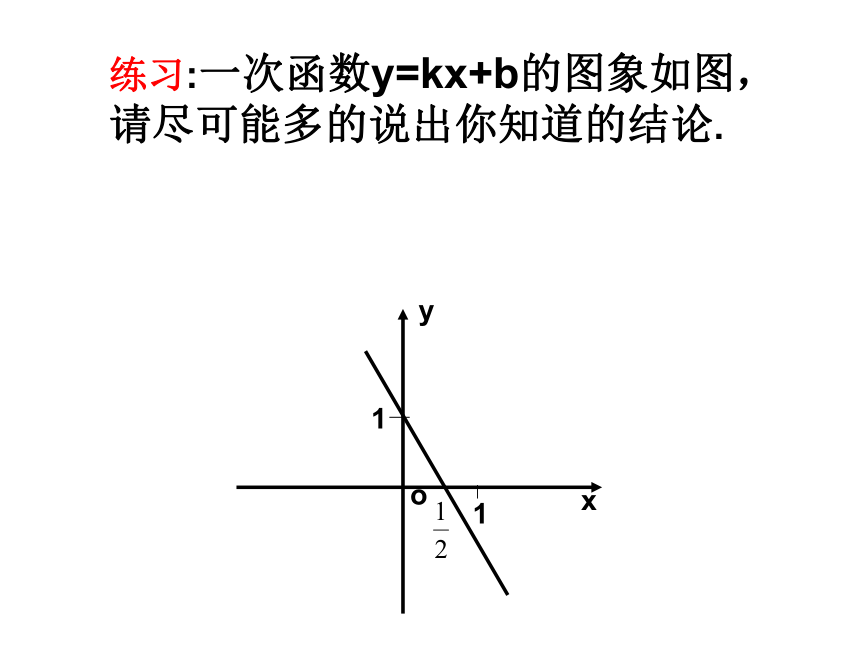
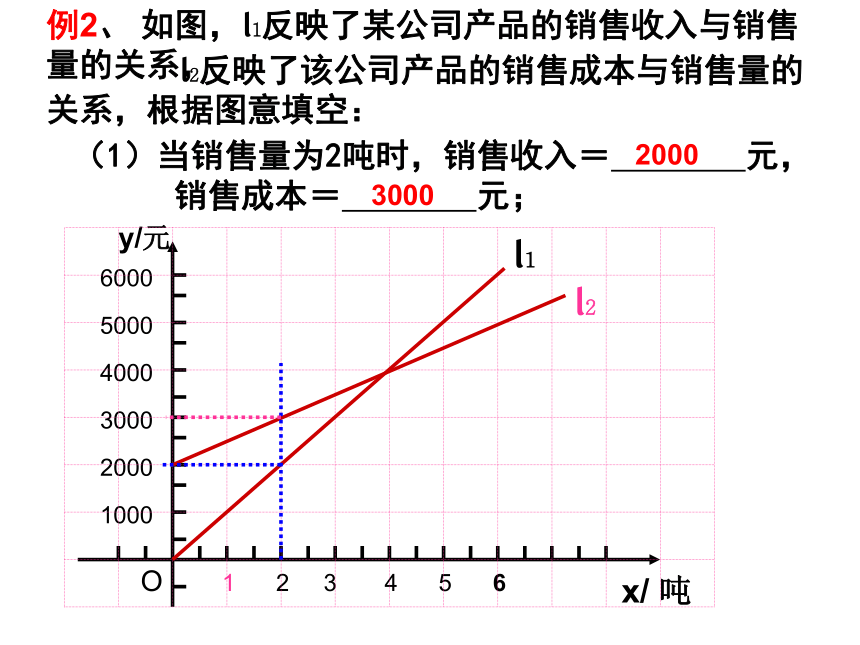
(5)不解不等式,求 x+2<0的解。xo-13-1-3>-4=-4<-43-2x=-4x<-4练习:一次函数y=kx+b的图象如图,请尽可能多的说出你知道的结论.xyo11例2、 如图,l1反映了某公司产品的销售收入与销售量的关系,(1)当销售量为2吨时,销售收入= 元,
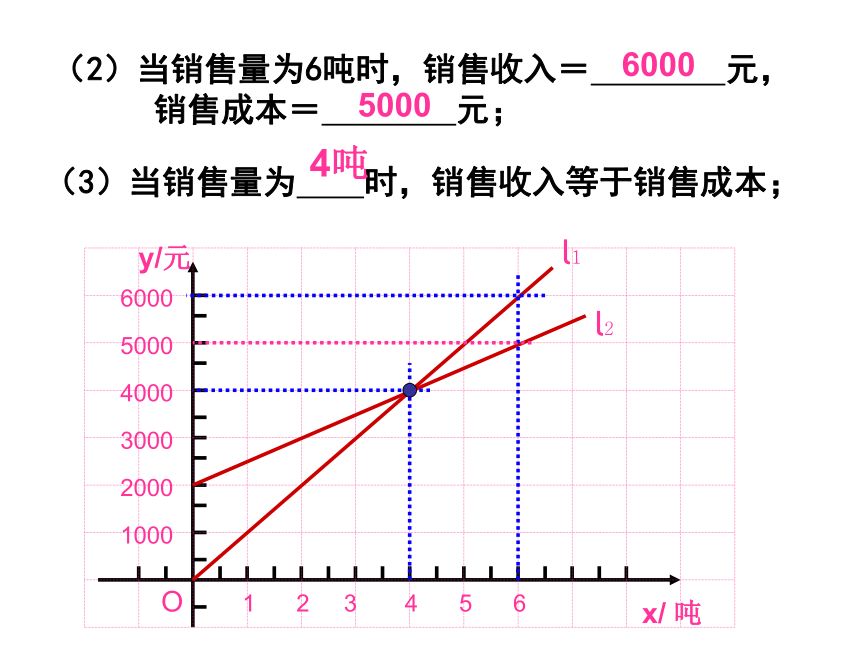
销售成本= 元;20003000 l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;60005000(3)当销售量为 时,销售收入等于销售成本;4吨(4)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);大于4吨小于4吨(5) l1对应的函数表达式是 ,
l2对应的函数表达式是 。y=1000xy=500x+2000练习、根据下列图象,你能说出哪些方程组的解?这些解是什么?例3 、 已知:函数 y = (m+1) x + 2 m﹣6
(1)若函数图象过(﹣1 ,2),求此函数的解析式。
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式。
(3)求满足(2)条件的直线与直线 y = ﹣3 x + 1 的交点,并
求这两条直线 与y 轴所围成的三角形面积 . 解:(1)由题意:
2=﹣(m+1)+2m﹣6解得 m = 9(2) 由题意,m +1= 2
解得 m = 1
∴ y = 2x﹣4(3) 由题意得∴ 这两直线的交点是(1 ,﹣2)y = 2x﹣4 与y 轴交于( 0 , - 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1)●11-4(1, ﹣2)S△=-2∴ y = 10x+12
解得:例四:某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的 图象如图所示。
(1)填空,月用电量为100度时,应交电费 元;
(2)当x≥100时求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?X(度)Y(元)100200204060O40y=0.2x+2072元例5:老师为了教学,需要在家上网查资料。电信公司 提供了两种上网收费方式:
方式 1 :按上网时间以每分钟 0.1 元计费;
方式 2 :月租费 20 元,再按上网时间 以每分钟 0.05 元计费。
请同学们帮老师选择:以何种方式上网更合算?oy/元x /分20400200y1 =0.1xy 2=0.05x+204030在同一坐标系中分别画出这两个函数的图像当 x = 400 时,
yA = yB当 x>400 时,
yA > yB当 0≤x<400 时,
yA < yB yA=0.1x yB=0.05x+20解:设上网时间为 x 分,若按方式 1 则收 元;
若按方式 2 则收 元。 yA=0.1x yB=0.05x+20练习:某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后,
(1)y与x之间的函数关系式。
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,
那么这个有效时间是多长?362100X(小时)y(微克) 3x,0(1)y=
, x≥2 4练习:已知直线y=kx+12和两坐标轴相交所围成的三角形的面积为24,求k的值解:由图象知,AO=12,根据面积得到,BO=4即B点坐标为(4,0)所以k= -3B的坐标还有可能为(-4,0)所以k= 3练习:已知直线y=-2x+6和y=x+3分别与x轴交于点A、B,且两直线交于点P(如图).(1)求点A、B及点P的坐标;(2)求△PAB的面积.ABPM解: (1)令y=0,则-2x+6=0和x+3=0,解得x=3和x=-3 ∴点 A(3,0)、 B(-3,0)∴点P的坐标为(1,4)(2)过点P作PM⊥x轴于M点,则PM=4,AB=|3-(-3)|=6,再见
(1)画出直线y=0.5x+2;
(2)观察图象,当x 时,y> 0; 当x 时,y=0;当x 时,y<0;
(3)观察图象,当x=2时,y= ,
当y=1时x= ;
(4)不解方程,求
x+2=0的解;
(5)不解不等式,求 x+2<0的解。xo-13-1-3>-4=-4<-43-2x=-4x<-4练习:一次函数y=kx+b的图象如图,请尽可能多的说出你知道的结论.xyo11例2、 如图,l1反映了某公司产品的销售收入与销售量的关系,(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;20003000 l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;60005000(3)当销售量为 时,销售收入等于销售成本;4吨(4)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);大于4吨小于4吨(5) l1对应的函数表达式是 ,
l2对应的函数表达式是 。y=1000xy=500x+2000练习、根据下列图象,你能说出哪些方程组的解?这些解是什么?例3 、 已知:函数 y = (m+1) x + 2 m﹣6
(1)若函数图象过(﹣1 ,2),求此函数的解析式。
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式。
(3)求满足(2)条件的直线与直线 y = ﹣3 x + 1 的交点,并
求这两条直线 与y 轴所围成的三角形面积 . 解:(1)由题意:
2=﹣(m+1)+2m﹣6解得 m = 9(2) 由题意,m +1= 2
解得 m = 1
∴ y = 2x﹣4(3) 由题意得∴ 这两直线的交点是(1 ,﹣2)y = 2x﹣4 与y 轴交于( 0 , - 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1)●11-4(1, ﹣2)S△=-2∴ y = 10x+12
解得:例四:某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的 图象如图所示。
(1)填空,月用电量为100度时,应交电费 元;
(2)当x≥100时求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?X(度)Y(元)100200204060O40y=0.2x+2072元例5:老师为了教学,需要在家上网查资料。电信公司 提供了两种上网收费方式:
方式 1 :按上网时间以每分钟 0.1 元计费;
方式 2 :月租费 20 元,再按上网时间 以每分钟 0.05 元计费。
请同学们帮老师选择:以何种方式上网更合算?oy/元x /分20400200y1 =0.1xy 2=0.05x+204030在同一坐标系中分别画出这两个函数的图像当 x = 400 时,
yA = yB当 x>400 时,
yA > yB当 0≤x<400 时,
yA < yB yA=0.1x yB=0.05x+20解:设上网时间为 x 分,若按方式 1 则收 元;
若按方式 2 则收 元。 yA=0.1x yB=0.05x+20练习:某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后,
(1)y与x之间的函数关系式。
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,
那么这个有效时间是多长?362100X(小时)y(微克) 3x,0
, x≥2 4练习:已知直线y=kx+12和两坐标轴相交所围成的三角形的面积为24,求k的值解:由图象知,AO=12,根据面积得到,BO=4即B点坐标为(4,0)所以k= -3B的坐标还有可能为(-4,0)所以k= 3练习:已知直线y=-2x+6和y=x+3分别与x轴交于点A、B,且两直线交于点P(如图).(1)求点A、B及点P的坐标;(2)求△PAB的面积.ABPM解: (1)令y=0,则-2x+6=0和x+3=0,解得x=3和x=-3 ∴点 A(3,0)、 B(-3,0)∴点P的坐标为(1,4)(2)过点P作PM⊥x轴于M点,则PM=4,AB=|3-(-3)|=6,再见
