第19章一次函数复习(经典.定义+图像性质题型)
文档属性
| 名称 | 第19章一次函数复习(经典.定义+图像性质题型) |  | |
| 格式 | zip | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-15 19:26:27 | ||
图片预览





文档简介
课件36张PPT。正比例函数和一次函数常见题型 一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。kx +b≠0 = 0≠0kx★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。1K≠0当m = ____时,函数
是一次函数.例题1:关于x的函
数y=(m-2)x +2+m是一次函数,则m=____
-2一、一次函数的识别
要注意考查全面,既要满足自变量x的最高次数为1;同时要满足自变量一次项系数不能为0。
例2.下列函数中,不是一次函数的是 ( )
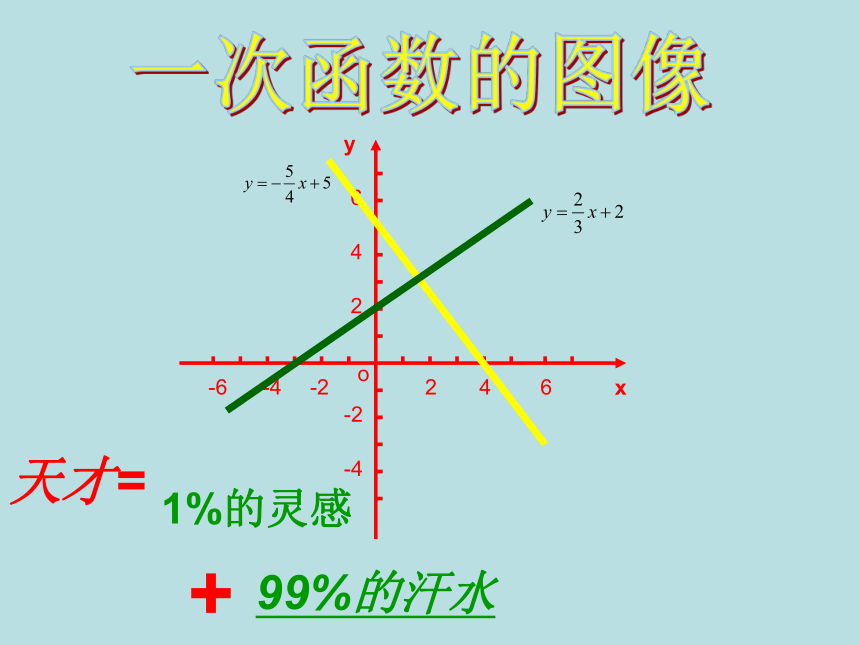
C-6o-4246246-2-2-4xy一次函数的图像天才=1%的灵感+99%的汗水一.复习:
1.作函数图像的步骤是什么?(1)列表 (2)描点 (3)连线2.一次函数图像的特点是什么?
是一条直线,所以我们在作一次图像
的时候只需要确定两个点,再过这两
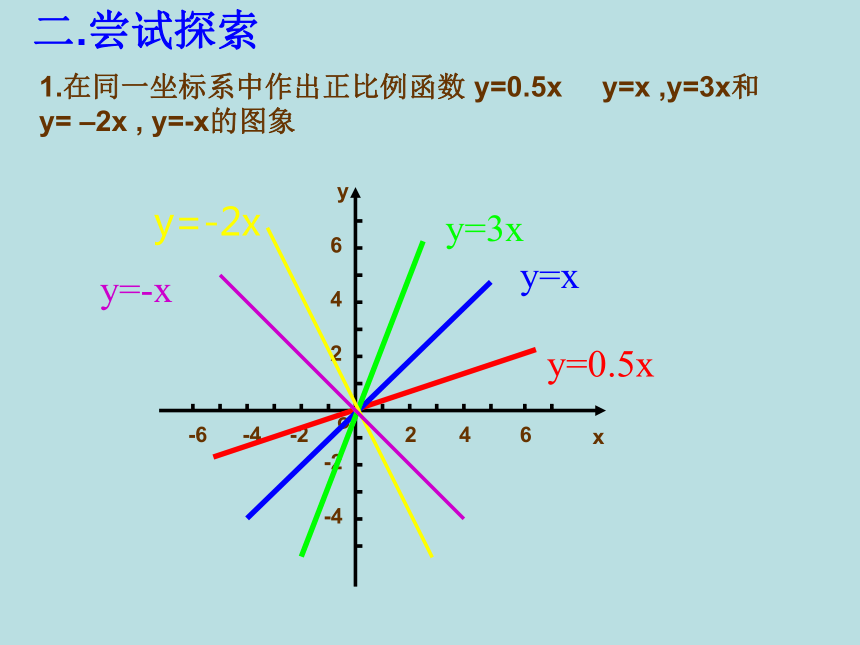
个点作直线就可以了。二.尝试探索1.在同一坐标系中作出正比例函数 y=0.5x y=x ,y=3x和
y= –2x , y=-x的图象-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2xy=-x-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2x(1)上面的函数都是什么函数?(2)正比例函数y=kx的
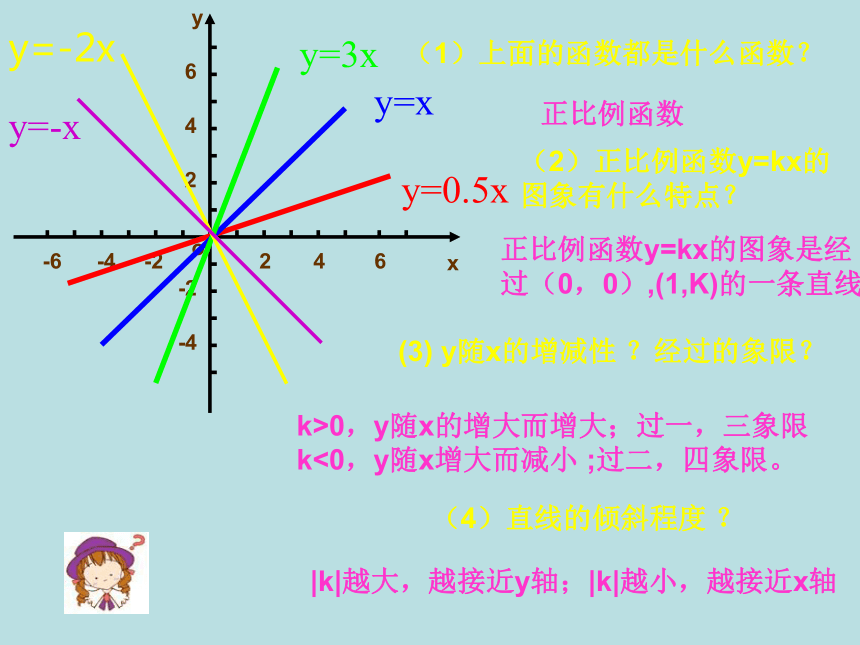
图象有什么特点?(3) y随x的增减性 ?经过的象限?(4)直线的倾斜程度 ? 正比例函数正比例函数y=kx的图象是经
过(0,0),(1,K)的一条直线k>0,y随x的增大而增大;过一,三象限
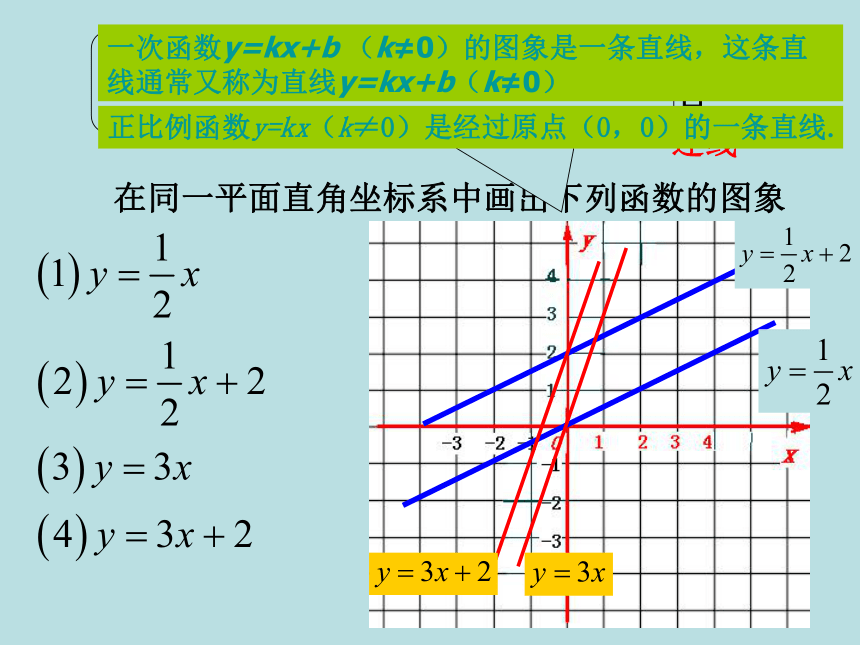
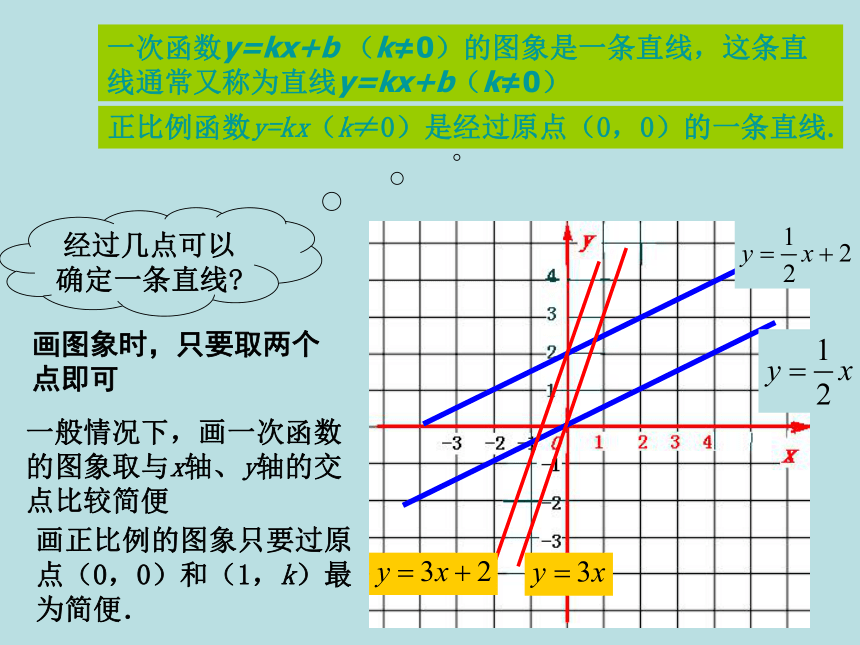
k<0,y随x增大而减小 ;过二,四象限。|k|越大,越接近y轴;|k|越小,越接近x轴y=-x作函数图象一般步骤是什么? 连线 列表描点在同一平面直角坐标系中画出下列函数的图象 你所画出的图象是什么形状? 一次函数y=kx+b (k≠0)的图象是一条直线,这条直线通常又称为直线y=kx+b(k≠0) 正比例函数y=kx(k≠0)是经过原点(0,0)的一条直线. 一次函数y=kx+b (k≠0)的图象是一条直线,这条直线通常又称为直线y=kx+b(k≠0) 正比例函数y=kx(k≠0)是经过原点(0,0)的一条直线. 经过几点可以确定一条直线? 画图象时,只要取两个点即可 一般情况下,画一次函数的图象取与x轴、y轴的交点比较简便 画正比例的图象只要过原点(0,0)和(1,k)最为简便.例1 在同一平面直角坐标系中画出下列
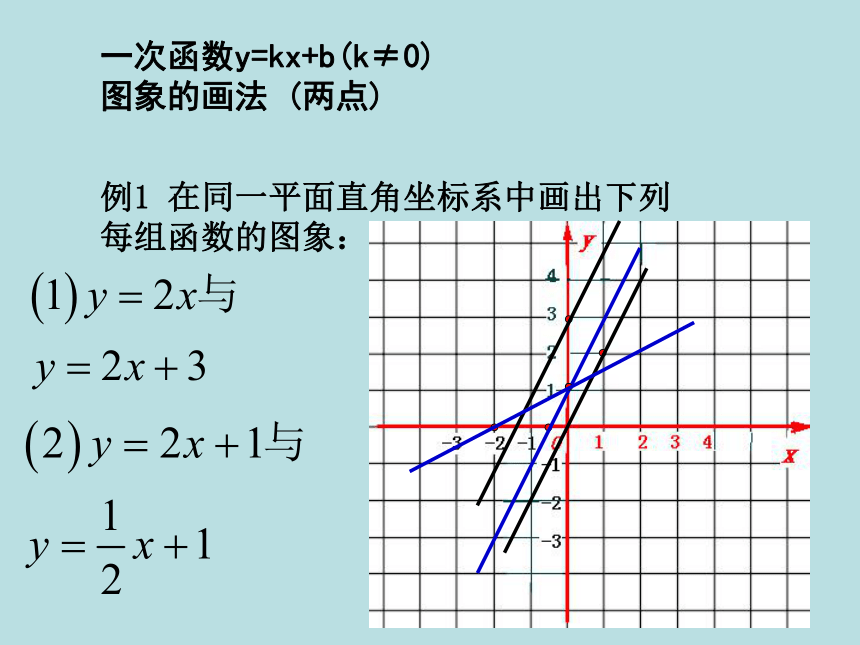
每组函数的图象: 一次函数y=kx+b(k≠0)
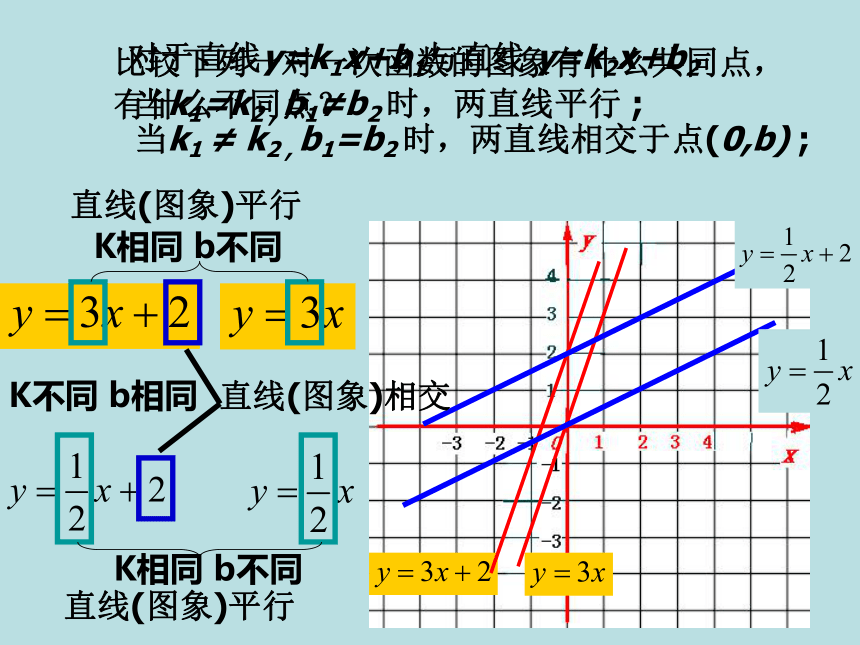
图象的画法 (两点)比较下列一对一次函数的图象有什么共同点,
有什么不同点? K相同 b不同K相同 b不同直线(图象)平行直线(图象)平行对于直线y=k1x+b1与直线 y=k2x+b2当k1=k2 , b1≠b2 时,两直线平行 ;K不同 b相同直线(图象)相交当k1 ≠ k2 , b1=b2 时,两直线相交于点(0,b) ;画出一次函数 的图象 31y30X观察分析: 当一个点在直线上从左向右移动时,它的位置怎样变化 自变量x由___到___函数y的值从___到___大小小大画出一次函数 的图象 31y30X观察分析: 自变量x由___到___函数y的值从___到___大小小大函数y=3x-2的图象是否也有这种现象 y随x的增大而增大,
这时函数的图象从左到右上升; 结论的图象 观察分析: 自变量x由___到___函数y的值从___到___大小小大y随x的增大而减小,
这时函数的图象从左到右下降; 结论一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降增大上升五.想一想 1)x从0开始逐渐增
大时,y=2x+6和y=5x
哪一个的值先达到20?
这说明了什么?-15o-10101551015-5-5-10x205yy=5x
y=2x+6
你看出来了吗?(2)直线y=-x与y=-x+6的位置关系如何?-6o-446246-2-2-4xy2y=-x+6y=-x平行(3)直线y=2x+6与y=-x+6的位置关系如何?-6o-446246-2-2-4xy2y=-x+6y=2x+6相交六.探索发现(1) 在同一坐标系中作出下列函数的图象
(1)(2)(3)-3o-223123-1-1-2xy1思考:k,b的值跟图像有什么关系?-(2)在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1做了这三个图像你发现了
K,b跟图像的关系吗?思考结论K>ob=0b>0b<0b=0b>0b<0通过作以上一次函数的图像我们发现y=kx+b
中,k,b的取值跟图像的关系如下:K<0一,三一,二,三一,三,四二,四一,二,四二,三,四当k>0时,y的值随x的增大而增大当k<0时,y的值随x的增大而减小(3)1.下列一次函数中,y的值随x的增大
而减小的有________。(3)(4)(2) (4)(1) y=10x-9(2) y=-0.3x+2二、一次函数的图像和性质2.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )(A)(B)(C)(D)B历史使人聪明,诗歌使人机智,数学使人精细。3.如果一次函数y=kx-3k+6的图象经
过原点,那么k的值为_________。4.写出m的3个值,使相应的一次函数
y = (2m-1)x+2的值都是随x的增大而减小.K=2可以写无数个,只要满足2m-1<0就可以了。例如:m=0.m=-1,m=-2变式训练②是正比例函数,而且对于它的每一组非零的对应
值(x,y)有xy<0。2、若一次函数 y=kx+1(k为常数,k ) 的图象经过第一、二、三象限,则k的取值范围是 . ≠03、在同一坐标系内,如图所示,直线
L1∶y=(k-2)x+k和L2∶y=kx的位置不可能为 ( )
A4、已知 y =(m – 1)x + m – 4 ,m为何值时
(1)它是一次函数;
(2)y随x的增大而减小;
(3)与y = – 2x – 3平行 ;
(4)函数图象过原点;
(5)函数图象不过第二象限;解: (1)∵它是一次函数 ∴ m – 1 ≠0 即m ≠ 1(2) ∵ y随x的增大而减小 ∴m – 1 < 0 即 m < 1 (3)∵它与y = – 2x – 3平行 ∴ m– 1 = – 2即m = – 1 (4)∵函数图象过原点 ∴ m – 4 = 0
即m = 4 (5)∵函数图象不过第二象限 ∴ m – 1 > 0 且m – 4 < 0 关于确定函数的解析式用“待定系数法”确定解析式(1)根据已知条件写出含有待定系数的解析式(定型)(2)将x,y的几对值或图象上点的坐标代入上述解析式,
得到以待定系数为未知数的方程或方程组,并解
方程(组),得到待定的系数的值 (定系数)(3)将求出的待定系数代回所求的函数关系式中,得到
所求函数的解析式 (定式)求一次函数的解析式,只要确定k和b两个常数即可;
求正比例函数或反比例函数的解析式,只要确定k
一个系数即可。关于确定函数的解析式确定一次函数解析式的三种条件,四种基本类型三种条件(1)与已知直线平行 (确定k);(2)在y轴上的截距 (确定b);(3)知道函数过的点 (把已知点坐标代入)。四种类型(1)过两点(2)过一点且与已知直线平行(3)过一点且知道截距(4)知道截距与已知直线平行三、待定系数法求函数解析式1、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式。∴一次函数的解析式为 y= - x+6。点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。2、已知 y – 2与x成正比,当x = 3时,y = 1
求(1)y 与x 的函数关系式;
(2)当x = 6时,y的值;
(3)当y = 8时,x的值;
(4)x为何值时,y > 0.变式训练①y与x-1成正比例,当x=2y=3时,求解析式②若直线y=ax+b过点(1,2)和(0,-1),求解析式③直线y=kx+b与y=3x平行,且过(1,2),求解析式④某一次函数的图象过点(-1,2),且函数y的值随x增大而减小,试写出一个符合上述条件的函数关系式能力提高已知一次函数的图象如图所示:
(1)求出此一次函数的解析式;
(2)观察图象,当x 时,y> 0; 当x 时,y=0;当x 时,y<0;
(3)观察图象,当x=2时,y= ,
当y=1时x= ;
(4)解方程,求
x+2=0的解;
(5)解不等式,求 x+2<0的解。xyo123-1-2-3123-4-1-2-3>-4=-4<-43-2y= x+2x=-4x<-4中考真题演练1.(贵阳中考)如图,已知
一次函数y=kx+b的图像,
当x<0,y的取值范围是( )
A.y>0 B.y<0
C.-20,则这个函数的图像一定经过
第 象限. 二、三、四3.已知一次函数y=kx+b的自变量x的取值范围是-2≤x≤6,相应的y值范围是-11≤y≤9,则此函数解析式为: . y=5x/2-6或y=-5x/2+4
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。1K≠0当m = ____时,函数
是一次函数.例题1:关于x的函
数y=(m-2)x +2+m是一次函数,则m=____
-2一、一次函数的识别
要注意考查全面,既要满足自变量x的最高次数为1;同时要满足自变量一次项系数不能为0。
例2.下列函数中,不是一次函数的是 ( )
C-6o-4246246-2-2-4xy一次函数的图像天才=1%的灵感+99%的汗水一.复习:
1.作函数图像的步骤是什么?(1)列表 (2)描点 (3)连线2.一次函数图像的特点是什么?
是一条直线,所以我们在作一次图像
的时候只需要确定两个点,再过这两
个点作直线就可以了。二.尝试探索1.在同一坐标系中作出正比例函数 y=0.5x y=x ,y=3x和
y= –2x , y=-x的图象-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2xy=-x-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2x(1)上面的函数都是什么函数?(2)正比例函数y=kx的
图象有什么特点?(3) y随x的增减性 ?经过的象限?(4)直线的倾斜程度 ? 正比例函数正比例函数y=kx的图象是经
过(0,0),(1,K)的一条直线k>0,y随x的增大而增大;过一,三象限
k<0,y随x增大而减小 ;过二,四象限。|k|越大,越接近y轴;|k|越小,越接近x轴y=-x作函数图象一般步骤是什么? 连线 列表描点在同一平面直角坐标系中画出下列函数的图象 你所画出的图象是什么形状? 一次函数y=kx+b (k≠0)的图象是一条直线,这条直线通常又称为直线y=kx+b(k≠0) 正比例函数y=kx(k≠0)是经过原点(0,0)的一条直线. 一次函数y=kx+b (k≠0)的图象是一条直线,这条直线通常又称为直线y=kx+b(k≠0) 正比例函数y=kx(k≠0)是经过原点(0,0)的一条直线. 经过几点可以确定一条直线? 画图象时,只要取两个点即可 一般情况下,画一次函数的图象取与x轴、y轴的交点比较简便 画正比例的图象只要过原点(0,0)和(1,k)最为简便.例1 在同一平面直角坐标系中画出下列
每组函数的图象: 一次函数y=kx+b(k≠0)
图象的画法 (两点)比较下列一对一次函数的图象有什么共同点,
有什么不同点? K相同 b不同K相同 b不同直线(图象)平行直线(图象)平行对于直线y=k1x+b1与直线 y=k2x+b2当k1=k2 , b1≠b2 时,两直线平行 ;K不同 b相同直线(图象)相交当k1 ≠ k2 , b1=b2 时,两直线相交于点(0,b) ;画出一次函数 的图象 31y30X观察分析: 当一个点在直线上从左向右移动时,它的位置怎样变化 自变量x由___到___函数y的值从___到___大小小大画出一次函数 的图象 31y30X观察分析: 自变量x由___到___函数y的值从___到___大小小大函数y=3x-2的图象是否也有这种现象 y随x的增大而增大,
这时函数的图象从左到右上升; 结论的图象 观察分析: 自变量x由___到___函数y的值从___到___大小小大y随x的增大而减小,
这时函数的图象从左到右下降; 结论一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降增大上升五.想一想 1)x从0开始逐渐增
大时,y=2x+6和y=5x
哪一个的值先达到20?
这说明了什么?-15o-10101551015-5-5-10x205yy=5x
y=2x+6
你看出来了吗?(2)直线y=-x与y=-x+6的位置关系如何?-6o-446246-2-2-4xy2y=-x+6y=-x平行(3)直线y=2x+6与y=-x+6的位置关系如何?-6o-446246-2-2-4xy2y=-x+6y=2x+6相交六.探索发现(1) 在同一坐标系中作出下列函数的图象
(1)(2)(3)-3o-223123-1-1-2xy1思考:k,b的值跟图像有什么关系?-(2)在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1做了这三个图像你发现了
K,b跟图像的关系吗?思考结论K>ob=0b>0b<0b=0b>0b<0通过作以上一次函数的图像我们发现y=kx+b
中,k,b的取值跟图像的关系如下:K<0一,三一,二,三一,三,四二,四一,二,四二,三,四当k>0时,y的值随x的增大而增大当k<0时,y的值随x的增大而减小(3)1.下列一次函数中,y的值随x的增大
而减小的有________。(3)(4)(2) (4)(1) y=10x-9(2) y=-0.3x+2二、一次函数的图像和性质2.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )(A)(B)(C)(D)B历史使人聪明,诗歌使人机智,数学使人精细。3.如果一次函数y=kx-3k+6的图象经
过原点,那么k的值为_________。4.写出m的3个值,使相应的一次函数
y = (2m-1)x+2的值都是随x的增大而减小.K=2可以写无数个,只要满足2m-1<0就可以了。例如:m=0.m=-1,m=-2变式训练②是正比例函数,而且对于它的每一组非零的对应
值(x,y)有xy<0。2、若一次函数 y=kx+1(k为常数,k ) 的图象经过第一、二、三象限,则k的取值范围是 . ≠03、在同一坐标系内,如图所示,直线
L1∶y=(k-2)x+k和L2∶y=kx的位置不可能为 ( )
A4、已知 y =(m – 1)x + m – 4 ,m为何值时
(1)它是一次函数;
(2)y随x的增大而减小;
(3)与y = – 2x – 3平行 ;
(4)函数图象过原点;
(5)函数图象不过第二象限;解: (1)∵它是一次函数 ∴ m – 1 ≠0 即m ≠ 1(2) ∵ y随x的增大而减小 ∴m – 1 < 0 即 m < 1 (3)∵它与y = – 2x – 3平行 ∴ m– 1 = – 2即m = – 1 (4)∵函数图象过原点 ∴ m – 4 = 0
即m = 4 (5)∵函数图象不过第二象限 ∴ m – 1 > 0 且m – 4 < 0 关于确定函数的解析式用“待定系数法”确定解析式(1)根据已知条件写出含有待定系数的解析式(定型)(2)将x,y的几对值或图象上点的坐标代入上述解析式,
得到以待定系数为未知数的方程或方程组,并解
方程(组),得到待定的系数的值 (定系数)(3)将求出的待定系数代回所求的函数关系式中,得到
所求函数的解析式 (定式)求一次函数的解析式,只要确定k和b两个常数即可;
求正比例函数或反比例函数的解析式,只要确定k
一个系数即可。关于确定函数的解析式确定一次函数解析式的三种条件,四种基本类型三种条件(1)与已知直线平行 (确定k);(2)在y轴上的截距 (确定b);(3)知道函数过的点 (把已知点坐标代入)。四种类型(1)过两点(2)过一点且与已知直线平行(3)过一点且知道截距(4)知道截距与已知直线平行三、待定系数法求函数解析式1、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式。∴一次函数的解析式为 y= - x+6。点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。2、已知 y – 2与x成正比,当x = 3时,y = 1
求(1)y 与x 的函数关系式;
(2)当x = 6时,y的值;
(3)当y = 8时,x的值;
(4)x为何值时,y > 0.变式训练①y与x-1成正比例,当x=2y=3时,求解析式②若直线y=ax+b过点(1,2)和(0,-1),求解析式③直线y=kx+b与y=3x平行,且过(1,2),求解析式④某一次函数的图象过点(-1,2),且函数y的值随x增大而减小,试写出一个符合上述条件的函数关系式能力提高已知一次函数的图象如图所示:
(1)求出此一次函数的解析式;
(2)观察图象,当x 时,y> 0; 当x 时,y=0;当x 时,y<0;
(3)观察图象,当x=2时,y= ,
当y=1时x= ;
(4)解方程,求
x+2=0的解;
(5)解不等式,求 x+2<0的解。xyo123-1-2-3123-4-1-2-3>-4=-4<-43-2y= x+2x=-4x<-4中考真题演练1.(贵阳中考)如图,已知
一次函数y=kx+b的图像,
当x<0,y的取值范围是( )
A.y>0 B.y<0
C.-2
第 象限. 二、三、四3.已知一次函数y=kx+b的自变量x的取值范围是-2≤x≤6,相应的y值范围是-11≤y≤9,则此函数解析式为: . y=5x/2-6或y=-5x/2+4
