§3.3圆周角与圆心角的关系[下学期]
文档属性
| 名称 | §3.3圆周角与圆心角的关系[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 656.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-21 22:51:00 | ||
图片预览

文档简介
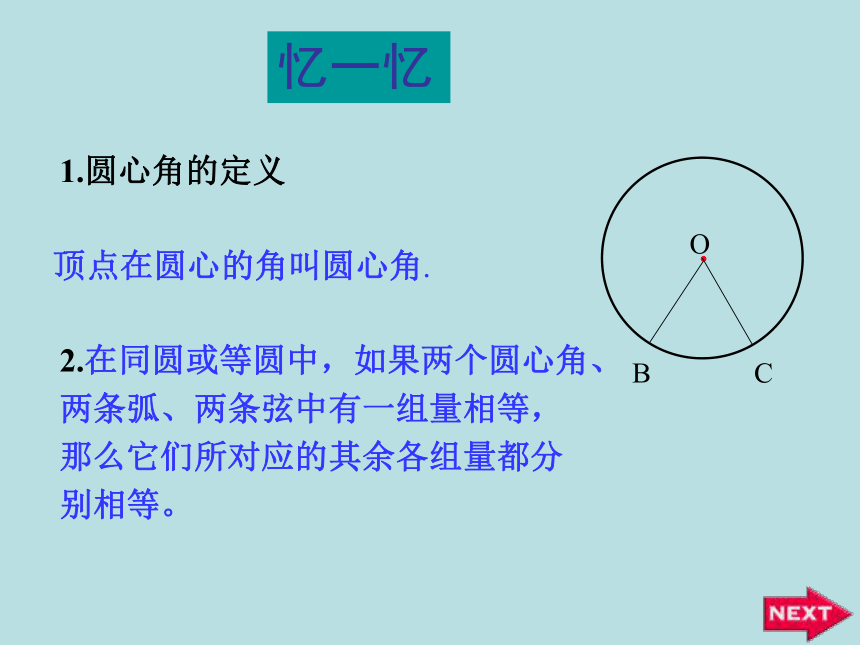
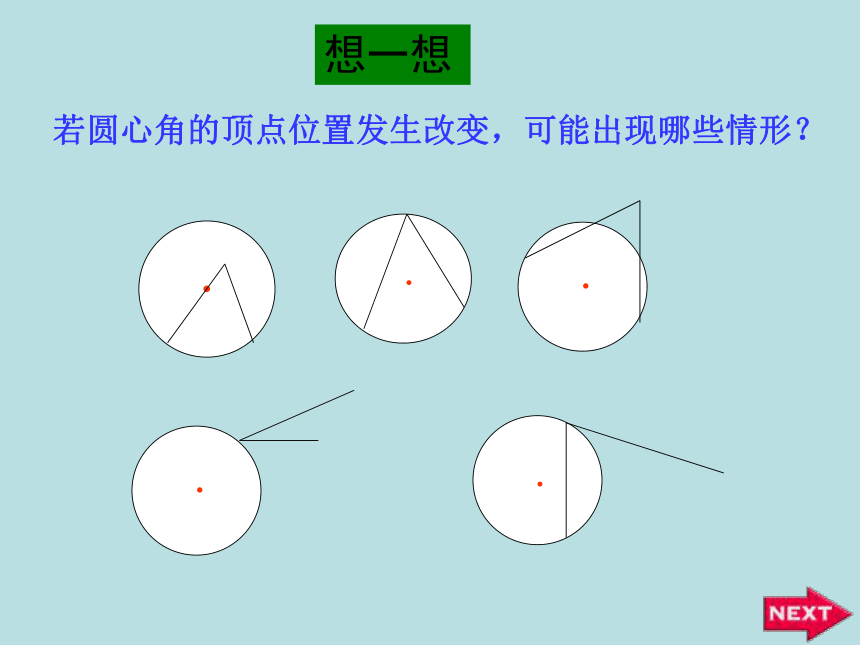
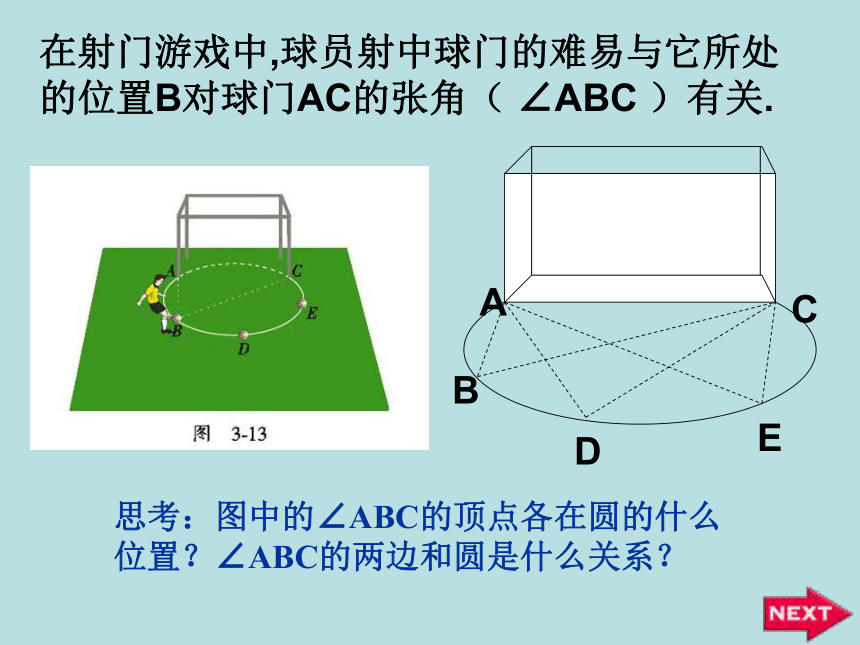
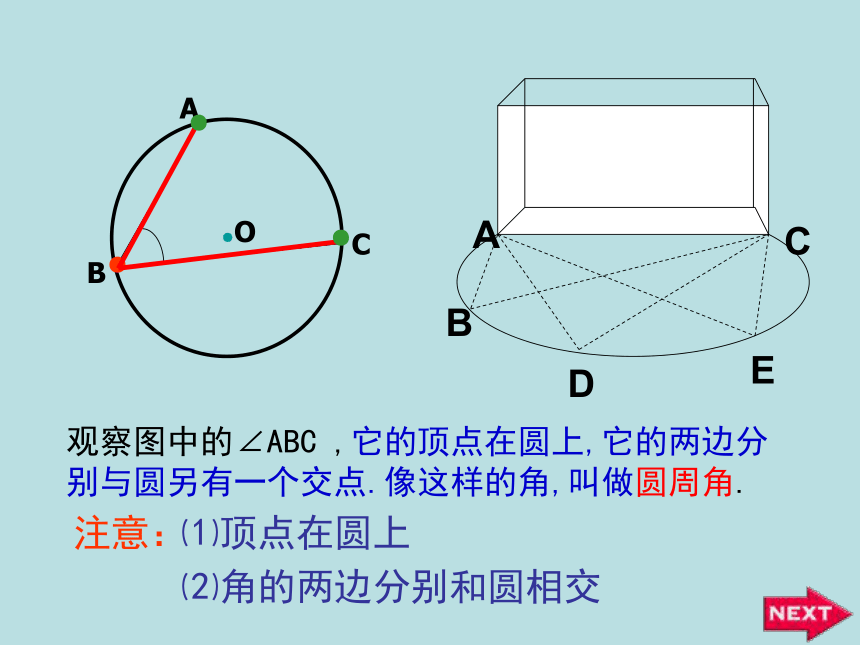
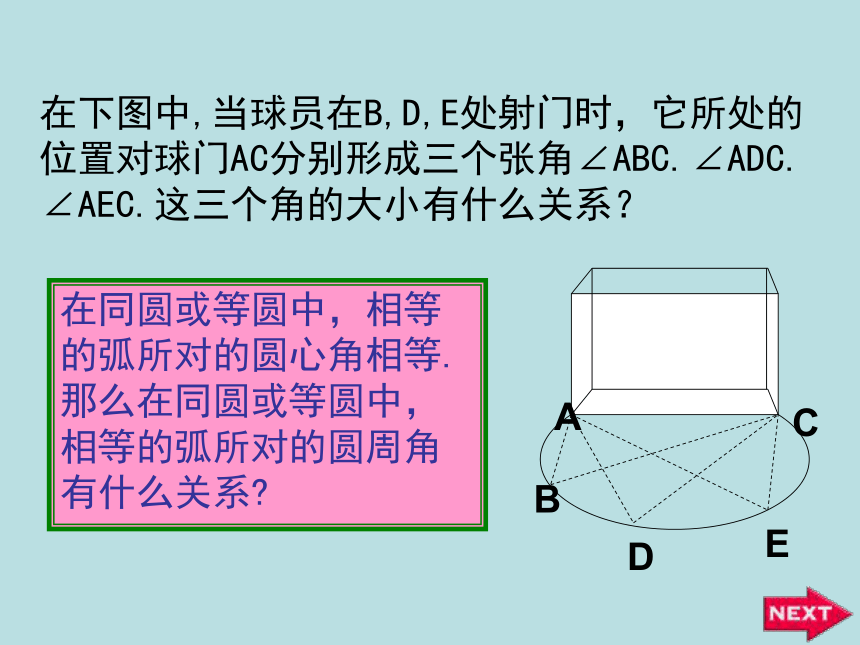
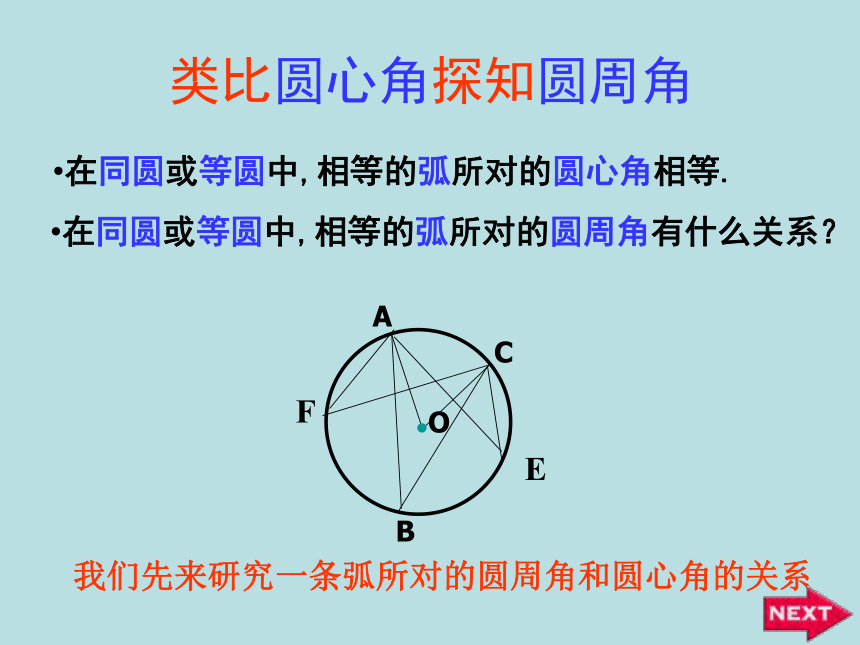
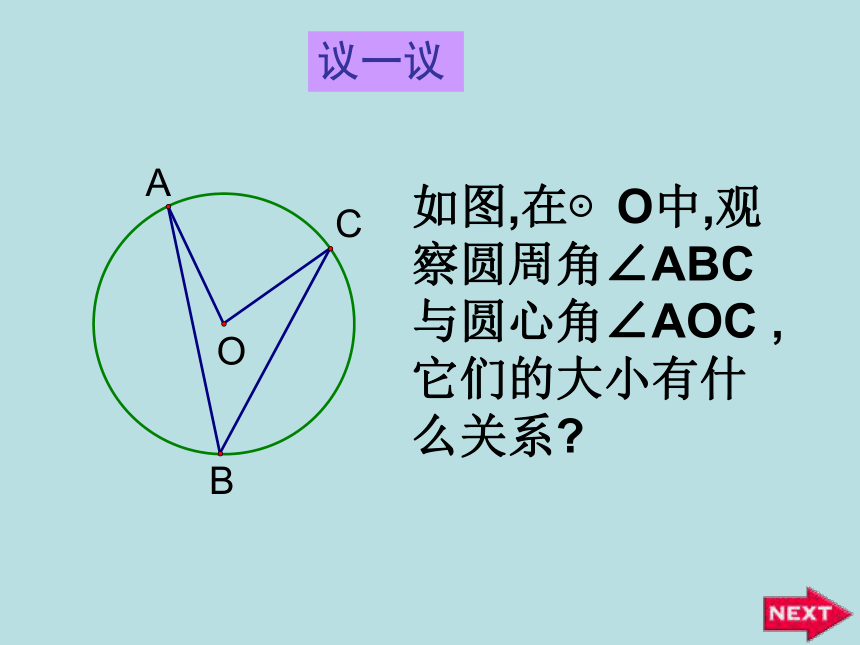
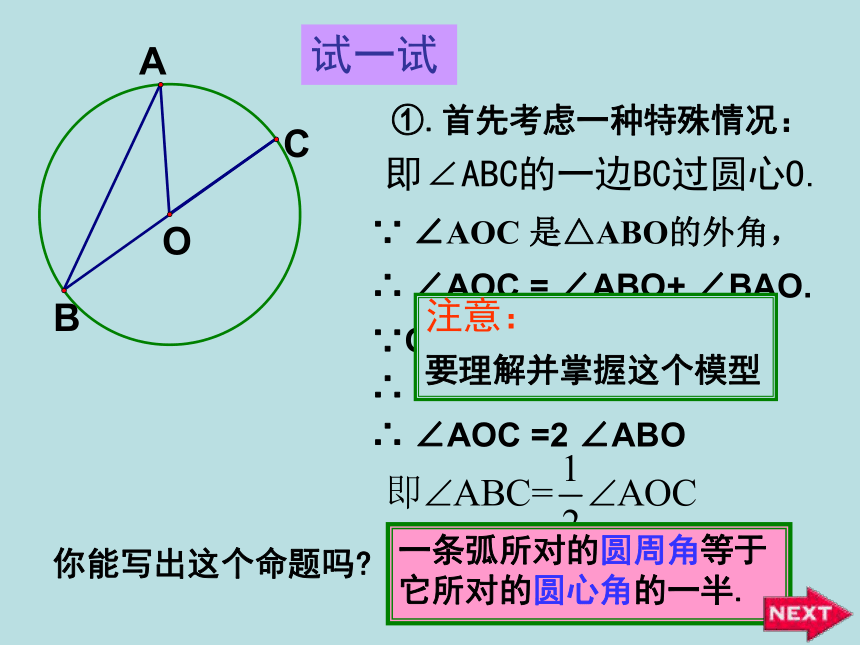
课件42张PPT。OABC圆周角和圆心角的关系明港二中王玲1.圆心角的定义顶点在圆心的角叫圆心角.2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。忆一忆若圆心角的顶点位置发生改变,可能出现哪些情形?想一想在射门游戏中,球员射中球门的难易与它所处的位置B对球门AC的张角( ∠ABC )有关.思考:图中的∠ABC的顶点各在圆的什么位置?∠ABC的两边和圆是什么关系?观察图中的∠ABC ,它的顶点在圆上,它的两边分别与圆另有一个交点.像这样的角,叫做圆周角.⑵角的两边分别和圆相交●注意:⑴顶点在圆上●●在下图中,当球员在B,D,E处射门时,它所处的位置对球门AC分别形成三个张角∠ABC.∠ADC. ∠AEC.这三个角的大小有什么关系?在同圆或等圆中,相等的弧所对的圆心角相等.那么在同圆或等圆中,相等的弧所对的圆周角有什么关系?类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系?我们先来研究一条弧所对的圆周角和圆心角的关系如图,在⊙O中,观察圆周角∠ABC 与圆心角∠AOC ,它们的大小有什么关系?OACB议一议即∠ABC的一边BC过圆心O.∵ ∠AOC 是△ABO的外角, ∴ ∠AOC = ∠ABO+ ∠BAO.∵OA=OB∴ ∠ABO = ∠BAO∴ ∠AOC =2 ∠ABOOACB你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.①.首先考虑一种特殊情况:注意:
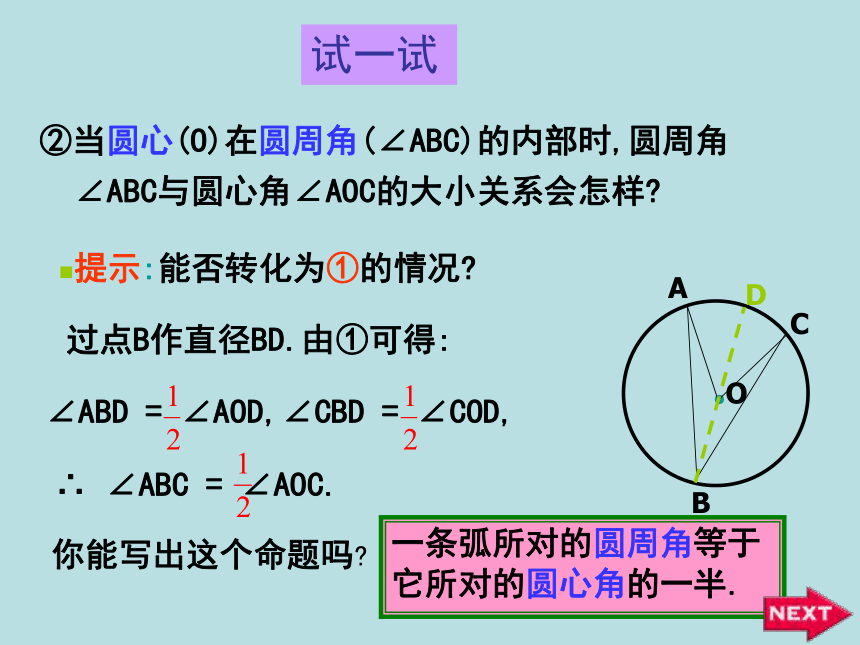
要理解并掌握这个模型试一试②当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样?
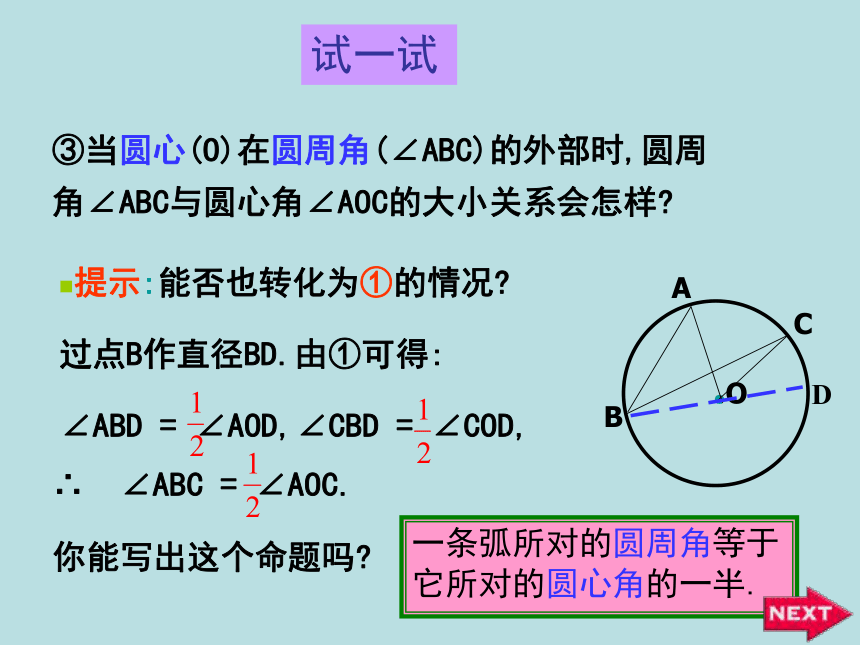
提示:能否转化为①的情况?过点B作直径BD.由①可得:∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.试一试③当圆心(O)在圆周角(∠ABC)的外部时,圆周
角∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否也转化为①的情况?
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于
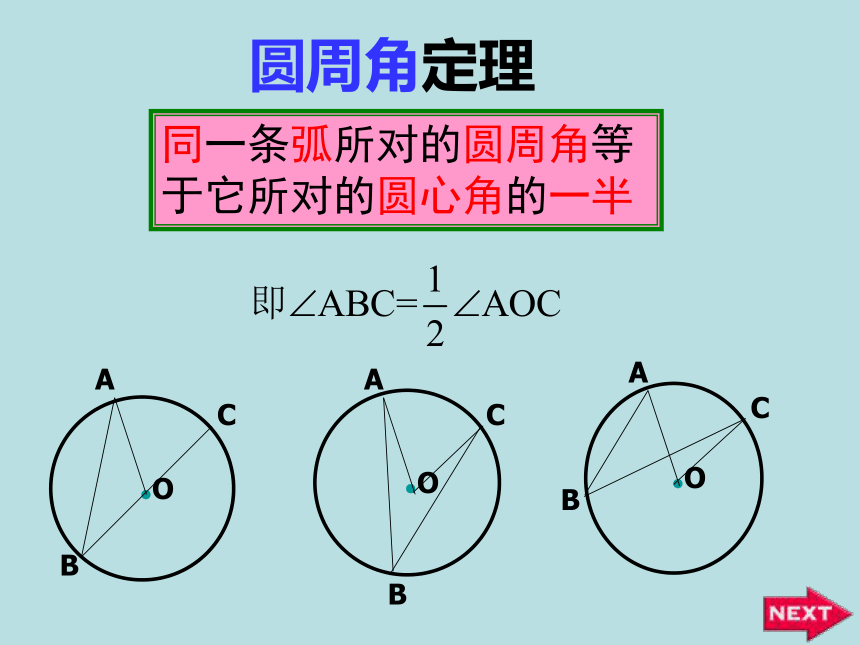
它所对的圆心角的一半.试一试圆周角定理同一条弧所对的圆周角等
于它所对的圆心角的一半1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5做一做····100°AO20°O90°ABABBCOBACC(1)(2)(3)(4)AB为直径,求∠ACB求∠AOB求∠AOB求∠A做一做如图 .已知圆心角∠AOB的度数为100°.求圆周角∠ACB的度数.AOBC做一做2.如图.在⊙O中.∠BOC=50°,求∠BAC 的大小.BOCA1.举出生活中含有圆周角的例子.随堂练习习题证明:∠ACB= ∠AOB12∠BAC= ∠BOC2∠AOB=2∠BOC∠ACB=2∠BAC1 规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理分析:2再见明港二中王玲圆周角和圆心角的关系第二课时1.什么是圆周角?顶点在圆上,它的两边分别与圆还有另一个交点,像这样的角,叫做圆周角.忆一忆2.圆周角定理的内容是什么?一条弧所对的圆周角等于它所对的圆心角的一半.B
100o50o36o或144o64o100o做一做1.100o的弧所对的圆心角等于_______,所对的圆周角等于_______
2、一弦分圆周成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为______________
3、如图,在⊙O中,∠BAC=32o,则∠BOC=______
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______1.如图1,在⊙O中,∠ABC,∠ADC,∠AEC有什么共同特征?它们的大小有什么关系?为什么?议一议∠ABC = ∠ADC = ∠AEC2.如图2,在⊙O中,若弧AB等于弧EF.能否得到∠C =∠G呢?议一议3.如图,BC是⊙O的直径,你知道它所对的圆周角的大小吗?图3议一议∠BAC =90o4.如图4,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?议一议圆周角定理的推论1同圆或等圆中,同弧或等弧所对的圆周角相等用于找相等的弧或角
圆周角定理的推论2直径所对的圆周角是直角
90°圆周角所对的弦是直径用于判断某条直线是否过圆心
或判断某个圆周角是否是直角例 如图.AB是⊙O的直径.BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?BCAD解:BD=CD∵AB是⊙O的直径理由是:连接AD试一试∴BD=CD又∵AC=AB即AD⊥BC∴ ∠ADB= 90o ·o(1)当船与两个灯塔的夹角∠α大于
“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小
于“危险角”时,船位于哪个区域?
为什么?做一做船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁.如图所示,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁. ·o答(1)船位于暗礁区域内(即圆o内).
理由:假设船在⊙O上,则有∠α=∠C,这与
∠α> ∠ C矛盾.所以船不可能在⊙O上;
假设船在⊙O外,则有∠ α< ∠AEB,即
∠ α < ∠C,这与∠ α > ∠C矛盾.
所以:
船不可能在⊙O外.
因此,船只能位于⊙O内.(2)船位于暗礁区域外(即⊙O外).2. 如图,哪个角与∠BAC 相等?1.为什么有些电影院的坐位排列(横排)呈圆弧形?说一说这种设计的合理性?随堂练习3.如图.⊙O的直径AB=10cm,C是⊙O上的一点.
∠ABC =30°.求AC的长.随堂练习解:AB是直径∴ ∠ACB= 90o即:AC = 5cm∵∠ABC= 30°∴AC= AB4.小明想用直角尺检查某些工件是否恰好为半圆形. 根据下图, 你能判断哪个是半圆形吗?为什么?随堂练习习题1.在如图所示的8个角中,哪些是相等的角?你能从图中找出几对相似三角形吗?2.你能设法确定一个圆形纸片的圆心吗? 有几种方法?我手中有一个量角器和一个直角三角尺,你用什么方法可以确定量角器是半圆形? 想一想ABCD(1)(2).O.OABCCD.O.OABCD(3) 1.在⊙o中,与∠BAC相等的角有( ).2.如图,在⊙O中,四边形ABCD的对角线把四个内角
分成的八个角中有( ) 相等的角.
3.如图,在⊙O中,直径AB=10㎝, ∠BAC=30°,则
AC=( ) ㎝.∠BDC四对练一练5.如图,AB是⊙O的直径,∠ACD=15°,求∠BAD的大小.AOBCD练一练如图,圆O中,AB是直径,半径CO⊥ AB,D是CO的中点,DE // AB,求:∠EBA练一练再见谢谢指导
要理解并掌握这个模型试一试②当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否转化为①的情况?过点B作直径BD.由①可得:∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.试一试③当圆心(O)在圆周角(∠ABC)的外部时,圆周
角∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否也转化为①的情况?
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于
它所对的圆心角的一半.试一试圆周角定理同一条弧所对的圆周角等
于它所对的圆心角的一半1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5做一做····100°AO20°O90°ABABBCOBACC(1)(2)(3)(4)AB为直径,求∠ACB求∠AOB求∠AOB求∠A做一做如图 .已知圆心角∠AOB的度数为100°.求圆周角∠ACB的度数.AOBC做一做2.如图.在⊙O中.∠BOC=50°,求∠BAC 的大小.BOCA1.举出生活中含有圆周角的例子.随堂练习习题证明:∠ACB= ∠AOB12∠BAC= ∠BOC2∠AOB=2∠BOC∠ACB=2∠BAC1 规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理分析:2再见明港二中王玲圆周角和圆心角的关系第二课时1.什么是圆周角?顶点在圆上,它的两边分别与圆还有另一个交点,像这样的角,叫做圆周角.忆一忆2.圆周角定理的内容是什么?一条弧所对的圆周角等于它所对的圆心角的一半.B
100o50o36o或144o64o100o做一做1.100o的弧所对的圆心角等于_______,所对的圆周角等于_______
2、一弦分圆周成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为______________
3、如图,在⊙O中,∠BAC=32o,则∠BOC=______
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______1.如图1,在⊙O中,∠ABC,∠ADC,∠AEC有什么共同特征?它们的大小有什么关系?为什么?议一议∠ABC = ∠ADC = ∠AEC2.如图2,在⊙O中,若弧AB等于弧EF.能否得到∠C =∠G呢?议一议3.如图,BC是⊙O的直径,你知道它所对的圆周角的大小吗?图3议一议∠BAC =90o4.如图4,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?议一议圆周角定理的推论1同圆或等圆中,同弧或等弧所对的圆周角相等用于找相等的弧或角
圆周角定理的推论2直径所对的圆周角是直角
90°圆周角所对的弦是直径用于判断某条直线是否过圆心
或判断某个圆周角是否是直角例 如图.AB是⊙O的直径.BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?BCAD解:BD=CD∵AB是⊙O的直径理由是:连接AD试一试∴BD=CD又∵AC=AB即AD⊥BC∴ ∠ADB= 90o ·o(1)当船与两个灯塔的夹角∠α大于
“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小
于“危险角”时,船位于哪个区域?
为什么?做一做船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁.如图所示,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁. ·o答(1)船位于暗礁区域内(即圆o内).
理由:假设船在⊙O上,则有∠α=∠C,这与
∠α> ∠ C矛盾.所以船不可能在⊙O上;
假设船在⊙O外,则有∠ α< ∠AEB,即
∠ α < ∠C,这与∠ α > ∠C矛盾.
所以:
船不可能在⊙O外.
因此,船只能位于⊙O内.(2)船位于暗礁区域外(即⊙O外).2. 如图,哪个角与∠BAC 相等?1.为什么有些电影院的坐位排列(横排)呈圆弧形?说一说这种设计的合理性?随堂练习3.如图.⊙O的直径AB=10cm,C是⊙O上的一点.
∠ABC =30°.求AC的长.随堂练习解:AB是直径∴ ∠ACB= 90o即:AC = 5cm∵∠ABC= 30°∴AC= AB4.小明想用直角尺检查某些工件是否恰好为半圆形. 根据下图, 你能判断哪个是半圆形吗?为什么?随堂练习习题1.在如图所示的8个角中,哪些是相等的角?你能从图中找出几对相似三角形吗?2.你能设法确定一个圆形纸片的圆心吗? 有几种方法?我手中有一个量角器和一个直角三角尺,你用什么方法可以确定量角器是半圆形? 想一想ABCD(1)(2).O.OABCCD.O.OABCD(3) 1.在⊙o中,与∠BAC相等的角有( ).2.如图,在⊙O中,四边形ABCD的对角线把四个内角
分成的八个角中有( ) 相等的角.
3.如图,在⊙O中,直径AB=10㎝, ∠BAC=30°,则
AC=( ) ㎝.∠BDC四对练一练5.如图,AB是⊙O的直径,∠ACD=15°,求∠BAD的大小.AOBCD练一练如图,圆O中,AB是直径,半径CO⊥ AB,D是CO的中点,DE // AB,求:∠EBA练一练再见谢谢指导
