圆测试卷[上学期]
图片预览



文档简介
圆
一、选择题
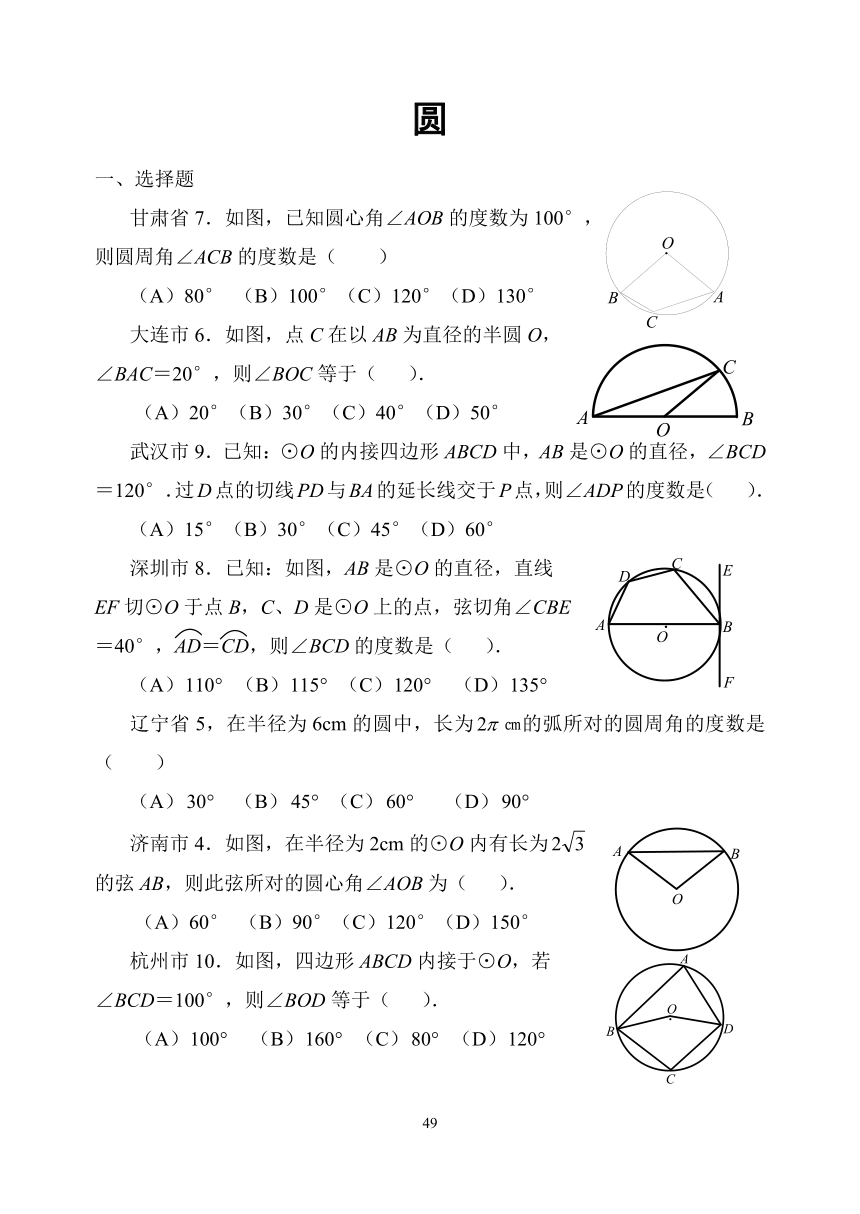
甘肃省7.如图,已知圆心角∠AOB的度数为100°,
则圆周角∠ACB的度数是( )
(A)80° (B)100°(C)120°(D)130°
大连市6.如图,点C在以AB为直径的半圆O,
∠BAC=20°,则∠BOC等于( ).
(A)20°(B)30°(C)40°(D)50°
武汉市9.已知:⊙O的内接四边形ABCD中,AB是⊙O的直径,∠BCD=120°.过D点的切线PD与BA的延长线交于P点,则∠ADP的度数是( ).
(A)15°(B)30°(C)45°(D)60°
深圳市8.已知:如图,AB是⊙O的直径,直线
EF切⊙O于点B,C、D是⊙O上的点,弦切角∠CBE
=40°,AD=CD,则∠BCD的度数是( ).
(A) (B) (C) (D)
辽宁省5,在半径为6cm的圆中,长为㎝的弧所对的圆周角的度数是( )
(A) (B) (C) (D)
济南市4.如图,在半径为2cm的⊙O内有长为
的弦AB,则此弦所对的圆心角∠AOB为( ).
(A)60° (B)90°(C)120°(D)150°
杭州市10.如图,四边形ABCD内接于⊙O,若
∠BCD=100°,则∠BOD等于( ).
(A) (B) (C) (D)
杭州市15.如图,已知⊙O的半径为5,两弦AB、
CD相交于AB的中点E,且AB=8,CE:ED=
4:9,则圆心到弦CD的距离为( ).
(A) (B) (C) (D)
北京市东城区6.已知:如图,AB是⊙O的弦,半
径OC⊥AB于点D,且AB=8cm, O=5cm,则DC的
长为( ).
(A)3cm(B)2.5cm(C)2cm(D)1cm
武汉市10.已知:圆内接四边形ABCD中,对角线AC⊥BD,AB>CD.若CD=4,则AB的弦心距为( ).
(A) (B)2 (C) (D)
苏州市19.如图,在△ABC中,∠C=90°,
AB=10,AC=6,以AC为直径作圆与斜边交于
点P,则BP的长为( ).
(A) (B) (C) (D)
济南市14.如图,直线AB经过⊙O的圆心,与⊙O
相交于A、B两点,点C在⊙O上,且∠AOC=30°.
点E是直线AB上的一个动点(与点O不重合),直线
EC交⊙O于D,则使DE=DO的点E共有( ).
(A)l个 (B)2个 (C)3个 (D)4个
山西16.如果正多边形的一个内角是144°,则这个多边形是( ).
(A)正十边形 (B)正九边形 (C)正八边形 (D)正七边形
杭州市8.如图,一正方形同时外切和内接于两
个同心圆,当小圆的半径为r时,大圆的半径应为
( ).
(A) (B) (C) (D)
天津18.已知正三角形的边长为a,其内切圆的半径为r,外接圆的半径为R,则r:a:R等于( ).
(A) (B) (C) (D)
黑龙江省20.如图,将半径为2的圆形纸片,
沿半径OA、OB将其裁成1:3两部分,用所得
的扇形围成圆锥的侧面,则圆锥的底面半径为( ).
(A) (B)1 (C) 或3 (D)或
南昌市16.如图,⊙A、⊙B、⊙C两两不
相交,且它们的半径都是0.5cm,则图中三个
扇形(即三个阴影部分)的面积之和为( ).
(A) (B) (C) (D)
南京市14.1994年版人民币一角硬币正面图案中有一个正九边形,如果这个正九边形的半径是R,那么它的边长是( ).
(A)(B)(C)(D)
哈尔滨市10.如图,AB、CD是⊙O的直径,
⊙O的半径为R,AB⊥CD,以B为圆心,以BC
为半径作CED,则CED与CAD围成的新月形
ACED的面积为( )平方单位.
(A) (B) (C) (D)
吉林省19.如图,同心圆中,两圆半径分别为2、l,
∠AOB=120°,则阴影部分的面积为( ).
(A)(B)(C)(D)
南京市12.将三角形绕直线l旋转一周,可以得到图所示的立体图形的
是( ).
(A) (B) (C) (D)
二、填空题
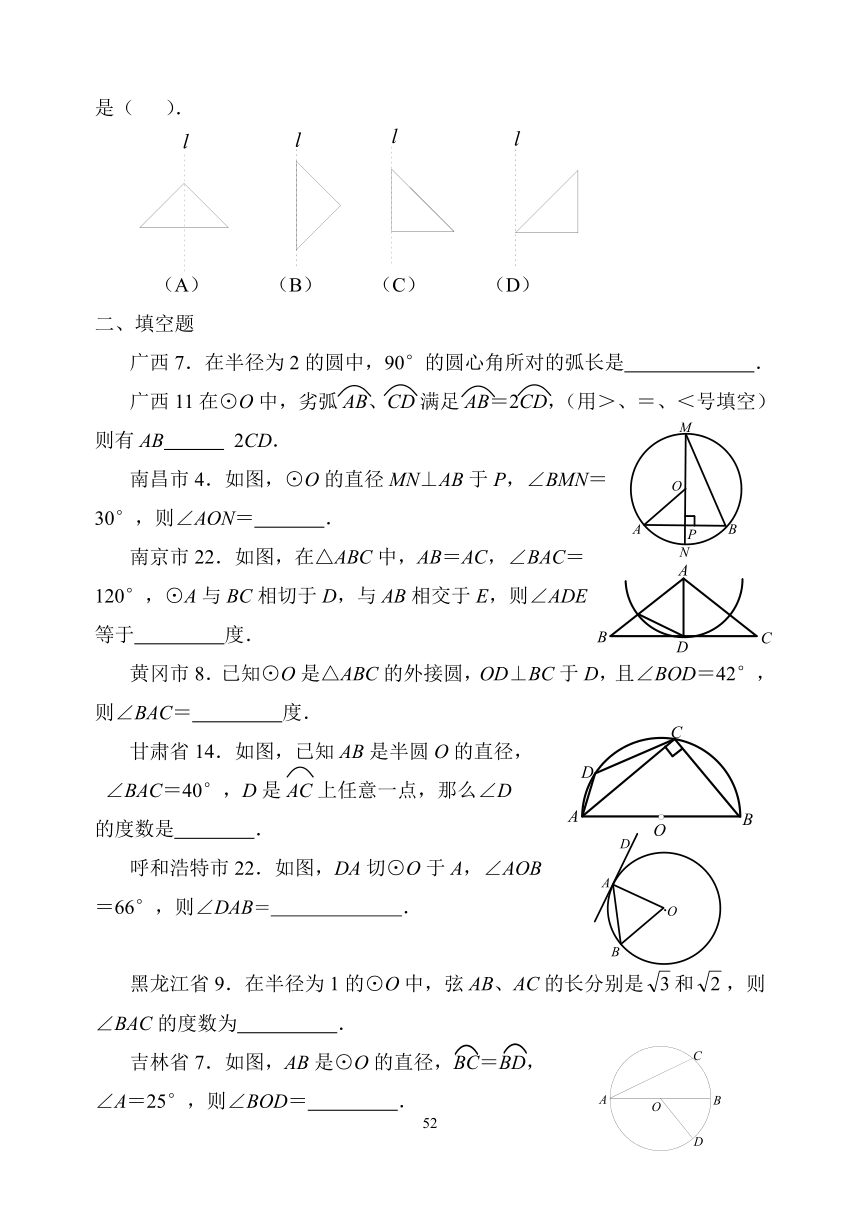
广西7.在半径为2的圆中,90°的圆心角所对的弧长是 .
广西11在⊙O中,劣弧AB、CD满足AB=2CD,(用>、=、<号填空)则有AB 2CD.
南昌市4.如图,⊙O的直径MN⊥AB于P,∠BMN=
30°,则∠AON= .
南京市22.如图,在△ABC中,AB=AC,∠BAC=
120°,⊙A与BC相切于D,与AB相交于E,则∠ADE
等于 度.
黄冈市8.已知⊙O是△ABC的外接圆,OD⊥BC于D,且∠BOD=42°,则∠BAC= 度.
甘肃省14.如图,已知AB是半圆O的直径,
∠BAC=40°,D是AC上任意一点,那么∠D
的度数是 .
呼和浩特市22.如图,DA切⊙O于A,∠AOB
=66°,则∠DAB= .
黑龙江省9.在半径为1的⊙O中,弦AB、AC的长分别是和,则∠BAC的度数为 .
吉林省7.如图,AB是⊙O的直径,BC=BD,
∠A=25°,则∠BOD= .
吉林省13.如图,⊙O的直径为10弦AB=8,
P是弦AB上的一个动点,那么OP长的取值范围
是 .
深圳市12.如图,⊙O的直径AB=10cm,C
是⊙O上一点,点D平分BC,DE=2cm,则弦
AC= .
河北省6.若三角形的三边长分别为3、4、5,则其外接圆直径的长等于 .
山西10.三角形的一边长为a,它的对角为30°,则此三角形外接圆的半径为 .
大连市13.若正三角形的边长为2,则这个正三角形的面积为 平方单位.
长沙市10.如图,PA、PB是⊙O的两条
切线,A、B为切点,直线OP交⊙O于点D、
E,交AB于C.图中互相垂直的线段有
⊥
(只要写出一对线段).
重庆市19.已知:如图,PT切⊙O于点T,PA
交⊙O于A、B两点且与直径CT交于点D,
CD=2,AD=3, BD=6,则PB= .
河北省7.如图,AB是⊙O的弦,AC切⊙O于点A,
且∠BAC=45°,AB=2,则⊙O的面积为 .
(结果可保留).
山西9.如图,AB与⊙O相切于点B,割线ACD交
⊙O于C、D两点,已知AC=1,AC:CD=1:4,则
AB的长等于 .
南昌市5.如图,⊙O中,两弦AB与CD相
交于点P,且PA:PB=3:2,PC=8cm,PD=
3cm,则PA= cm,AB= cm.
辽宁省16.已知:如图,⊙O的弦AB平分
弦CD,AB=10,CD=8,且PA<PB,则PB-
PA= .
四川省6.如图,PT是⊙O的切线,T为切
点,PA是割线,交⊙O于A、B两点,与直径
CT交于点D.已知CD=2,AD=3,BD=4,那
么PB= .
哈尔滨市20.如图,从圆外一点P引圆的
切线PA,点A为切点,割线PDB交⊙O于点D、
B,已知PA=12,PD=8,则
.
福州市12.如图,两个同心圆,过大圆上一点A
作小圆的割线交小圆于B、C两点,且,
则图中圆环的面积为 .
厦门市26.如图,⊙O和⊙相交于A和B,
PQ切⊙O于P,交⊙于Q和M交AB的延长
线于N,MN=3,QN=15,则 PN= .
河南省15.半径为1的两个等圆⊙与⊙外离,且两条内公切线互相垂直,那么圆心距= ,内公切线与外公切线的夹角为 .
辽宁省17.半径分别为3cm和4cm的两圆,一条内公切线长为7cm,则这条内公切线与连心线所夹锐角的度数为 .
大连市II卷5.(6分)半径为1和2的两圆的圆心距为4,则它们的外公切线与连心线所夹锐角的正弦值为 ,内公切线长为 .
安徽10.⊙、⊙和⊙是三个半径为1的等圆,且圆心在同一条直线上.若⊙分别与⊙、⊙相交,⊙与⊙不相交,则⊙与⊙的圆心距d的取值范围是 .
甘肃省17.半径为4的两个等圆,它们的内公切线互相垂直,则这两圆的圆心距等于 .
武汉市15.⊙和⊙交于A、B两点,且⊙经过点,若∠AB=90°,那么∠AB的度数是 .
四川省4.用一个半径为30cm,圆心角为120°的
扇形纸片如图,做成一个圆锥模型的侧面(不计接缝),
那么这个圆锥底面的半径是 cm.
河南省12.已知圆的面积为,其圆周上一段弧长为,那么这段弧所对圆心角的度数是 .
大连市14.如图,圆锥的底面半径OA=3cm,高
SO=4cm,则它的侧面积为 cm.
大连市II卷6.(6分)如图,正方形ABCD的边
长为2,分别以AB、BC为直径在正方形内作半圆,
则图中阴影部分的面积为 平方单位.
武汉市16.如图,AB是⊙的直径,A是⊙
的直径,弦 MN//AB,且MN与⊙相切于C
点,若⊙的半径为2,则B、BN、CN、
C所围成的阴影部分的面积是 .
厦门市28.如图,AB=2cm,∠AOB=90°,
OA=OB,以OA为半径作弧AB,以AB为直径
做半圆AmB,则半圆和弧AB所围成的阴影部分面积是 .
北京市东城区16.如图,⊙O的半径为1,
圆周角∠ABC=30°,则图中阴影部分的面积
是 (结果用表示).
辽宁省22.(5分)已知:如图,P是⊙O外
一点,PA切⊙O于A,AB是⊙O的直径,PB交
⊙O于C,PA=2cm,PC=1cm,求图中阴影部分
的面积S.
大连市II卷3.(6分)如图,△ABC内接于
⊙O.D是劣弧AB上一点,E是BC延长线上一
点,AE交⊙O于F.为使△ADB∽△ACE,应补
充的一个条件是 ,或 .
三、解答题
河南省26.(6分)如图,△ABC中,∠A的平
分线交BC于D,圆O过点A且与BC相切于D,
与AB、AC分别相交于E、F,AD与EF相交于C,
求证:.
呼和浩特市28.如图,AB是△ABC外接圆O
的直径,D为⊙O上一点,且DE⊥CD交BC于E,
求证:.
甘肃省28.(7分)如图,⊙O与⊙A相交于C、
D两点,A点在⊙O上,过A点的直线与CD、
⊙A、⊙O分别交于F、E、B.
求证:.
天津25.(8分)如图,P是⊙O外一点,PD为
切线,D为切点,割线PEF经过圆心O,若PF=
12,PD=.求∠EFD的度数.
河北省23.(8分)如图,⊙O表示一个圆形
工件,图中标注了有关尺寸,并且MB:MA=1:4.
求工件半径的长.
甘肃省29.(7分)如图,已知矩形ABCD中,
AB=1cm,BC=2cm,以B为圆心,BC为半径作
圆弧交AD于F,交BA的延长线于E,求扇形
BCE被矩形所截剩余部分的面积.
青岛市19.工人张师傅要在如图所示的钝角
三角形铁片上截取一个面积最大的半圆形工件,
如果要求半圆形工件的直径恰好在三角形铁片的
最长边上.请你帮助张师傅在右面的三角形铁片
的示意图上,画出符合条件的半圆形工件的示意图.
杭州市26.(l2分)如图,⊙O与⊙外切
于点T,PT为其内公切线,AB为其外公切线,
且A,B为切点,AB与TP相交于点P.根据图
中所给出的已知条件及线段,请写出一个正确结论,并加以证明.
南昌市20.(7分)如图, AB是⊙O的直径,CD切
⊙O于E,AC⊥CD于C,BD⊥CD于D,交⊙O于F.
连结AE、EF.
(1)求证:AE是∠BAC的平分线.
(2)若∠ABD=60°,问:AB与EF是否平行?
长沙市26.如图,△ABC中,AB=AC,D在BC
边上.若DF⊥AB,垂足为F,DG⊥AC,垂足为G,
且DF=DG.
(l)求证:AD⊥BC;
(2)画出△ABC的外接圆,设BE是外接圆直径.求证:.
河南省28.(8分)如图,⊙O的两条割线AB、
AC分别交圆O于 D、B、E、C,弦DF//AC交 BC
于C.
(1)求证:;
(2)若CF=AE.求证:△ABC为等腰三角形.
北京23.(10分)如图,△ABC内接于⊙O,AB是⊙O的直径,PA是过A点的直线,∠PAC=∠B.
(l)求证:PA是⊙O的切线;
(2)如果弦CD交AB于E,CD的延长线交
PA于F,AC=8,CE:ED=6:5,AE:EB=2:3,
求AB的长和∠ECB的正切值.
上海24.(l0分)如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC
于点D,E为AB上的一点,DE=DC,以D为圆心,
DB长为半径作⊙D,
求证:(l)AC是⊙D的切线;
(2)AB+EB=AC.
陕西26.(8分)如图,⊙、⊙外切于
点A,外公切线BC与⊙切于点B,与⊙
切于点C,与的延长线交于点P,已知
.
(l)求⊙、⊙半径的比;
(2)若⊙半径为2㎝,求AB、AC及外公切线BC所围成的图形(阴影部分)的面积.
陕西27.(8分)如图,点I是△ABC的内心,
AI的延长线交边BC于点D,交△ABC外接圆于
点E.
(1)求证:IE=BE;
(2)若IE=4,AE=8,求DE的长.
江西23(9分)如图, ⊙;与⊙相交于
A、B两点,AC切⊙于点A,交⊙于点C;
BD切⊙于点B,交⊙于点D连结 AB、
AD、BC.
(1)求证:;
(2)若∠C=∠D,问四边形ABCD是什么四边形?请加以证明.
大连市II卷10.(14分)如图,梯形ABCD
内接于⊙O,AD//BC,过B引⊙O的切线分别交
DA,CA的延长线于E、F.
(1)求证:;
(2)已知BC=8, CD=5, AF=6,求EF的长
黄冈市18.(l0分)已知:如图,⊙;和⊙
内切于点P,过点P的直线交⊙于点D,交⊙
于点E;DA与⊙相切,切点为C.
(1)求证:PC平分∠APD;
(2)若PE=3,PA=6,求PC的长.
苏州市33.( 6分)如图1、2,已知
AB为半圆O的直径, AP为过点A的半
圆的切线.在AB上任取一点C(点C与
A、 B不重合),过点C作半圆的切线CD
交AP于点D;过点C作CE⊥AB,垂足为E.连结BD,交CE于点F.
(l)当点C为AB的中点时(如图1),求证:CF=EF;
(2)当点C不是AB的中点时(如图2),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
黑龙江省26.(8分)如图,以等腰△ABC的一
腰AB为直径的⊙O交BC于D,过D作DE⊥AC于
E,可得结论:DE是⊙O的切线.
问:(1)若点O在AB上向点B移动,以O为
圆心,OB长为半径的圆仍交BC于D,DE⊥AC
的条件不变,那么上述结论是否还成立?请说明理由;
(2)如果AB=AC=5㎝,,那么圆心O在AB的什么位置时,
⊙O与AC相切?
北京市东城区23.(8分)已知:如图,AB
是半圆O的直径,C为AB上一点,AC为半圆
的直径,BD切半圆于点D, CE⊥AB交
半圆O于点E.
(1)求证: BD=BE;
(2)若两圆半径的比为3:2,试判断∠EBD是直角、锐角还是钝角?并给出证明.
厦门市33.(8分)如图,AB是⊙O的直径,
⊙O交BC于D,过D作⊙O的切线DE交AC于
E,且DE⊥AC.
(1)求证:D是BC的中点;
(2)已知:CD=8, CE=6.4,点为弦AD上的动点,以为圆心,以1为半径的⊙与⊙O有怎样的位置关系?请说明理由.
吉林省29.(8分)如图,矩形ABCD,AD=8,
DC=6,在对角线AC上取一点O,以OC为半径
的圆切AD于E,交BC于F,交CD于C.
(1)求⊙O的半径R;
(2)设∠BFE=,∠CED=,请写出,,90°三者之间的关系
式(只需写出一个),并证明你的结论.
济南市29.(6分)如图1,已知□PQRS是
⊙O的内接四边形.
(1)求证:□PQRS是矩形.
(2)如图2,如果将题目中的⊙O改为边
长为a的正方形ABCD,在AB、AD上分别取点
P、S,连结PS,将Rt△SAP绕正方形中心O旋
转180°得Rt△OCR,从而得四边形PQRS.试
判断四边形PQRS能否变化成矩形?若能,设
PA=x,SA=y,请说明x、y具有什么关系时,四边形PQRS是矩形;若不能,请说明理由.
陕西24.(7分)已知△ABC内接于⊙O.
(1)当点O与AB有怎样的位置关系时,∠ACB是直角;
(2)在满足(1)的条件下,过点C作直线交AB于D,当CD与AB有什么样的关系时,△ABC∽△CBD∽△ACD;
(3)画出符合(l)、(2)题意的两种图形,使图形中的CD=2 cm.
江西26.(11分)如图,正方形ABCD中,有一
直径为BC的半圆,BC=2cm.现有两点E、F,分别
从点B、点A同时出发,点E沿线段BA以1cm/s的
速度向点A运动,点F沿折线A-D-C以2cm/s的
速度向点C运动.设点E离开点B的时间为t(秒).
(l)当t为何值时,线段EF与BC平行?
(2)设1<t<2,当t为何值时,EF与半圆相切?
(3)当 l≤t< 2时,设 EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,请给予证明,并求AP:PC的值.
广西29.(l0分)如图,AB是⊙O的直径,以OA
为直径的⊙;与⊙O的弦AC相交于D, DE⊥
OC,垂足为E.
(l)求证: AD=DC;
(2)求证: DE是⊙的切线;
(3)如果OE=EC,请判断四边形OED是什么四边形,并证明你的结论.
福州市27.(10分)不过圆心的直线l交⊙O于C、D两点,AB是⊙O的直径,AE⊥l,垂足为E,BF⊥l,垂足为F.
(1)在图中的三个圆中分别补画出满足上述条件的具有不同位置关系的图形;
(2)请你观察(l)中所画图形,写出一个各图都具有的两条线段相等的结论(不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程);
(3)请你选择(l)中的一个图形,证明(2)所得出的结论.
济南市30.(8分)如图1,已知⊙O和⊙都经过点A和点B,直线PQ切⊙O于点P,交⊙于点Q、M,交AB的延长线于点N.
(1)求证:.
(2)若M是PQ的中点,设MQ=x,MN=y,求证:x= 3y.
(3)若⊙不动,把⊙O向右或向左平移,分别得到图2、图3、图4,请你判断(直接写出判断结论,不需证明):
①(l)题结论是否仍然成立?
②在图1中,(2)题结论是否仍然成立?在图3、图4中,若将(2)题条件改为:M是PN的中点,设MQ=x, MN=y,则x= 3y的结论是否仍然成立?
辽宁省29.(l0分)已知:如图1,⊙与
⊙相交于A、B两点,经过A点的直线分别
交⊙、⊙于C、D两点(C、D不与B重
合).连结BD,过C作BD的平行线交⊙于
点E,连结BE.
(l)求证:BE是⊙的切线;
(2)如图2,若两圆圆心在公共弦AB的同侧,
其他条件不变,判断BE和⊙的位置关系;
(不要求证明)
(3)若点C为劣弧AB的中点,其他条件
不变,连结AB、AE,AB与CE交于点F,如
图3写出图中所有的相似三角形.(不另外连
线,不要求证明)
济南市31.(9分)如图,等边△ABC的边
长为,以BC边所在直线为x轴,BC边上
的高线AO所在的直线为y轴建立平面直角坐
标系.
(l)求过A、B、C三点的抛物线的解析式.
(2)如图,设⊙P是△ABC的内切圆,分别切AB、AC于E、F点,求阴影部分的面积.
(3)点D为y轴上一动点,当以D点为圆心,3为半径的⊙D与直线AB、AC都相切时,试判断⊙D与(2)中⊙P的位置关系,并简要说明理由.
(4)若(2)中⊙P的大小不变,圆心P沿y轴运动,设P点坐标为(0,a),则⊙P与直线AB、AC有几种位置关系?并写出相应位置关系时a的取值范围.
PAGE
64
一、选择题
甘肃省7.如图,已知圆心角∠AOB的度数为100°,
则圆周角∠ACB的度数是( )
(A)80° (B)100°(C)120°(D)130°
大连市6.如图,点C在以AB为直径的半圆O,
∠BAC=20°,则∠BOC等于( ).
(A)20°(B)30°(C)40°(D)50°
武汉市9.已知:⊙O的内接四边形ABCD中,AB是⊙O的直径,∠BCD=120°.过D点的切线PD与BA的延长线交于P点,则∠ADP的度数是( ).
(A)15°(B)30°(C)45°(D)60°
深圳市8.已知:如图,AB是⊙O的直径,直线
EF切⊙O于点B,C、D是⊙O上的点,弦切角∠CBE
=40°,AD=CD,则∠BCD的度数是( ).
(A) (B) (C) (D)
辽宁省5,在半径为6cm的圆中,长为㎝的弧所对的圆周角的度数是( )
(A) (B) (C) (D)
济南市4.如图,在半径为2cm的⊙O内有长为
的弦AB,则此弦所对的圆心角∠AOB为( ).
(A)60° (B)90°(C)120°(D)150°
杭州市10.如图,四边形ABCD内接于⊙O,若
∠BCD=100°,则∠BOD等于( ).
(A) (B) (C) (D)
杭州市15.如图,已知⊙O的半径为5,两弦AB、
CD相交于AB的中点E,且AB=8,CE:ED=
4:9,则圆心到弦CD的距离为( ).
(A) (B) (C) (D)
北京市东城区6.已知:如图,AB是⊙O的弦,半
径OC⊥AB于点D,且AB=8cm, O=5cm,则DC的
长为( ).
(A)3cm(B)2.5cm(C)2cm(D)1cm
武汉市10.已知:圆内接四边形ABCD中,对角线AC⊥BD,AB>CD.若CD=4,则AB的弦心距为( ).
(A) (B)2 (C) (D)
苏州市19.如图,在△ABC中,∠C=90°,
AB=10,AC=6,以AC为直径作圆与斜边交于
点P,则BP的长为( ).
(A) (B) (C) (D)
济南市14.如图,直线AB经过⊙O的圆心,与⊙O
相交于A、B两点,点C在⊙O上,且∠AOC=30°.
点E是直线AB上的一个动点(与点O不重合),直线
EC交⊙O于D,则使DE=DO的点E共有( ).
(A)l个 (B)2个 (C)3个 (D)4个
山西16.如果正多边形的一个内角是144°,则这个多边形是( ).
(A)正十边形 (B)正九边形 (C)正八边形 (D)正七边形
杭州市8.如图,一正方形同时外切和内接于两
个同心圆,当小圆的半径为r时,大圆的半径应为
( ).
(A) (B) (C) (D)
天津18.已知正三角形的边长为a,其内切圆的半径为r,外接圆的半径为R,则r:a:R等于( ).
(A) (B) (C) (D)
黑龙江省20.如图,将半径为2的圆形纸片,
沿半径OA、OB将其裁成1:3两部分,用所得
的扇形围成圆锥的侧面,则圆锥的底面半径为( ).
(A) (B)1 (C) 或3 (D)或
南昌市16.如图,⊙A、⊙B、⊙C两两不
相交,且它们的半径都是0.5cm,则图中三个
扇形(即三个阴影部分)的面积之和为( ).
(A) (B) (C) (D)
南京市14.1994年版人民币一角硬币正面图案中有一个正九边形,如果这个正九边形的半径是R,那么它的边长是( ).
(A)(B)(C)(D)
哈尔滨市10.如图,AB、CD是⊙O的直径,
⊙O的半径为R,AB⊥CD,以B为圆心,以BC
为半径作CED,则CED与CAD围成的新月形
ACED的面积为( )平方单位.
(A) (B) (C) (D)
吉林省19.如图,同心圆中,两圆半径分别为2、l,
∠AOB=120°,则阴影部分的面积为( ).
(A)(B)(C)(D)
南京市12.将三角形绕直线l旋转一周,可以得到图所示的立体图形的
是( ).
(A) (B) (C) (D)
二、填空题
广西7.在半径为2的圆中,90°的圆心角所对的弧长是 .
广西11在⊙O中,劣弧AB、CD满足AB=2CD,(用>、=、<号填空)则有AB 2CD.
南昌市4.如图,⊙O的直径MN⊥AB于P,∠BMN=
30°,则∠AON= .
南京市22.如图,在△ABC中,AB=AC,∠BAC=
120°,⊙A与BC相切于D,与AB相交于E,则∠ADE
等于 度.
黄冈市8.已知⊙O是△ABC的外接圆,OD⊥BC于D,且∠BOD=42°,则∠BAC= 度.
甘肃省14.如图,已知AB是半圆O的直径,
∠BAC=40°,D是AC上任意一点,那么∠D
的度数是 .
呼和浩特市22.如图,DA切⊙O于A,∠AOB
=66°,则∠DAB= .
黑龙江省9.在半径为1的⊙O中,弦AB、AC的长分别是和,则∠BAC的度数为 .
吉林省7.如图,AB是⊙O的直径,BC=BD,
∠A=25°,则∠BOD= .
吉林省13.如图,⊙O的直径为10弦AB=8,
P是弦AB上的一个动点,那么OP长的取值范围
是 .
深圳市12.如图,⊙O的直径AB=10cm,C
是⊙O上一点,点D平分BC,DE=2cm,则弦
AC= .
河北省6.若三角形的三边长分别为3、4、5,则其外接圆直径的长等于 .
山西10.三角形的一边长为a,它的对角为30°,则此三角形外接圆的半径为 .
大连市13.若正三角形的边长为2,则这个正三角形的面积为 平方单位.
长沙市10.如图,PA、PB是⊙O的两条
切线,A、B为切点,直线OP交⊙O于点D、
E,交AB于C.图中互相垂直的线段有
⊥
(只要写出一对线段).
重庆市19.已知:如图,PT切⊙O于点T,PA
交⊙O于A、B两点且与直径CT交于点D,
CD=2,AD=3, BD=6,则PB= .
河北省7.如图,AB是⊙O的弦,AC切⊙O于点A,
且∠BAC=45°,AB=2,则⊙O的面积为 .
(结果可保留).
山西9.如图,AB与⊙O相切于点B,割线ACD交
⊙O于C、D两点,已知AC=1,AC:CD=1:4,则
AB的长等于 .
南昌市5.如图,⊙O中,两弦AB与CD相
交于点P,且PA:PB=3:2,PC=8cm,PD=
3cm,则PA= cm,AB= cm.
辽宁省16.已知:如图,⊙O的弦AB平分
弦CD,AB=10,CD=8,且PA<PB,则PB-
PA= .
四川省6.如图,PT是⊙O的切线,T为切
点,PA是割线,交⊙O于A、B两点,与直径
CT交于点D.已知CD=2,AD=3,BD=4,那
么PB= .
哈尔滨市20.如图,从圆外一点P引圆的
切线PA,点A为切点,割线PDB交⊙O于点D、
B,已知PA=12,PD=8,则
.
福州市12.如图,两个同心圆,过大圆上一点A
作小圆的割线交小圆于B、C两点,且,
则图中圆环的面积为 .
厦门市26.如图,⊙O和⊙相交于A和B,
PQ切⊙O于P,交⊙于Q和M交AB的延长
线于N,MN=3,QN=15,则 PN= .
河南省15.半径为1的两个等圆⊙与⊙外离,且两条内公切线互相垂直,那么圆心距= ,内公切线与外公切线的夹角为 .
辽宁省17.半径分别为3cm和4cm的两圆,一条内公切线长为7cm,则这条内公切线与连心线所夹锐角的度数为 .
大连市II卷5.(6分)半径为1和2的两圆的圆心距为4,则它们的外公切线与连心线所夹锐角的正弦值为 ,内公切线长为 .
安徽10.⊙、⊙和⊙是三个半径为1的等圆,且圆心在同一条直线上.若⊙分别与⊙、⊙相交,⊙与⊙不相交,则⊙与⊙的圆心距d的取值范围是 .
甘肃省17.半径为4的两个等圆,它们的内公切线互相垂直,则这两圆的圆心距等于 .
武汉市15.⊙和⊙交于A、B两点,且⊙经过点,若∠AB=90°,那么∠AB的度数是 .
四川省4.用一个半径为30cm,圆心角为120°的
扇形纸片如图,做成一个圆锥模型的侧面(不计接缝),
那么这个圆锥底面的半径是 cm.
河南省12.已知圆的面积为,其圆周上一段弧长为,那么这段弧所对圆心角的度数是 .
大连市14.如图,圆锥的底面半径OA=3cm,高
SO=4cm,则它的侧面积为 cm.
大连市II卷6.(6分)如图,正方形ABCD的边
长为2,分别以AB、BC为直径在正方形内作半圆,
则图中阴影部分的面积为 平方单位.
武汉市16.如图,AB是⊙的直径,A是⊙
的直径,弦 MN//AB,且MN与⊙相切于C
点,若⊙的半径为2,则B、BN、CN、
C所围成的阴影部分的面积是 .
厦门市28.如图,AB=2cm,∠AOB=90°,
OA=OB,以OA为半径作弧AB,以AB为直径
做半圆AmB,则半圆和弧AB所围成的阴影部分面积是 .
北京市东城区16.如图,⊙O的半径为1,
圆周角∠ABC=30°,则图中阴影部分的面积
是 (结果用表示).
辽宁省22.(5分)已知:如图,P是⊙O外
一点,PA切⊙O于A,AB是⊙O的直径,PB交
⊙O于C,PA=2cm,PC=1cm,求图中阴影部分
的面积S.
大连市II卷3.(6分)如图,△ABC内接于
⊙O.D是劣弧AB上一点,E是BC延长线上一
点,AE交⊙O于F.为使△ADB∽△ACE,应补
充的一个条件是 ,或 .
三、解答题
河南省26.(6分)如图,△ABC中,∠A的平
分线交BC于D,圆O过点A且与BC相切于D,
与AB、AC分别相交于E、F,AD与EF相交于C,
求证:.
呼和浩特市28.如图,AB是△ABC外接圆O
的直径,D为⊙O上一点,且DE⊥CD交BC于E,
求证:.
甘肃省28.(7分)如图,⊙O与⊙A相交于C、
D两点,A点在⊙O上,过A点的直线与CD、
⊙A、⊙O分别交于F、E、B.
求证:.
天津25.(8分)如图,P是⊙O外一点,PD为
切线,D为切点,割线PEF经过圆心O,若PF=
12,PD=.求∠EFD的度数.
河北省23.(8分)如图,⊙O表示一个圆形
工件,图中标注了有关尺寸,并且MB:MA=1:4.
求工件半径的长.
甘肃省29.(7分)如图,已知矩形ABCD中,
AB=1cm,BC=2cm,以B为圆心,BC为半径作
圆弧交AD于F,交BA的延长线于E,求扇形
BCE被矩形所截剩余部分的面积.
青岛市19.工人张师傅要在如图所示的钝角
三角形铁片上截取一个面积最大的半圆形工件,
如果要求半圆形工件的直径恰好在三角形铁片的
最长边上.请你帮助张师傅在右面的三角形铁片
的示意图上,画出符合条件的半圆形工件的示意图.
杭州市26.(l2分)如图,⊙O与⊙外切
于点T,PT为其内公切线,AB为其外公切线,
且A,B为切点,AB与TP相交于点P.根据图
中所给出的已知条件及线段,请写出一个正确结论,并加以证明.
南昌市20.(7分)如图, AB是⊙O的直径,CD切
⊙O于E,AC⊥CD于C,BD⊥CD于D,交⊙O于F.
连结AE、EF.
(1)求证:AE是∠BAC的平分线.
(2)若∠ABD=60°,问:AB与EF是否平行?
长沙市26.如图,△ABC中,AB=AC,D在BC
边上.若DF⊥AB,垂足为F,DG⊥AC,垂足为G,
且DF=DG.
(l)求证:AD⊥BC;
(2)画出△ABC的外接圆,设BE是外接圆直径.求证:.
河南省28.(8分)如图,⊙O的两条割线AB、
AC分别交圆O于 D、B、E、C,弦DF//AC交 BC
于C.
(1)求证:;
(2)若CF=AE.求证:△ABC为等腰三角形.
北京23.(10分)如图,△ABC内接于⊙O,AB是⊙O的直径,PA是过A点的直线,∠PAC=∠B.
(l)求证:PA是⊙O的切线;
(2)如果弦CD交AB于E,CD的延长线交
PA于F,AC=8,CE:ED=6:5,AE:EB=2:3,
求AB的长和∠ECB的正切值.
上海24.(l0分)如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC
于点D,E为AB上的一点,DE=DC,以D为圆心,
DB长为半径作⊙D,
求证:(l)AC是⊙D的切线;
(2)AB+EB=AC.
陕西26.(8分)如图,⊙、⊙外切于
点A,外公切线BC与⊙切于点B,与⊙
切于点C,与的延长线交于点P,已知
.
(l)求⊙、⊙半径的比;
(2)若⊙半径为2㎝,求AB、AC及外公切线BC所围成的图形(阴影部分)的面积.
陕西27.(8分)如图,点I是△ABC的内心,
AI的延长线交边BC于点D,交△ABC外接圆于
点E.
(1)求证:IE=BE;
(2)若IE=4,AE=8,求DE的长.
江西23(9分)如图, ⊙;与⊙相交于
A、B两点,AC切⊙于点A,交⊙于点C;
BD切⊙于点B,交⊙于点D连结 AB、
AD、BC.
(1)求证:;
(2)若∠C=∠D,问四边形ABCD是什么四边形?请加以证明.
大连市II卷10.(14分)如图,梯形ABCD
内接于⊙O,AD//BC,过B引⊙O的切线分别交
DA,CA的延长线于E、F.
(1)求证:;
(2)已知BC=8, CD=5, AF=6,求EF的长
黄冈市18.(l0分)已知:如图,⊙;和⊙
内切于点P,过点P的直线交⊙于点D,交⊙
于点E;DA与⊙相切,切点为C.
(1)求证:PC平分∠APD;
(2)若PE=3,PA=6,求PC的长.
苏州市33.( 6分)如图1、2,已知
AB为半圆O的直径, AP为过点A的半
圆的切线.在AB上任取一点C(点C与
A、 B不重合),过点C作半圆的切线CD
交AP于点D;过点C作CE⊥AB,垂足为E.连结BD,交CE于点F.
(l)当点C为AB的中点时(如图1),求证:CF=EF;
(2)当点C不是AB的中点时(如图2),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
黑龙江省26.(8分)如图,以等腰△ABC的一
腰AB为直径的⊙O交BC于D,过D作DE⊥AC于
E,可得结论:DE是⊙O的切线.
问:(1)若点O在AB上向点B移动,以O为
圆心,OB长为半径的圆仍交BC于D,DE⊥AC
的条件不变,那么上述结论是否还成立?请说明理由;
(2)如果AB=AC=5㎝,,那么圆心O在AB的什么位置时,
⊙O与AC相切?
北京市东城区23.(8分)已知:如图,AB
是半圆O的直径,C为AB上一点,AC为半圆
的直径,BD切半圆于点D, CE⊥AB交
半圆O于点E.
(1)求证: BD=BE;
(2)若两圆半径的比为3:2,试判断∠EBD是直角、锐角还是钝角?并给出证明.
厦门市33.(8分)如图,AB是⊙O的直径,
⊙O交BC于D,过D作⊙O的切线DE交AC于
E,且DE⊥AC.
(1)求证:D是BC的中点;
(2)已知:CD=8, CE=6.4,点为弦AD上的动点,以为圆心,以1为半径的⊙与⊙O有怎样的位置关系?请说明理由.
吉林省29.(8分)如图,矩形ABCD,AD=8,
DC=6,在对角线AC上取一点O,以OC为半径
的圆切AD于E,交BC于F,交CD于C.
(1)求⊙O的半径R;
(2)设∠BFE=,∠CED=,请写出,,90°三者之间的关系
式(只需写出一个),并证明你的结论.
济南市29.(6分)如图1,已知□PQRS是
⊙O的内接四边形.
(1)求证:□PQRS是矩形.
(2)如图2,如果将题目中的⊙O改为边
长为a的正方形ABCD,在AB、AD上分别取点
P、S,连结PS,将Rt△SAP绕正方形中心O旋
转180°得Rt△OCR,从而得四边形PQRS.试
判断四边形PQRS能否变化成矩形?若能,设
PA=x,SA=y,请说明x、y具有什么关系时,四边形PQRS是矩形;若不能,请说明理由.
陕西24.(7分)已知△ABC内接于⊙O.
(1)当点O与AB有怎样的位置关系时,∠ACB是直角;
(2)在满足(1)的条件下,过点C作直线交AB于D,当CD与AB有什么样的关系时,△ABC∽△CBD∽△ACD;
(3)画出符合(l)、(2)题意的两种图形,使图形中的CD=2 cm.
江西26.(11分)如图,正方形ABCD中,有一
直径为BC的半圆,BC=2cm.现有两点E、F,分别
从点B、点A同时出发,点E沿线段BA以1cm/s的
速度向点A运动,点F沿折线A-D-C以2cm/s的
速度向点C运动.设点E离开点B的时间为t(秒).
(l)当t为何值时,线段EF与BC平行?
(2)设1<t<2,当t为何值时,EF与半圆相切?
(3)当 l≤t< 2时,设 EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,请给予证明,并求AP:PC的值.
广西29.(l0分)如图,AB是⊙O的直径,以OA
为直径的⊙;与⊙O的弦AC相交于D, DE⊥
OC,垂足为E.
(l)求证: AD=DC;
(2)求证: DE是⊙的切线;
(3)如果OE=EC,请判断四边形OED是什么四边形,并证明你的结论.
福州市27.(10分)不过圆心的直线l交⊙O于C、D两点,AB是⊙O的直径,AE⊥l,垂足为E,BF⊥l,垂足为F.
(1)在图中的三个圆中分别补画出满足上述条件的具有不同位置关系的图形;
(2)请你观察(l)中所画图形,写出一个各图都具有的两条线段相等的结论(不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程);
(3)请你选择(l)中的一个图形,证明(2)所得出的结论.
济南市30.(8分)如图1,已知⊙O和⊙都经过点A和点B,直线PQ切⊙O于点P,交⊙于点Q、M,交AB的延长线于点N.
(1)求证:.
(2)若M是PQ的中点,设MQ=x,MN=y,求证:x= 3y.
(3)若⊙不动,把⊙O向右或向左平移,分别得到图2、图3、图4,请你判断(直接写出判断结论,不需证明):
①(l)题结论是否仍然成立?
②在图1中,(2)题结论是否仍然成立?在图3、图4中,若将(2)题条件改为:M是PN的中点,设MQ=x, MN=y,则x= 3y的结论是否仍然成立?
辽宁省29.(l0分)已知:如图1,⊙与
⊙相交于A、B两点,经过A点的直线分别
交⊙、⊙于C、D两点(C、D不与B重
合).连结BD,过C作BD的平行线交⊙于
点E,连结BE.
(l)求证:BE是⊙的切线;
(2)如图2,若两圆圆心在公共弦AB的同侧,
其他条件不变,判断BE和⊙的位置关系;
(不要求证明)
(3)若点C为劣弧AB的中点,其他条件
不变,连结AB、AE,AB与CE交于点F,如
图3写出图中所有的相似三角形.(不另外连
线,不要求证明)
济南市31.(9分)如图,等边△ABC的边
长为,以BC边所在直线为x轴,BC边上
的高线AO所在的直线为y轴建立平面直角坐
标系.
(l)求过A、B、C三点的抛物线的解析式.
(2)如图,设⊙P是△ABC的内切圆,分别切AB、AC于E、F点,求阴影部分的面积.
(3)点D为y轴上一动点,当以D点为圆心,3为半径的⊙D与直线AB、AC都相切时,试判断⊙D与(2)中⊙P的位置关系,并简要说明理由.
(4)若(2)中⊙P的大小不变,圆心P沿y轴运动,设P点坐标为(0,a),则⊙P与直线AB、AC有几种位置关系?并写出相应位置关系时a的取值范围.
PAGE
64
