4.6圆和圆的位置关系课件

课件22张PPT。九年级数学(上)第四章： 对圆的进一步认识 【学习目标】
1.经历探索两个圆之间位置关系的过程；了解圆与圆之间的几种位置关系.
2.了解两圆外切、内切时两圆圆心距d、半径R和r之间的数量关系.
重点： 两圆外切、内切时两圆圆心距d、半径R和r的数量关系.
难点：以两圆位置关系为背景的几何题的多种情况讨论.奥运会会徽日全食按钮 观察图片 活动 一活动 二
1、亲自动手实验实验步骤与目的:
在两张透明纸上画出两个半径不同的圆，把两张纸叠合在一起，固定其中一张
而移动另一张，请观察圆与圆有几种位置关系？你能画出几种不同的位置关系
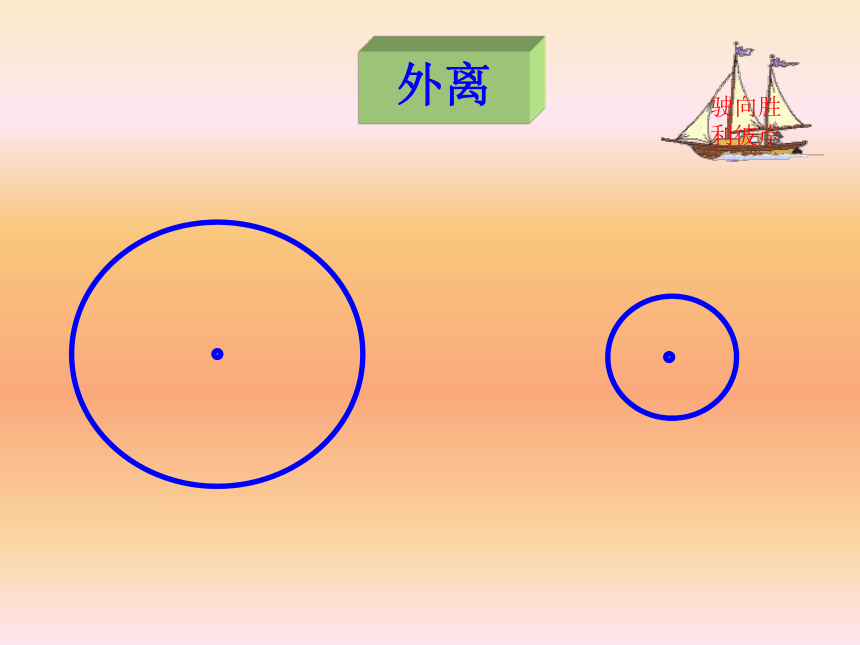
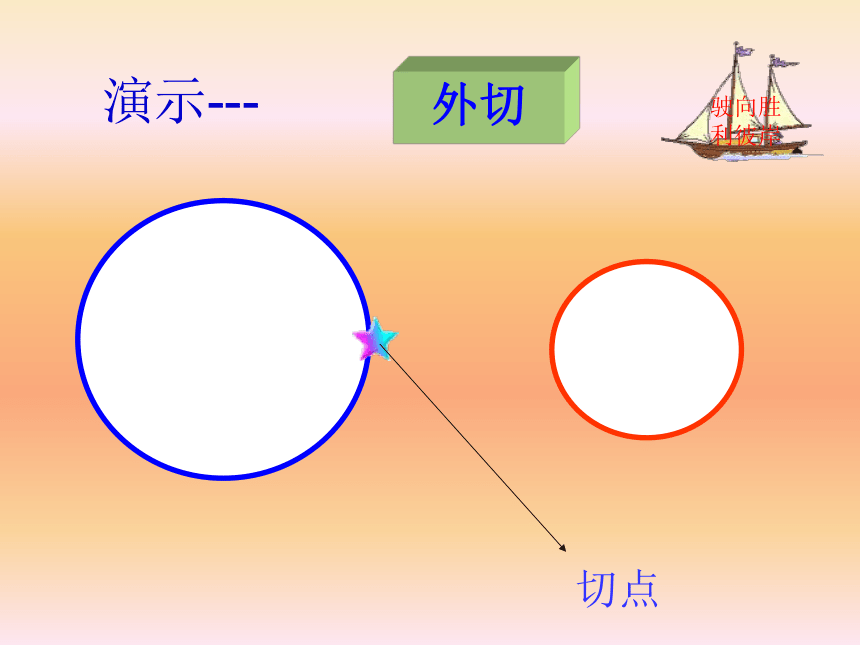
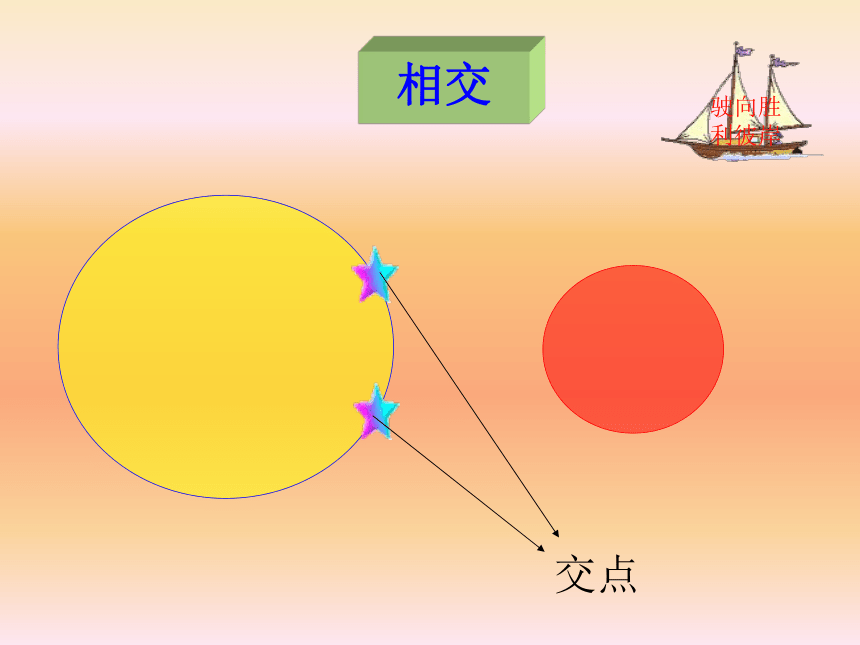
吗？每种位置关系中两圆有多少公共点？2、演示圆与圆相对运动外离外切演示---切点相交交点内切切点内含同心圆 相 离 相 切 相 交外离内含外切内切你能再举出一些表示生活中两圆不同的位置关系实例吗？活动三活动四定理探索演示发现规律1、两圆的位置关系与半径和差有关R-r
内切R+r
外切口决：和差切，交中间，内含外离在两边内含相交外离 ⊙01和⊙02的半径分别为3cm和4cm,设
(1) 0102=8cm (2) 0102=7cm
(3) 0102=5cm (4) 0102=1cm
(5) 0102=0.5cm (6) 01和02重合
⊙0和⊙02的位置关系怎样?
练习

(2)两圆外切 (3)两圆相交 (4)两圆内切 (5)两圆内含 (6)两圆同心答: (1)两圆相离2.已知⊙O1与⊙O2的半径分别为5cm和3cm，圆心距020=7cm，
则两圆的位置关系为（ ）
A．外离 B．外切 C．相交 D．内切
3、已知两圆半径分别为2和3，圆心距为 d，若两圆没有公共点，
则下列结论正确的是（ ）
A． B．
C． 或 D． 或
4、已知⊙O1的半径为3cm，⊙O2的半径为4cm，
两圆的圆心距O1O2为7cm，则⊙O1与⊙O2的位置关系是 ．
5、已知⊙O1和⊙O2的半径分别是一元二次方程
的两根，且O1O2=2则⊙O1和⊙O2的位置关系是 ．cD 例:如图⊙O的半径为4cm，点P是⊙O外一点,OP=6cm
求：(1)以P为圆心作⊙P与⊙O外切，小圆⊙P 的半径是多少?
(2)以P为圆心作⊙P与⊙O内切，大圆⊙P的半径是多少?
解：(1)设⊙O与⊙P外切
于点A，则 PA=OP-OA
∴ PA=2 cm(2)设⊙O与⊙P内切
于点B，则 PB=OP+OB
∴ PB=10 cm.请看课本：以P为圆心作⊙P与⊙O相切？定圆0的半径是4cm,动圆P的半径是1cm,
(1) 设⊙ P和⊙ 0相外切,那么点P与点O的距离
是多少?点P可以在什么样的线上运动
(2) 设⊙ P 和 ⊙O 相内切,情况又怎样?
(1) 解:∵⊙0和⊙P相外切
∴OP＝ R + r
∴OP=5cm
∴ P点在以O点为圆心,以5cm
为半径的圆上运动讨论思考 (2) 解: ∵⊙0和⊙P相内切
∴ OP=R-r
∴OP=3cm
∴ P点在以O点为圆心,以3cm
为半径的圆上运动课堂小结
外离外切相交内切内含01210d>R+r
d=R+r
R-r圆的外部一圆在另一
圆的外部两圆相交一圆在另一
圆的内部一圆在另一
圆的内部名称当堂达标
1、两个圆的半径为3cm和5cm，圆心距是2cm，则两圆的位置
关系是（ ）
A．外切 B．相交 C．内切 D．内含
2、⊙O1 的圆心坐标为（2，0），半径为1，⊙O2的圆心坐标为
（-1，0），半径为3，则这两圆的位置关系是（ ）
相交 B. 相切 C.相离 D.内含
3、半径分别为1cm和5cm的两圆相交，则圆心距d的取值范围
是（ ）
d <6 B.4< d<6 C. 4≤d<6 D. 1 4、 已知两圆⊙O1、⊙O2相切，⊙O1的半径是3cm，
⊙O2的半径是2cm，求两圆的圆心距。
布置作业1、将例题增加一问：以点P为圆心，作圆P与圆O外离，相交或内含，圆P的半径各是多少？

2、将讨论作变式训练： ⊙O1半径为2，⊙O2半径为1，如果⊙O1固定，⊙O2 绕⊙O1滚动一周，且⊙O2不停自转，当⊙O2回到原来位置,⊙O2转了几周？谢谢！如果你在空中建造了楼阁，你的努力
便不应迷失方向，楼阁原本在哪里，
你就应在它的下面打牢基础。