河北省衡水市2022-2023学年九年级下学期第二次月考数学试卷(含答案)
文档属性
| 名称 | 河北省衡水市2022-2023学年九年级下学期第二次月考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 930.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 16:17:10 | ||
图片预览




文档简介
2023年河北省初中毕业生升学文化课考试
数学模拟试卷(三)
本试卷共12页.总分120分,考试时间120分钟.
一、选择题(本大题共16个小题,1~10小题每题3分,11~16小题每题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.与的结果相等的是( )
A.的倒数 B.的0次幂
C.1的立方根 D.的平方
2.如图,将木条a,b与木条c钉在一起,与∠1构成内错角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
3.下列各式中,计算结果是的是( )
A. B. C. D.
4.2022年中国空间站完成在轨建造,中国空间站绕地球飞行的速度约为m/s,则中国空间站绕地球飞行s走过的路程(m)用科学记数法可表示为( )
A. B. C. D.
5.如图,点C,D在直线AB上,则的度数为( )
A.95° B.105° C.115° D.125°
6.如图是由6个正方体组成的几何体,下列几何体(由与图3中同等大小的正方体组成)中,其三视图的总面积与图几何体三视图的总面积相等的是( )
A. B. C. D.
7.如图是嘉琪进行分式计算的过程,下列判断不正确的是( )
A.第二步运用了分式的基本性质 B.从第三步开始出现错误
C.原分式的计算结果 D.当时,原分式的值为0
8.如图1,某长方体A,B,C三个面的面积之比是,当A,B,C三个面分别接触地面时,水平地面所受压强分别为,,.已知满足的函数图象如图2所示,其中p是压强,F是压力(物体放在水平地面上,物体对地面的压力等于该物体的重力),S是受力面积,则,,的大小关系为( )
图1 图2
A. B. C. D.
9.五个正整数由小到大的排列顺序是x,y,4,5,5,若这组数据唯一的众数是5,则的最大值是( )
A.4 B.5 C.6 D.8
10.下列是4位同学所画的菱形,依据所标数据,不一定为菱形的是( )
A. B. C. D.
11.小明利用平面直角坐标系画出来的某公园景区地图如图所示,若湖心亭B、游乐园D的坐标分别为,,则距离原点O最远的景点是( )
A.燕赵之光A B.湖心亭B C.望春亭C D.游乐园D
12.如图,在数轴上从左到右依次有A,B,C三点,若,点A表示的数为a,点C表示的数为,则线段BC的长为( )
A. B. C. D.
13.课本习题:“某超市的一种瓶装饮料每箱售价为36元,元旦期间对该瓶装饮料进行促销活动,买一箱送两瓶,这相当于每瓶按原价的九折销售,求这家超市销售这种饮料的原价是每瓶多少元及该饮料每箱多少瓶?”下列是四位同学列出的方程,正确的是( )
甲:解:设该饮料的原价是每瓶x元,则.
乙:解:设该饮料的原价是每瓶x元,则.
丙:解:设该饮料每箱y瓶,则.
丁:解:设该饮料每箱y瓶,则.
A.甲和丙 B.甲和丁 C.乙和丙 D.乙和丁
14.把一根铁丝首尾相接围成一个长为3cm,宽为2cm的矩形,要将它按如图所示的方式向外扩张得到矩形,使矩形矩形,则这根铁丝需增加( )
A.3.5cm B.5cm C.7cm D.10cm
15.如图,直角三角形PAB的一条边为AB,另一顶点P在直线l上,下面是三位学生作直角三角形的过程以及自认为正确的最终结论,下列判断正确的是( )
甲:过点A作直线l的垂线,垂足为;过点B作直线l的垂线,垂足为,故符合题意的点P有两处;
乙:以AB为直径作,与直线l交于,两点,故符合题意的点P有两处;
丙:过点A作,与直线l交于点;过点B作,与直线l交于点,故符合题意的点P有两处
A.甲的作法和结论均正确
B.甲、乙的作法和结论合在一起才正确图9
C.乙、丙的作法和结论合在一起才正确
D.乙的作法和结论均不正确
16.如图,在中,,P是线段BC外一动点,,连接CP,将线段CP绕点P逆时针旋转90°得到线段DP,连接BD,CD,下列判断正确的是( )
结论Ⅰ:当点P落在线段BD上时,BD的长为7;
结论Ⅱ:BD长度的最大值为.
A.结论Ⅰ、Ⅱ都对 B.结论Ⅰ、Ⅱ都不对
C.只有结论Ⅰ对 D.只有结论Ⅱ对
二、填空题(本大题共3个小题,每小题3分,共9分.其中18小题第一空2分,第二空1分;19小题每空1分)
17.有a,b,c三条绳子穿过一片木板,姐妹两人分别站在木板的左、右两边(两人彼此都看不见),各选该边的一条绳子,若姐姐先选中了绳子a,则妹妹与姐姐选到同一条绳子的概率为__________.
18.如图,将12cm长的铁丝围成的正三角形,再重新依次围成正六边形、正十二形、正二十四边形等.
(1)铁丝重新围成的正六边形外接圆的周长为__________cm;
(2)铁丝重新围成的正六边形的面积__________(填“>”“<”或“=”)铁丝重新围成的正十二边形的面积.(提示:,)
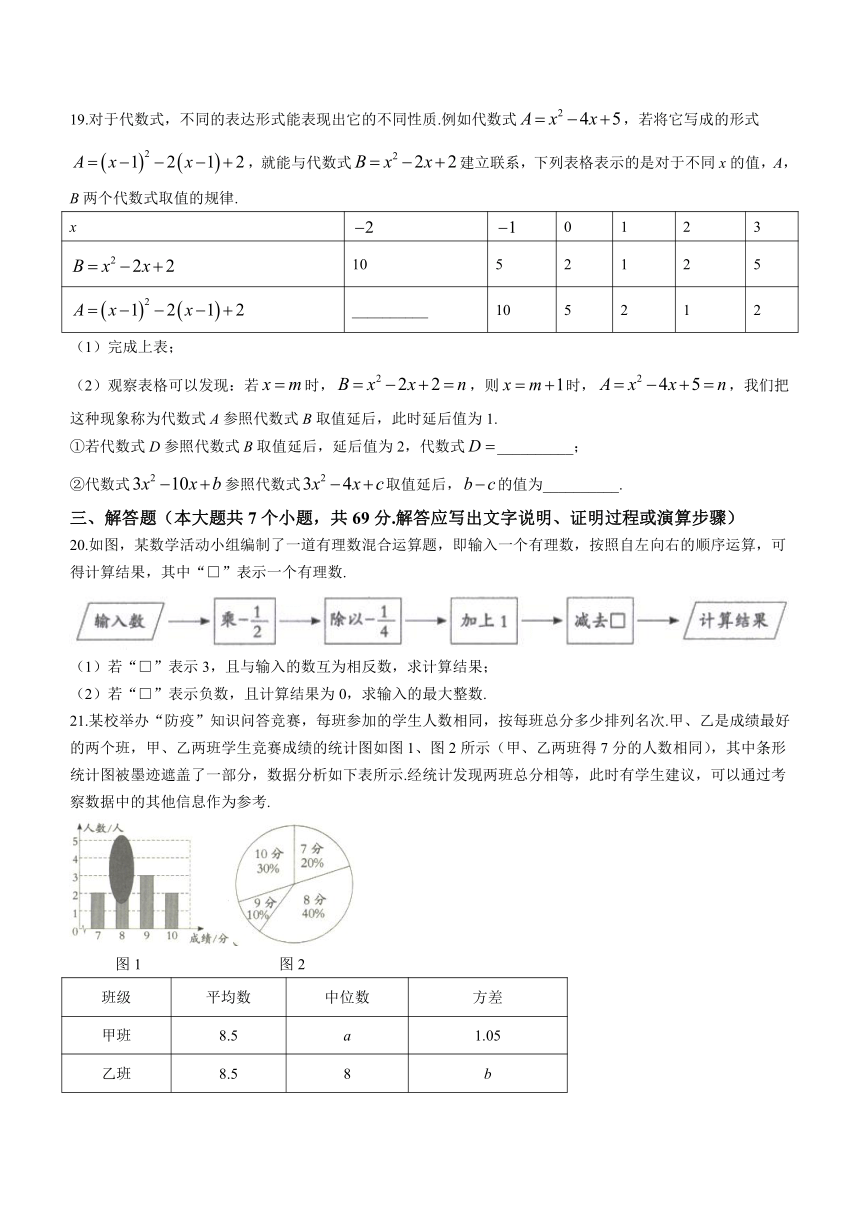
19.对于代数式,不同的表达形式能表现出它的不同性质.例如代数式,若将它写成的形式,就能与代数式建立联系,下列表格表示的是对于不同x的值,A,B两个代数式取值的规律.
x 0 1 2 3
10 5 2 1 2 5
__________ 10 5 2 1 2
(1)完成上表;
(2)观察表格可以发现:若时,,则时,,我们把这种现象称为代数式A参照代数式B取值延后,此时延后值为1.
①若代数式D参照代数式B取值延后,延后值为2,代数式__________;
②代数式参照代数式取值延后,的值为__________.
三、解答题(本大题共7个小题,共69分.解答应写出文字说明、证明过程或演算步骤)
20.如图,某数学活动小组编制了一道有理数混合运算题,即输入一个有理数,按照自左向右的顺序运算,可得计算结果,其中“□”表示一个有理数.
(1)若“□”表示3,且与输入的数互为相反数,求计算结果;
(2)若“□”表示负数,且计算结果为0,求输入的最大整数.
21.某校举办“防疫”知识问答竞赛,每班参加的学生人数相同,按每班总分多少排列名次.甲、乙是成绩最好的两个班,甲、乙两班学生竞赛成绩的统计图如图1、图2所示(甲、乙两班得7分的人数相同),其中条形统计图被墨迹遮盖了一部分,数据分析如下表所示.经统计发现两班总分相等,此时有学生建议,可以通过考察数据中的其他信息作为参考.
图1 图2
班级 平均数 中位数 方差
甲班 8.5 a 1.05
乙班 8.5 8 b
注:方差
(1)求条形统计图中被遮盖的数;
(2)求出表中a,b的值;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
22.问题情景:将下列完全平方式进行因式分解,将结果直接写在横线上.
;;__________;
探究发现:观察以上多项式,发现:;;;
归纳猜想:若多项式是完全平方式,则a,b,c之间存在的数量关系为;
验证结论:嘉琪验证归纳猜想中的结论的过程如下,请补全嘉琪的验证过程;
____________________
∵是完全平方式,
∴__________,即.
解决问题:
①若多项式是一个完全平方式,求n的值;
②若多项式加上一个含字母y的单项式就能变形为一个完全平方式,请直接写出所有满足条件的单项式.
23.图1是煤油温度计,该温度计的左侧是华氏温度(℉),右侧是摄氏温度(℃).华氏温度与摄氏温度之间存在着某种函数关系,小明通过查阅资料和观察温度计,得到了如下表所示的数据.
摄氏温度值x/℃ 0 10 20 30 40
华氏温度值y/℉ 32 50 68 86 104
图1 图2
(1)观察表格中的数据,华氏温度与摄氏温度之间的关系是__________(填“一次”、“反比例”或“二次”)函数;在如图2所示的平面直角坐标系中描出上表相应的点,并用平滑的线进行连接;
(2)求y与x之间的函数解析式;
(3)设(1)中所画的图象与直线交于点A,点A的实际意义是__________;
(4)某种疫苗需低温保存,其活性只能在某温度区间(摄氏温度)内维持,在该温度区间内,任意摄氏温度与其对应的华氏温度的数值相差的最大值为16,求该温度区间的最大温差是多少摄氏度.
24.下图是小明家的房间甲和房间乙,他将一个长度可伸缩变化的梯子斜靠在墙上,梯子顶端在墙上的点M处,如果梯子的底端P不动,旋转梯子,使得旋转后梯子顶端靠在对面墙上的点N处,此时.
甲 乙
(1)在甲房间时,小明测得,,,求证:;
(2)在乙房间时,小明测得,,.
①当时,求的长度;
②求乙房间的宽CD(用含c的式子表示).
25.如图,抛物线与直线交于A,B两点(点A在点B的左侧),该抛物线的对称轴是直线.
(1)若点在该抛物线上,求抛物线的解析式;
(2)当,且时,求抛物线的最大值与最小值的差;
(3)已知M是直线AB上的动点,将点M向上平移2个单位长度得到点N,若线段MN与抛物线有公共点,请直接写出点M的横坐标m的取值范围.
26.如图1,在平行四边形中,,,,以AB为直径在AB的上方作半圆O,交AD于点E,P为上一动点(不与点A,B重合),将半圆O沿BP折叠,得到点A的对称点,点O的对称点.
图1 图2
(1)当点在半圆O上时,的度数为__________;
(2)如图2,连接BD,BP与AE交于点F.已知,且.
①求BD的长度及的值;
②求阴影部分的面积;
(3)点P在上运动过程中,当直线DC能与所在的圆相切时,直接写出a的取值范围.
2023年河北省初中毕业生升学文化课考试
数学模拟试卷(三)参考答案
一、(1-10题每题3分,11-16题每题2分,共计42分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
答案 A C D D B B D A B B B D C D C A
16.【精思博考】当点P落在线段BD上时,如图1所示.
∵,∴.
∵,,∴,∴,∴.
连接AD.
∵,∴当点D在BA的延长线上时(如图2所示),BD的长度取得最大值.
由题意可得和都是等腰直角三角形,
∴,∴,即.
∵,,∴,
∴,∴.
∵,∴,∴BD长度的最大值为.
图1 图2
二、(每小题3分,共9分. 其中18小题第一空2分,第二空1分;19小题每空1分)
17.
18.(1);(2)<
19.(1)17;
(2)①(或;②7
19②【精思博考】∵代数式参照代数式取值延后,设延后值为m,
∴,
∴,∴.
∵,∴
三、20.解:(1)根据题意,输入的数为,
∴,即计算结果为;
(2)设输入的数为a,“□”表示的数为b.
根据题意可得,整理得.
∵b是负数,∴,∴,∴输入的最大整数为.
21.解:(1)每班参加竞赛的学生的人数为(人),
∴条形统计图中被遮盖的数为;
(2)甲班的10名学生的比赛成绩由小到大排列为7,7,8,8,8,9,9,9,10,10,
∴甲班的成绩的中位数为,即a的值为8.5.
乙班的10名学生的比赛成绩由小到大排列为7,7,8,8,8,8,9,10,10,10,
∴;
(3)应该把冠军奖状发给甲班;
∵甲班的中位数比乙班大,且甲班的方差比乙班小,
∴甲班的成绩比乙班好,∴应该把冠军奖状发给甲班.
22.解:问题情境;
验证结论;(或);(或);
解决问题①由题意可得,解得;
②所有满足条件的单项式有,或.
23.解:(1)一次;如图;
(2)设y与x的函数解析式为.
将,代入中,解得
∴y与x的函数解析式为;
(3)华氏温度的值与摄氏温度的值相等;
(4)根据题意可得.
当时,解得;当时,解得,(℃),
即该温度区间的最大温差为40℃.
24.解:(1)证明:在中, .
∵,∴,∴.
又∵,,∴,
∴,,∴;
(2)①在中,,∴.
∵,,∴,∴的长度为;
②如图,连接MN,过点N作于点Q,
∴.
∵,,∴是等边三角形,∴,.
∵,∴在中,,∴,
∴,∴.
∵,∴四边形是矩形,∴,即乙房间的宽CD为c.
【②另一种解法:也可证明进行求解】
25.解:(1)∵抛物线过点,对称轴为直线,
∴解得
∴抛物线的解析式为;
(2)当,时,.∵,∴当时,y有最大值3.
当时,结合函数图象,当时,y有最小值-6,
∴抛物线的最大值与最小值的差为;
(3)点M的横坐标m的取值范围为或.
【精思博考】设点N在抛物线上,则,即,解得,.
当,整理得,解得,.
∵点A在点B的左侧,∴点A的横坐标为-1,点B的横坐标为2.
结合图象,当线段MN与抛物线有公共点时,点M的横坐标m的取值范围为或.
26.解:(1)60°;
(2)①如图1,连接,.
∵AB是的直径,∴,根据轴对称的性质,可得.
∵,∴,∴.
∵,,∴,∴.
∵,∴,∴,∴.
∵,∴,
∴在中,由勾股定理可得BD=4.
∵在中,,∴,∴,
∴,即的值为;
②如图1,连接OP,过点P作于点Q.
由①可得,∴,∴,
∴利用轴对称的性质可得;
(3)a的取值范围是.
图1
【精思博考】如图2,
当点P与点A重合时,点D与点E也重合,此时直线CD与相切,
此时a最小,.
∵点P不与点A重合,∴.
如图3,
当点与点D重合时,此时直线DC与所在的圆相切,且a最大,.
综上所述,a的取值范围是.
图2 图3
数学模拟试卷(三)
本试卷共12页.总分120分,考试时间120分钟.
一、选择题(本大题共16个小题,1~10小题每题3分,11~16小题每题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.与的结果相等的是( )
A.的倒数 B.的0次幂
C.1的立方根 D.的平方
2.如图,将木条a,b与木条c钉在一起,与∠1构成内错角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
3.下列各式中,计算结果是的是( )
A. B. C. D.
4.2022年中国空间站完成在轨建造,中国空间站绕地球飞行的速度约为m/s,则中国空间站绕地球飞行s走过的路程(m)用科学记数法可表示为( )
A. B. C. D.
5.如图,点C,D在直线AB上,则的度数为( )
A.95° B.105° C.115° D.125°
6.如图是由6个正方体组成的几何体,下列几何体(由与图3中同等大小的正方体组成)中,其三视图的总面积与图几何体三视图的总面积相等的是( )
A. B. C. D.
7.如图是嘉琪进行分式计算的过程,下列判断不正确的是( )
A.第二步运用了分式的基本性质 B.从第三步开始出现错误
C.原分式的计算结果 D.当时,原分式的值为0
8.如图1,某长方体A,B,C三个面的面积之比是,当A,B,C三个面分别接触地面时,水平地面所受压强分别为,,.已知满足的函数图象如图2所示,其中p是压强,F是压力(物体放在水平地面上,物体对地面的压力等于该物体的重力),S是受力面积,则,,的大小关系为( )
图1 图2
A. B. C. D.
9.五个正整数由小到大的排列顺序是x,y,4,5,5,若这组数据唯一的众数是5,则的最大值是( )
A.4 B.5 C.6 D.8
10.下列是4位同学所画的菱形,依据所标数据,不一定为菱形的是( )
A. B. C. D.
11.小明利用平面直角坐标系画出来的某公园景区地图如图所示,若湖心亭B、游乐园D的坐标分别为,,则距离原点O最远的景点是( )
A.燕赵之光A B.湖心亭B C.望春亭C D.游乐园D
12.如图,在数轴上从左到右依次有A,B,C三点,若,点A表示的数为a,点C表示的数为,则线段BC的长为( )
A. B. C. D.
13.课本习题:“某超市的一种瓶装饮料每箱售价为36元,元旦期间对该瓶装饮料进行促销活动,买一箱送两瓶,这相当于每瓶按原价的九折销售,求这家超市销售这种饮料的原价是每瓶多少元及该饮料每箱多少瓶?”下列是四位同学列出的方程,正确的是( )
甲:解:设该饮料的原价是每瓶x元,则.
乙:解:设该饮料的原价是每瓶x元,则.
丙:解:设该饮料每箱y瓶,则.
丁:解:设该饮料每箱y瓶,则.
A.甲和丙 B.甲和丁 C.乙和丙 D.乙和丁
14.把一根铁丝首尾相接围成一个长为3cm,宽为2cm的矩形,要将它按如图所示的方式向外扩张得到矩形,使矩形矩形,则这根铁丝需增加( )
A.3.5cm B.5cm C.7cm D.10cm
15.如图,直角三角形PAB的一条边为AB,另一顶点P在直线l上,下面是三位学生作直角三角形的过程以及自认为正确的最终结论,下列判断正确的是( )
甲:过点A作直线l的垂线,垂足为;过点B作直线l的垂线,垂足为,故符合题意的点P有两处;
乙:以AB为直径作,与直线l交于,两点,故符合题意的点P有两处;
丙:过点A作,与直线l交于点;过点B作,与直线l交于点,故符合题意的点P有两处
A.甲的作法和结论均正确
B.甲、乙的作法和结论合在一起才正确图9
C.乙、丙的作法和结论合在一起才正确
D.乙的作法和结论均不正确
16.如图,在中,,P是线段BC外一动点,,连接CP,将线段CP绕点P逆时针旋转90°得到线段DP,连接BD,CD,下列判断正确的是( )
结论Ⅰ:当点P落在线段BD上时,BD的长为7;
结论Ⅱ:BD长度的最大值为.
A.结论Ⅰ、Ⅱ都对 B.结论Ⅰ、Ⅱ都不对
C.只有结论Ⅰ对 D.只有结论Ⅱ对
二、填空题(本大题共3个小题,每小题3分,共9分.其中18小题第一空2分,第二空1分;19小题每空1分)
17.有a,b,c三条绳子穿过一片木板,姐妹两人分别站在木板的左、右两边(两人彼此都看不见),各选该边的一条绳子,若姐姐先选中了绳子a,则妹妹与姐姐选到同一条绳子的概率为__________.
18.如图,将12cm长的铁丝围成的正三角形,再重新依次围成正六边形、正十二形、正二十四边形等.
(1)铁丝重新围成的正六边形外接圆的周长为__________cm;
(2)铁丝重新围成的正六边形的面积__________(填“>”“<”或“=”)铁丝重新围成的正十二边形的面积.(提示:,)
19.对于代数式,不同的表达形式能表现出它的不同性质.例如代数式,若将它写成的形式,就能与代数式建立联系,下列表格表示的是对于不同x的值,A,B两个代数式取值的规律.
x 0 1 2 3
10 5 2 1 2 5
__________ 10 5 2 1 2
(1)完成上表;
(2)观察表格可以发现:若时,,则时,,我们把这种现象称为代数式A参照代数式B取值延后,此时延后值为1.
①若代数式D参照代数式B取值延后,延后值为2,代数式__________;
②代数式参照代数式取值延后,的值为__________.
三、解答题(本大题共7个小题,共69分.解答应写出文字说明、证明过程或演算步骤)
20.如图,某数学活动小组编制了一道有理数混合运算题,即输入一个有理数,按照自左向右的顺序运算,可得计算结果,其中“□”表示一个有理数.
(1)若“□”表示3,且与输入的数互为相反数,求计算结果;
(2)若“□”表示负数,且计算结果为0,求输入的最大整数.
21.某校举办“防疫”知识问答竞赛,每班参加的学生人数相同,按每班总分多少排列名次.甲、乙是成绩最好的两个班,甲、乙两班学生竞赛成绩的统计图如图1、图2所示(甲、乙两班得7分的人数相同),其中条形统计图被墨迹遮盖了一部分,数据分析如下表所示.经统计发现两班总分相等,此时有学生建议,可以通过考察数据中的其他信息作为参考.
图1 图2
班级 平均数 中位数 方差
甲班 8.5 a 1.05
乙班 8.5 8 b
注:方差
(1)求条形统计图中被遮盖的数;
(2)求出表中a,b的值;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
22.问题情景:将下列完全平方式进行因式分解,将结果直接写在横线上.
;;__________;
探究发现:观察以上多项式,发现:;;;
归纳猜想:若多项式是完全平方式,则a,b,c之间存在的数量关系为;
验证结论:嘉琪验证归纳猜想中的结论的过程如下,请补全嘉琪的验证过程;
____________________
∵是完全平方式,
∴__________,即.
解决问题:
①若多项式是一个完全平方式,求n的值;
②若多项式加上一个含字母y的单项式就能变形为一个完全平方式,请直接写出所有满足条件的单项式.
23.图1是煤油温度计,该温度计的左侧是华氏温度(℉),右侧是摄氏温度(℃).华氏温度与摄氏温度之间存在着某种函数关系,小明通过查阅资料和观察温度计,得到了如下表所示的数据.
摄氏温度值x/℃ 0 10 20 30 40
华氏温度值y/℉ 32 50 68 86 104
图1 图2
(1)观察表格中的数据,华氏温度与摄氏温度之间的关系是__________(填“一次”、“反比例”或“二次”)函数;在如图2所示的平面直角坐标系中描出上表相应的点,并用平滑的线进行连接;
(2)求y与x之间的函数解析式;
(3)设(1)中所画的图象与直线交于点A,点A的实际意义是__________;
(4)某种疫苗需低温保存,其活性只能在某温度区间(摄氏温度)内维持,在该温度区间内,任意摄氏温度与其对应的华氏温度的数值相差的最大值为16,求该温度区间的最大温差是多少摄氏度.
24.下图是小明家的房间甲和房间乙,他将一个长度可伸缩变化的梯子斜靠在墙上,梯子顶端在墙上的点M处,如果梯子的底端P不动,旋转梯子,使得旋转后梯子顶端靠在对面墙上的点N处,此时.
甲 乙
(1)在甲房间时,小明测得,,,求证:;
(2)在乙房间时,小明测得,,.
①当时,求的长度;
②求乙房间的宽CD(用含c的式子表示).
25.如图,抛物线与直线交于A,B两点(点A在点B的左侧),该抛物线的对称轴是直线.
(1)若点在该抛物线上,求抛物线的解析式;
(2)当,且时,求抛物线的最大值与最小值的差;
(3)已知M是直线AB上的动点,将点M向上平移2个单位长度得到点N,若线段MN与抛物线有公共点,请直接写出点M的横坐标m的取值范围.
26.如图1,在平行四边形中,,,,以AB为直径在AB的上方作半圆O,交AD于点E,P为上一动点(不与点A,B重合),将半圆O沿BP折叠,得到点A的对称点,点O的对称点.
图1 图2
(1)当点在半圆O上时,的度数为__________;
(2)如图2,连接BD,BP与AE交于点F.已知,且.
①求BD的长度及的值;
②求阴影部分的面积;
(3)点P在上运动过程中,当直线DC能与所在的圆相切时,直接写出a的取值范围.
2023年河北省初中毕业生升学文化课考试
数学模拟试卷(三)参考答案
一、(1-10题每题3分,11-16题每题2分,共计42分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
答案 A C D D B B D A B B B D C D C A
16.【精思博考】当点P落在线段BD上时,如图1所示.
∵,∴.
∵,,∴,∴,∴.
连接AD.
∵,∴当点D在BA的延长线上时(如图2所示),BD的长度取得最大值.
由题意可得和都是等腰直角三角形,
∴,∴,即.
∵,,∴,
∴,∴.
∵,∴,∴BD长度的最大值为.
图1 图2
二、(每小题3分,共9分. 其中18小题第一空2分,第二空1分;19小题每空1分)
17.
18.(1);(2)<
19.(1)17;
(2)①(或;②7
19②【精思博考】∵代数式参照代数式取值延后,设延后值为m,
∴,
∴,∴.
∵,∴
三、20.解:(1)根据题意,输入的数为,
∴,即计算结果为;
(2)设输入的数为a,“□”表示的数为b.
根据题意可得,整理得.
∵b是负数,∴,∴,∴输入的最大整数为.
21.解:(1)每班参加竞赛的学生的人数为(人),
∴条形统计图中被遮盖的数为;
(2)甲班的10名学生的比赛成绩由小到大排列为7,7,8,8,8,9,9,9,10,10,
∴甲班的成绩的中位数为,即a的值为8.5.
乙班的10名学生的比赛成绩由小到大排列为7,7,8,8,8,8,9,10,10,10,
∴;
(3)应该把冠军奖状发给甲班;
∵甲班的中位数比乙班大,且甲班的方差比乙班小,
∴甲班的成绩比乙班好,∴应该把冠军奖状发给甲班.
22.解:问题情境;
验证结论;(或);(或);
解决问题①由题意可得,解得;
②所有满足条件的单项式有,或.
23.解:(1)一次;如图;
(2)设y与x的函数解析式为.
将,代入中,解得
∴y与x的函数解析式为;
(3)华氏温度的值与摄氏温度的值相等;
(4)根据题意可得.
当时,解得;当时,解得,(℃),
即该温度区间的最大温差为40℃.
24.解:(1)证明:在中, .
∵,∴,∴.
又∵,,∴,
∴,,∴;
(2)①在中,,∴.
∵,,∴,∴的长度为;
②如图,连接MN,过点N作于点Q,
∴.
∵,,∴是等边三角形,∴,.
∵,∴在中,,∴,
∴,∴.
∵,∴四边形是矩形,∴,即乙房间的宽CD为c.
【②另一种解法:也可证明进行求解】
25.解:(1)∵抛物线过点,对称轴为直线,
∴解得
∴抛物线的解析式为;
(2)当,时,.∵,∴当时,y有最大值3.
当时,结合函数图象,当时,y有最小值-6,
∴抛物线的最大值与最小值的差为;
(3)点M的横坐标m的取值范围为或.
【精思博考】设点N在抛物线上,则,即,解得,.
当,整理得,解得,.
∵点A在点B的左侧,∴点A的横坐标为-1,点B的横坐标为2.
结合图象,当线段MN与抛物线有公共点时,点M的横坐标m的取值范围为或.
26.解:(1)60°;
(2)①如图1,连接,.
∵AB是的直径,∴,根据轴对称的性质,可得.
∵,∴,∴.
∵,,∴,∴.
∵,∴,∴,∴.
∵,∴,
∴在中,由勾股定理可得BD=4.
∵在中,,∴,∴,
∴,即的值为;
②如图1,连接OP,过点P作于点Q.
由①可得,∴,∴,
∴利用轴对称的性质可得;
(3)a的取值范围是.
图1
【精思博考】如图2,
当点P与点A重合时,点D与点E也重合,此时直线CD与相切,
此时a最小,.
∵点P不与点A重合,∴.
如图3,
当点与点D重合时,此时直线DC与所在的圆相切,且a最大,.
综上所述,a的取值范围是.
图2 图3
同课章节目录
